복소수
- 일상적으로 사용하는 대부분 수는 하나의 값으로 표현된다.
- 특이하게 두 개의 값으로 구성되는 수집합이 있다.
- 이를 복소수(Complex number)라고 한다.
- 집합 기호는 C로 표현한다.

- 복소수는 위 그림과 같이 실수(Real number)와 허수(Imaginary number)의 독립된 2개의 요소로 구성된 수집합이다.
허수
- 복소수 체계에서 허수는 실수와 구분된 단위를 가진 특별한 수다.
- 모든 실수는 제곱하면 0보다 크거나 같은 수가 나온다.
- 이러한 실수의 정의만으로 풀리지 않는 문제가 등장하면서 이를 해결하고자 제곱해서 음수가 되는 상상의 수를 고안하였다.
- 이것이 바로 허수다.
- 복소수 체계에서 실수와 허수는 물과 기름과 같이 완전히 분리된 성질을 가진다.
- 이 둘을 구분하기 위해 허수에 i라는 기호를 사용한다.
- 이를 허수 단위(Imaginary unit)라 부른다.
- 허수 단위 i는 제곱했을 때 -1이 나오는 수를 말한다.
i^2 = -1- 복소수 내에서 서로 완전히 분리된 실수 집합과 허수 집합은 각각 실수부(Real part)와 허수 부(Imaginary part)로 부른다.
- 허수부는 항상 i를 사용해 표기
- 즉, 크기가 b인 허수부는 bi로 표기해 실수와 구분한다.
- 실수부의 값이 a이고 허수부의 값이 b인 복소수의 표현 방법
덧셈 기호 사용
a + bi
순서쌍으로 표기
(a, b)복소수의 구조
- 복소수의 덧셈은 실수부와 허수부를 구분해 각각 더해주는 방식을 사용한다.
- 두 복소수의 덧셈은 다음과 같이 전개된다.
(a + bi) + (c + di) = (a + c) + (b + d)i
순서쌍으로 표기
(a, b) + (c, d) = (a + c, b + d)- 복소수의 덧셈 연산이 만족하는 성질은 벡터 덧셈 연산의 성질을 참고해 쉽게 파악할 수 있다.
- 결합법칙 : (a, b) + ((c, d) + (e, f)) = ((a, b) + (c, d)) + (e, f)
- 교환법칙 : (a, b) + (c, d) = (c, d) + (a, b)
- 항등원 : (a, b) + (0, 0) = (a, b)
- 역원 : (a, b) + (-a, -b) = (0, 0)
- 복소수의 곱셈은 모든 요소를 교차해 곱하는 방식으로 동작한다.
(a + bi)·(c + di) = ac - bd + (ad + bc)i
순서쌍으로 표현
(a, b)·(c, d) = (ac - bd, ad + bc)- 복소수의 곱셈 연산의 성질
- 결합법칙 : (a, b) · ((c, d) · (e, f)) = ((a, b) · (c, d)) · (e, f)
- 교환법칙 : (a, b) · (c, d) = (c, d) · (a, b)
- 분배법칙 : (a, b) · ((c, d) + (e, f)) = (a, b)·(c, d) + (a, b)·(e, f)
- 항등원 : (a, b) · (1, 0) = (a, b)
- 복소수의 크기와 기호 표기 방식
- 복소수의 크기는 2차원 벡터와 동일하게 실수부와 허수부의 각 요소를 제곱해 더한 다음, 제곱근을 취하는 방식으로 계산
- 복소수의 크기는 실수와 동일하게 절대값 기호를 써서 나타내며 복소수의 노름(Norm)이라고도 부른다.
|(a, b)| = |(a, -b)| = sqrt(a^2 + b^2)- 크기가 1인 복소수를 단위 복소수(Unit complex number)라고 부른다.
- 복소수의 곱셈 역원은 두 복소수의 관계를 나타내는 컬레(Conjugate) 복소수를 통해 나타낼 수 있다.
- 임의의 복소수를 c라고 하면 c의 컬레 복소수는 * 첨자 기호를 사용한 c^*로 표시한다.
- 임의의 복소수 a + bi의 켤레 복소수 c^*는 다음과 같이 정의한다.
c = a + bi = (a, b)
c^* = a - bi = (a, -b)- 켤레 복소수의 기호는 마치 연산처럼 사용할 수 있으며, 다음 성질이 성립된다.
(c^*)^* = c
c^*c = cc^*
(c_1c_2)^* = c_2^*c_1^*- 복소수 곱셈의 역원
임의의 복소수 c에 대한 곱셈의 역원을 c^-1라고 할때
그 역원의 분모와 분자에 각각 컬레 복소수를 곱하면
c^-1 = 1/c = c^* / (cc^*)
켤레 복소수의 성질에 따라 분모와 허수부가 제거되면서 역원의 표현이 가능
(a + bi)^-1 = 1 / (a + bi)
= (a - bi) / ((a + bi)(a - bi))
= (a - bi) / (a^2 + b^2)
복소수 c에 대한 곱셈의 역원 c^-1은 컬레 복소수와 복소수 크기에 관힌 식으로 나타낼 수 있음
c^-1 = c^* / |c|^2- 위 식에서 복소수 크기가 1인 단위 복소수라면 분모의 값은 1이 된다.
- 즉, 단위 복소수의 곱셈 역원은 바로 켤레 복소수가 된다.
복소평면
- 실수는 수직선이라는 1차원 직선을 사용해 시각적으로 표현한다.
- 복소수는 실수부와 허수부라는 두 개의 독립된 체계를 가졌다.
- 이를 시각적으로 나타내려면 직선보다는 확장된 체계를 사용해야 한다.
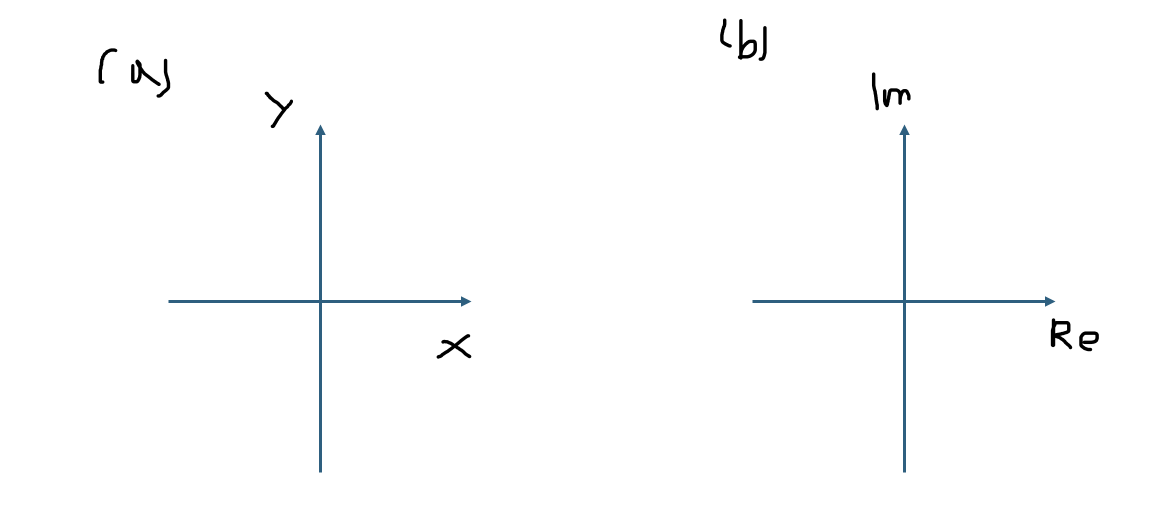
- 위 그림의 (a)와 같이 2차원 실벡터 공간 R^2의 벡터 (a, b)를 표현하기 위해 서로 직교하는 x축과 y축을 사용한 것 처럼, 복소수 역시 (b)와 같이 실수부에 해당하는 실수축과 허수부에 해당하는 허수축을 직각으로 교차시키는 방식으로 표현한다.
- 이를 복소평면(Complex plane)이라고 부른다.
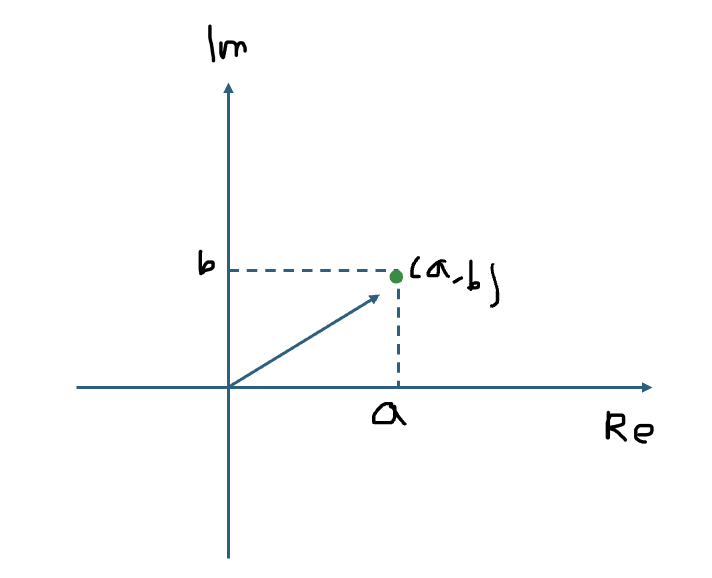
- 복소평면의 두 축의 이름을 순서대로 실수축(Re)와 허수축(Im)으로 실정하면 순서쌍으로 표현한 복소수 (a, b)는 위 그림과 같이 좌표처럼 평면 상에 표현할 수 있다.

- 크기가 1인 단위 복소수를 모아 복소평면에 표현하면 위 그림과 같이 단위원의 형태가 만들어진다.
단위 복소수와 곱
- 단위 복소수는 곱셈에 대해 특별한 성질을 만족한다.
- 허수부가 0인 임의의 복소수 (a, 0)에 대해 i라는 단위 복소수를 곱하면 다음과 같이 전개된다.
(a + 0i)·(0 + i) = (0 + ai) = (0, a)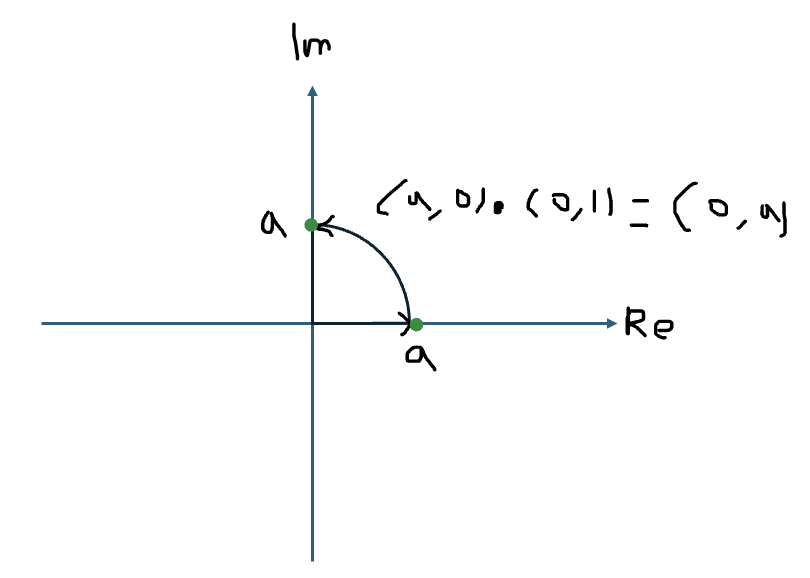
- 실수 a와 허수 i와의 곱셈 연산 결과 (0, a)를 복소평면 상에 나타내면 위 그림과 같이 복소수 (a, 0)을 90° 회전시킨 결과와 같다.
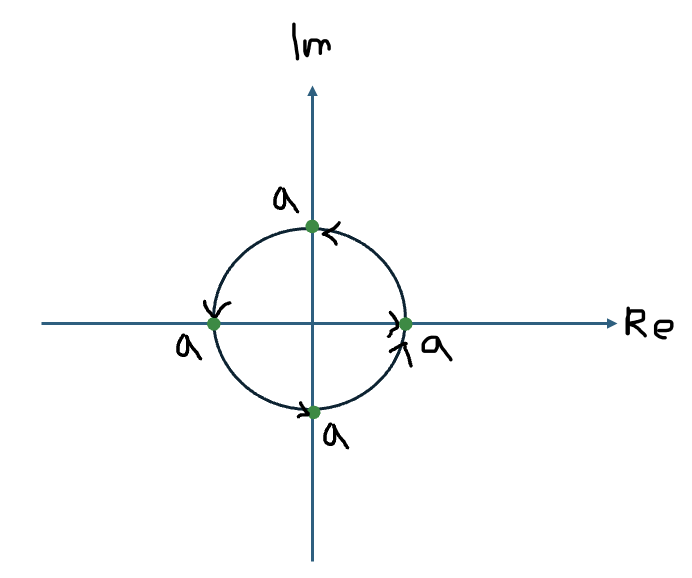
- 복소수 (0, a)에 복소수 i를 한번 더 곱해보면, (-a, 0)이 나온다.
- (-a, 0)에 또 i를 곱하면 (0, -a)가 나오고, (0, -a)에 i를 곱하면 (a, 0)이 되어 원래 값으로 돌아온다.
- 이를 정리하면 위 그림과 같다.
- 임의의 복소수에 단위 복소수 i를 곱한 결과는 해당 복소수를 90° 회전시킨 결과와 같음을 알 수 있다.
- 즉, 임의의 복소수 (a, b)에 복소수 i를 곱한 결과는 항상 실수부와 허수부의 값이 바뀌어 다음과 같은 식으로 표현된다.
(a, b) · (0, 1) = (-b, a)- 위 식은 좌표 평면에서의 90° 회전과 동일한 좌표값을 만들어낸다.
- 따라서 임의의 복소수에 복소수 i를 곱하면 항상 복소평면 상에서 90° 회전을 한다고 볼 수 있다.
- 삼각함수의 공식 cos^2Θ + sin^2Θ = 1을 이용해 단위원을 형성하는 임의의 단위 복소수 (a, b)를 다음과 같이 삼각함수로 표현할 수 있다.
(a, b) = cosΘ + isinΘ = (cosΘ, sinΘ)- 삼각함수로 나타낸 단위 복소수에 임의의 복소수 (x, y)를 곱하면 복소수 곱셈 식은 다음과 같이 전개된다.
(cosΘ, sinΘ)·(x, y) = (xcosΘ - ysinΘ, ycosΘ + xsinΘ)
위 식은 2차원 공간의 회전행렬 R에 2차원 벡터 (x, y)를 곱한 결과와 같다.
R = ┌ cosΘ -sinΘ ┐
└ sinΘ cosΘ ┘
┌ cosΘ -sinΘ ┐ ┌ x ┐ = ┌ xcosΘ - ysinΘ ┐
└ sinΘ cosΘ ┘ └ y ┘ └ xsinΘ + ycosΘ ┘- 위 식을 통해 임의의 복소수에 단위 복소수를 곱하는 것은 복소평면에서의 회전 변환을 의미하는 것을 알 수 있다.
- 서로 다른 각을 갖는 2개의 단위 복소수를 곱한 결과
(cosα, sinα) · (cosβ, sinβ) = (cosαcosβ - sinαsinβ, sinαcosβ + sinβcosα)
위 식은 삼각함수의 덧셈 정리에 의해 다음과 같이 간단하게 표기된다.
(cos(α + β), sin(α + β))- 위 식을 보면, 서로 다른 두 각을 회전 변환한 후 곱셈 연산을 하는 것은 두 각의 합을 회전 변환하는 것과 동일한 것을 알 수 있다.
- 복소수 곱셈의 항등원 (1, 0)의 의미
- 복소수 곱셈의 항등원은 실수에서의 곱셈의 항등원과 동일하게 1이다.
- 복소수 1역시 단위 복소수로서, 이를 삼각함수로 표현하면 0°에 대응하는 수다.
- 따라서 곱셈의 항등원을 곱한다는 의미는 아무런 변화가 일어나지 않는 0°의 회전 변환이라 해석할 수 있다.
- 실수에서 크기가 1인 수는 오직 1과 -1 두가지만 존재한다.
- 1과 -1을 복소수에서 바라보면 (1, 0), (-1, 0)에 대응되고, 이들과의 곱은 각각 0°와 180°의 회전 변환으로 해석할 수 있다.
(1, 0) = (cos0°, sin0°)켤레 복소수의 회전 변환
- 켤레 복소수를 복소 평면에 나타내면 아래 그림과 같다.
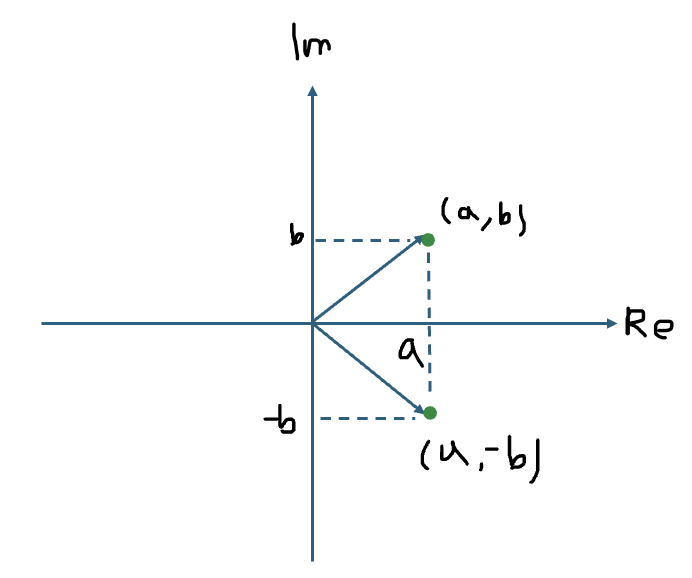
- 임의의 복소수 (a, b)의 켤레 복소수는 (a, -b)이다.
- 임의의 복소수와 그 켤레 복소수는 실수부 축(Re)을 중심으로 서로 대칭된 형태를 이룬다.
- 단위 복소수를 (cosΘ, sinΘ)로 표현하면 이의 켤레 복소수는 (cosΘ, -sinΘ)가 된다.
- 이때 삼각함수의 성질을 활용하면 다음과 같이 켤레 복소수를 표현할 수 있다.
(cosΘ, -sinΘ) = (cos(-Θ), sin(-Θ))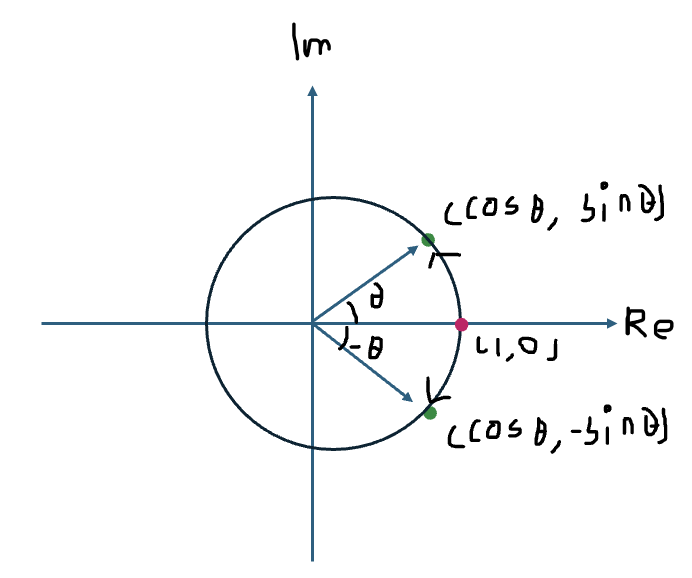
- 단위 복소수가 위 그림과 같이 실수 축에 위치한 단위 복소수 (1, 0)을 각 Θ만큼 회전한 수를 의미하면, 켤레 복소수는 반대 방향인 -Θ만큼 회전한 수를 의미한다.
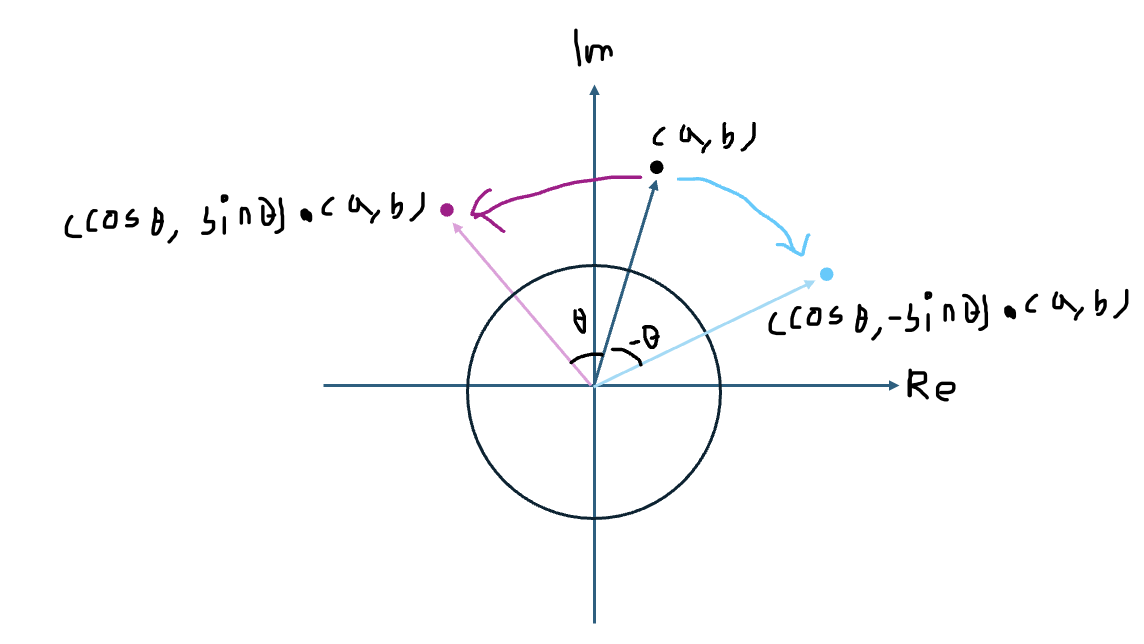
- 임의의 복소수 (a, b)에 단위 복소수를 곱하면 위 그림과 같이 보라색의 궤적을 따라 반시계 방향의 회전이 발생하는데 반해, 단위 복소수의 켤레 복소수를 곱하면 하늘색의 궤적을 따라 시계 방향의 회전이 발생한다.
- 단위 복소수와 그 켤레 복소수를 곱한 값은 복소수의 크기의 제곱이므로 1이 된다.
c·c^* = a^2 + b^2 = sin^2Θ + cos^2Θ = 1- 이 식을 변환의 관점에서 해석하면 각 Θ만큼 회전한 후에 바로 -Θ만큼 거꾸로 회전하는 변환을 의미한다.
- 이 결과는 아무런 회전도 일어나지 않는 0° 회전 변환을 의미하므로 복소수 곱셈의 항등원 (1, 0)이 된다.
복소수와 행렬의 관계
- 복소수를 수의 관점이 아닌 변환의 관점에서 바라본다면 2차원 복소평면 상의 복소수는 2차원 행렬에 대응할 수 있다.
- 회전을 수행하는 단위 복소수와 2차원의 회전 변환행렬이 동일하다고 가정하고 수식을 전개하면 다음과 같다.
cosΘ + isinΘ = ┌ cosΘ -sinΘ ┐
└ sinΘ cosΘ ┘- 회전 변환행렬을 cosΘ와 sinΘ에 대해 분리해 정의하면 다음과 같다.
cosΘ + isinΘ = cosΘ·┌ 1 0 ┐ + sinΘ·┌ 0 -1 ┐
└ 0 1 ┘ └ 1 0 ┘- 실수부에 대응하는 행렬을 I로, 허수 i에 대응하는 행렬을 J로 정의
I = ┌ 1 0 ┐
└ 0 1 ┘
J = ┌ 0 -1 ┐
└ 1 0 ┘- 실수부에 대응하는 행렬 I는 어떤 수에 곱했을 때 아무 변화가 없는 항등행렬이다.
- 이는 곱셈의 항등원 I와 동등한 개념이다.
- 한편 허수 i에 대응하는 행렬 J는 90° 회전 변환행렬인데 이를 두번 곱하면 -I가 나오며, 이는 -I에 대응한다고 볼 수 있다.
J·J = ┌ -1 0 ┐ = -I
└ 0 -1 ┘
이는 두 번 곱하면 -I가 나오는 허수 단위의 성질과도 일치함
i·i = -1
출처
https://m.yes24.com/Goods/Detail/107025224
이득우의 게임 수학 - 예스24
39가지 실시간 렌더링 게임 프로그래밍 실습 예제를 하나씩 따라 해보며 독자가 직접 체득하는 흥미로운 게임 수학의 세계! 게임 개발자와 그래픽 아티스트들이 궁금해 했던 3D 가상 세계와 메타
m.yes24.com
'게임수학' 카테고리의 다른 글
| [게임수학] 사원수(Quaternion) (0) | 2024.05.06 |
|---|---|
| [게임수학] 극한과 오일러 공식 (1) | 2024.05.03 |
| [게임수학] 모델링과 뷰 (0) | 2024.04.28 |
| [게임수학] 절두체(Frustum) (1) | 2024.04.25 |
| [게임수학] 원근 투영과 깊이 (1) | 2024.04.23 |
