트렌스폼
- 게임은 주로 게임 엔진에 의해 개발된다.
- 게임 엔진의 편리한 인터페이스로 개발자들은 손쉽게 콘텐츠를 제작할 수 있다.
- 게임 엔진의 기저에 가상 세계를 만드는 수학과 게임 콘텐츠를 구성하는 데이터를 효과적으로 관리하는 기술이 지탱되고 있음
- 게임 엔진은 씬(Scene)과 리소스(Resource)라고 불리는 공간과 데이터를 결합해 최종 화면을 렌더링되도록 설계되었다.
- 씬을 구성하는 게임 오브젝트는 게임 공간에 항상 존재해야 하기 때문에 언제나 공간 내 배치 정보를 가져야한다.
- 게임 엔진은 게임 오브젝트의 배치 정보를 위치, 회전, 크기로 구성된 트랜스폼(Transform)의 정보를 사용해 관리함
- 게임 개발자는 게임 오브젝트의 트랜스폼을 구성하는 위치, 회전, 크기에 대한 정보를 입력해 게임 공간에 게임 오브젝트를 배치함
- 최종 렌더링 과정에서는 트랜스폼 정보로부터 모델링 행렬이라 불리는 행렬을 사용해 렌더링할 물체의 정점을 변환한다.
모델링 행렬
- 트렌스폼은 크기, 회전, 이동의 세 가지 데이터로 구성되며, 각각은 다음과 같다.
- 크기(S) : 2차원 벡터 (s1, s2)
- 회전(R) : 각 Θ
- 이동(T) : 2차원 벡터 (t1, t2)
- 각 데이터는 크기, 회전, 이동에 대한 세 가지 어파인 변환행렬에 대응된다.
┌ sx 0 0 ┐
S = | 0 sy 0 |
└ 0 0 1 ┘
┌ cosθ -sinθ 0 ┐
R = | sinθ cosθ 0 |
└ 0 0 1 ┘
┌ 1 0 tx ┐
T = | 0 0 ty |
└ 0 0 1 ┘- 행렬 곱의 성질을 활용하면 3가지 어파인 변환을 모두 수행하는 하나의 행렬을 만들어 낼 수 있다.
- 행렬 곱은 교환 법칙이 성립하지 않기 때문에, 어파인 변환을 적용하는 순서를 결정하고 행렬 곱을 진행해야 함
- 크기, 회전, 이동 3가지 어파인 변환을 순서대로 적용하는 경우의 수는 다음과 같이 6가지가 존재한다.
- S·R·T
- S·T·R
- T·S·R
- T·R·S
- R·T·S
- R·S·T
- 변환 순서는 오른쪽에서 왼쪽으로 진행된다.
- 열 기준 행렬을 사용하기 때문
- 6가지 경우 중 어떤 변환 순서를 선택해야 하는가?
- 이동의 경우 게임 오브젝트의 트랜스폼의 이동 값을 (tx, ty)를 설정했을 때, 게임 오브젝트가 배치되어야 할 위치는 개발자가 설정한 이동 값이 되어야 한다.
- 6가지 어파인 변환에서 개발자가 입력한 이동 값과 게임 오브젝트가 배치된 좌표가 서로 다른 변환이 존재

- 물체 트랜스폼에 45도 회전과 (0, 1) 이동을 순서대로 설정한다고 가정
- 이 경우 물체의 최종 위치는 (0, 1)이 되어야 함
- (b)와 같이 (0, 1) 이동 변환을 하고 45도 회전 변환을 적용하면 물체의 위치는 다른 좌표로 바뀐다.
- 회전 변환 대신 크기 변환을 사용해도 마찬가지
- 이동 변환을 통해 원하는 위치로 물체를 이동시키려면 이동 변환은 가장 마지막에 진행해야 한다.
- 6가지에서 3번 T·S·R과 4번 T·R·S 2가지로 압축된다.
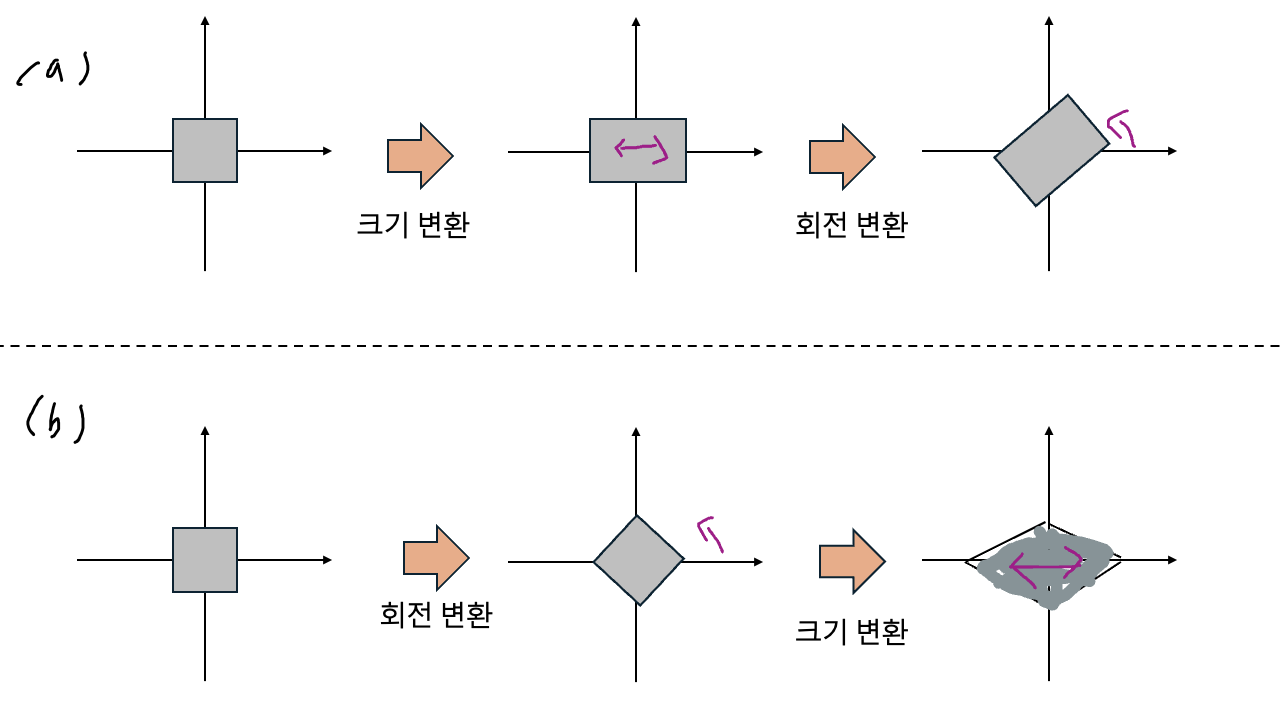
- 크기 변환과 회전 변환 두 가지 중 어떤 변환을 먼저 해야하는가?
- 정사각형 물체에 크기 변환 값을 (2, 1)로 설정해 좌우로 길게 늘리면 직사각형 형태가 된다.
- 크기 변환을 먼저 적용한 (a)의 최종 결과는 직사각형이 회전한 모습
- 회전 변환을 먼저 적용한 (b)의 경우 마름모가 되는 것을 볼 수 있다.
- 회전 변환은 물체의 형태를 그대로 보존해주는 강체 변환이다.
- 크기 변환을 먼저 적용해 물체의 형태를 확정한 후 강체 변환인 회전 변환을 적용해 형태를 유지하는 것이 가장 직관적인 변환을 수행한다고 할 수 있다.
- 보편적으로 사용하는 트랜스폼의 변환은 크기 -> 회전 -> 위치 순서로 이루어진다.
T·R·S- 행렬 곱을 사용해 3가지 변환을 수행하는 합성 행렬을 생성할 수 있다.
- 트랜스폼의 정보로 만들어지는 모델링 행렬(Modeling matrix) M은 다음과 같다.
┌ cosΘ·sx -sinΘ·sy tx ┐
M = T·R·S = | sinΘ·sx cosΘ·sy ty |
└ 0 0 1 ┘로컬 공간과 로컬 축
- 하나의 물체를 표현하기 위해 만들어진 메시 데이터는 자신만의 공간에서 물체를 구성하는 각 정점의 위치 정보가 저장된다.
- 물체의 정보를 담기 위해 부여한 공간을 로컬 공간(Local space)이라고 한다.
- 게임 콘텐츠는 단일 물체가 아닌 다양한 종류의 물체가 모여 배경을 이루므로, 여러 물체를 모아 담을 수 있는 별도의 공간이 있어야한다.
- 여러 물체를 모아 게임 콘텐츠를 만드는데 사용되는 새로운 공간을 월드 공간(World space)이라고 한다.
- 게임 콘텐츠에는 게임 오브젝트마다 월드 공간과 로컬 공간이라는 두 공간 개념이 존재한다.
- 게임 제작 과정에서는 주어는 두 개의 공간 정보를 적절하게 활용해야 한다.
- 비행기 게임을 만들기 위해선 기본적으로 월드 공간을 중심으로 설정된 비행기의 위치 좌표가 필요하다.
- 앞으로 나아가는 비행기의 방향을 조종하라면 월드 공간과 무관하게 비행기가 바라보는 방향 정보도 필요하다.
- 물체를 기준으로 설정된 방향 정보를 로컬 축(Local axis)이라고 한다.
- 로컬 축 정보는 로컬 공간의 기저벡터와 동일한 값을 가진다.
- 게임 엔진은 개발의 편의성을 위해 트렌스폼에서 로컬 축 데이터도 함께 제공한다.
- 각 로컬 축은 월드의 X, Y, Z축과 구분하기 위해 다음과 같은 이름으로 부른다.
- 로컬 축 +X : 라이트벡터(Right Vector)
- 로컬 축 +Y : 업벡터(Up Vector)
- 로컬 축 +Z : 포워드벡터(Forward Vector)
- 트렌스폼의 이동과 크기 정보가 변경되더라도 게임 오브젝트가 보는 방향은 변함이 없기 때문에, 로컬 축 정보는 오직 회전 정보에만 영향을 받는다.
- 2차원 평면에서 게임 오브젝트의 트렌스폼에 새로운 회전 값이 설정되면, 로컬 축을 구성하던 표준기저벡터들은 이에 따라 변한다.
- 로컬 공간의 표준기저벡터 e1이 변화된 값을 r로, e2가 변화된 값을 u로 표현하면 트렌스폼에서 각 Θ로 설정한 로컬 축의 값은 다음과 같다.
r = (cosΘ, sinΘ)
u = (-sinΘ, cosΘ)- 로컬축 벡터의 원소를 각각 r = (rx, ry)와 u = (ux, uy)로 지정하면 어파인 회전 변환행렬은 삼각함수대신 다음과 같은 로컬 축 벡터를 사용해 생성할 수 있다.
┌ rx ux 0 ┐
R = | ry uy 0 |
└ 0 0 1 ┘- 모델링 행렬 M 역시 삼각함수대신 로컬 축 정보를 사용해 계산할 수 있다.
┌ rx·sx ux·sy tx ┐
R = | ry·sx uy·sy ty |
└ 0 0 1 ┘리소스 관리
- 게임 오브젝트에 트랜스폼을 설정하는 작업은 모델링 행렬을 사용해 각 게임 오브젝트에 부여된 로컬 공간 정보를 월드 공간 정보로 변환하는 것이다.
- 씬에서 게임 오브젝트들은 각자 트랜스폼 정보를 포함하고 있었다.
- 동일한 방법으로 게임 오브젝트마다 리소스 정보를 포함한다고 하면, 다수의 게임 오브젝트가 동일한 메시를 사용할 경우 게임 오브젝트마다 용량이 큰 메시 정보를 포함하게 되어 메모리 공간이 낭비될 것이다.
- 리소스 데이터는 여러 게임 오브젝트들이 함께 사용할 수 있는 공유 자원의 형태로 관리되는 것이 바람직함
- 게임 엔진은 씬과 무관하게 리소스를 모아두는 저장소를 별도로 제공한다.
- 이를 리소스 저장소(Resource repository)라고 부른다.

- 게임 엔진은 리소스 저장소를 효율적으로 관리하기 위해 위 그림과 같이 리소스를 유형별로 나누고 각 리소스에 고유한 키를 부여한다.
- 게임 오브젝트에는 리소스 데이터를 가리키는 리소스 키 값만 저장하도록 설계한다.
- 그렇다면 메모리 공간의 소비를 줄일 수 있을 것
게임 엔진의 워크플로우
- 게임 엔진은 씬과 리소스를 관리하는 기반을 제공하면서 게임 콘텐츠가 효율적으로 구동되기 위해 실행 과정에 대해서도 고도화된 표준 들도 함께 제시하고 있다.
- 게임 엔진이 제공하는 실행의 흐름을 워크플로우(Workflow)라고 한다.

- 게임 엔진의 워크플로우는 씬을 완성하는 과정과 완성된 씬으로부터 화면을 그려내는 과정으로 구성된다.
- 리소스 로딩 단계
- 게임에서 사용하는 리소스를 불러들이는 과정
- 화면을 구성할 때 사용하는 메시, 텍스처와 같은 리소스는 게임을 진행하면서 불러들이기에는 데이터 양이 크기 때문에 게임을 시작하기 전에 미리 불러들여 메모리에 올려둬야 안정적으로 게임을 진행할 수 있다.
- 해당 작업은 게임이 시작되기 전에 한번만 실행된다.
- 씬 구축 단계
- 게임 콘텐츠를 구성하는 씬을 설계하는 과정
- 씬에 속한 게임 오브젝트가 생성되고, 생성된 게임 오브젝트의 트랜스폼 정보가 설정된다.
- 1단계에서 생성된 리소스 정보가 게임 오브젝트에 연결된다.
- 게임 로직 단계
- 프레임마다 게임 오브젝트에 포함되어 있는 트랜스폼 값을 변경하는 과정
- 렌더링 로직 단계
- 3단계에서 완성된 씬 정보를 바탕으로 최종 화면을 만들어내는 과정
- 게임 오브젝트에 설정된 트랜스폼 정보를 중심으로 게임 오브젝트에 연결된 메시와 텍스처의 리소스 데이터를 활용해 최종 화면을 그려낸다.
- 리소스 로딩 단계
렌더링 파이프라인
- 게임 제작에서 렌더링은 그릴 물체의 정보를 하드웨어인 GPU에 넘겨 GPU가 처리하도록 위임하는 것이 일반적이다.
- GPU에 그릴 물체의 정보를 전달하면 GPU는 하드웨어에 설정된 워크플로우를 통해 렌더링을 진행하고 그 결과를 화면에 띄운다.
- GPU 내부에 설정된 워크플로우를 렌더링 파이프라인(Rendering pipeline)이라고 부른다.

- 렌더링 파이프 라인을 단순화시키면 다음과 같다.
- 정점 변환 단계
- 게임 오브젝트에 연결된 메시가 가지고 있는 모든 정점의 정보를 변환하는 과정
- 메시에 설정된 정점의 데이터는 로컬 공간을 기준으로 설정되어 있지만, 다양한 게임 오브젝트들이 월드 공간을 중심으로 그려지기 위해서는 정점의 최종 위치가 월드 공간을 중심으로 지정되어야 한다.
- 정점 처리 단계
- 화면에 그려질 정점의 최종 위치 값을 구하는 과정
- 모델링 행렬에 로컬 공간의 좌표를 곱하면 월드 공간을 기준으로 좌표가 변환된다.
- 픽셀화 단계
- 메시를 구성하는 삼각형마다 픽셀화를 진행하는 과정
- 무게중심좌표를 활용해 각 삼각형 영역에 속하는 픽셀들을 추려내고 이들의 색상을 결정한다.
- 픽셀 처리 단계
- 삼각형을 구성하는 각 픽셀의 최종 색상을 구하는 과정
- 텍스처로부터 해당 픽셀의 UV에 대응되는 색상을 가져온 후에 필요하다면 추가로 조명 효과 등을 적용해 최종 픽셀의 색상을 설정한다.
- 정점 변환 단계
- 정점 변환 시 게임 오브젝트를 렌더링하려면 메시 정보와 모델링 행렬이 필요하다.
- 원본 메시에 모델링 행렬을 곱하면 메시 정보를 공유하는 다른 게임 오브젝트에 영향을 미친다.
- 정점 변환 과정에서 사용되는 메시 데이터는 원본 데이터를 복제해 사용해야 한다.
- 렌더링 파이프라인을 시작하는 함수가 호출되는 상황을 드로콜(Drawcall)이 발생된다고 표현함
- GPU는 렌더링 파이프라인을 구성하는 대부분 과정을 고정시키고 이에 특화된 하드웨어 칩을 사용해 계산한다.
- 몇몇 중요한 과정은 개발자들이 설계한 로직을 실행하도록 함수를 제공
- 이를 셰이더(Shader)라고 부른다.
- GPU에서도 정점 처리 단계에서는 개발자들이 변환을 직접 설계하도록 정점 셰이더(Vertex Shader) 함수를 제공
- 정점 셰이더 함수를 통해 모든 정점의 변환이 완료되면, 메시를 구성하는 삼각형을 하나씩 화면에 그려야 한다.
- 메시의 인덱스 버퍼로부터 가져온 삼각형 영역은 3단계 픽셀화 과정을 통해 화면에 그려진다.
- GPU에서는 삼각형을 구성하는 픽셀을 파편(Fragment)라고도 부른다.
- 개발자들이 직접 최종 픽셀의 색상을 계산할 수 있도록 파면 셰이더(Fragment Shader) 또는 픽셀 셰이더(Pixel Shader) 함수를 제공한다.
뷰
- 게임 콘텐츠의 무대가 되는 월드 공간은 굉장히 넓은 영역이다.
- 카메라는 자신이 출력할 화면의 해상도를 가지고 월드의 일부를 그려낸다.
- 카메라가 출력할 화면의 크기 정보를 뷰포트(Viewport)라고 부른다.
- 사용자가 보는 게임 공간의 크기가 뷰포트다.
- 카메라에 설정된 뷰포트 정보를 바탕으로 월드 공간의 일부분을 렌더링해야 한다.
- 이를 위해 카메라를 중심으로 물체의 트랜스폼을 재조정하는 작업이 필요하다.
- 카메라 중심으로 변환한 공간을 뷰 공간(View space)이라고 한다.
- 로컬 공간, 월드 공간, 뷰 공간의 개념을 정리하면 다음 그림과 같다.

- 어떤 게임 오브젝트가 (10, 10)에 위치하고 카메라는 월드 공간 (-10, -10)에 위치한 경우
- 카메라의 위치를 원점으로 삼았다면 카메라로부터 해당 게임 오브젝트의 상대적인 위치는 다음 그림과 같이 (20, 20)이 된다.

- 월드 공간의 좌표를 뷰 공간의 좌표로 변환시키는 방법
- 모델링 행렬은 로컬 공간의 좌표를 월드 공간의 좌표로 변환해주는 행렬이다.
- 이와 동일하게 월드 좌표를 카메라 중심의 좌표로 변환하는 행렬이 있다.
- 이를 뷰 행렬 V 라고 한다.
- 월드의 원점과 카메라의 관계만 생각했을 때 카메라 중심에서 월드 원점의 상대 좌표는 (10, 10)이 된다.
- 이는 월드 공간에 설정된 모든 게임 오브젝트의 위치 좌표에 상대 좌표 (10, 10)을 더해주면 뷰 공간의 좌표를 얻을 수 있음을 의미
- 따라서 게임 오브젝트의 월드 공간 좌표 (10, 10)에 카메라의 위치와 월드 원점과의 상대적 거리 (10, 10)을 더하면 최종 좌표 (20, 20)을 얻게 된다.
- 카메라의 위치를 기준으로 측정한 월드 원점의 상대 좌표 (10, 10)은 월드 공간에서 측정된 카메라 위치 (-10, -10)을 반전시켜 알 수 있다.
- 이는 이동 행렬의 역행렬을 사용해 계산
- 따라서 카메라에 트랜스폼이 설정된 경우, 여기서 이동 행렬의 역행렬을 계산하면 뷰 행렬이 완성된다.
┌ 1 0 -tx ┐
V = | 0 0 -ty |
└ 0 0 1 ┘- 뷰 행렬이 완성되면 로컬 공간의 좌표 v_local)을 뷰 공간의 좌표 v_view로 변환하는 행렬을 설계해야한다.
- 뷰 행렬 V와 모델링 행렬 M을 곱한 행렬 VM은 로컬 공간의 뷰 공간으로 변환하는 기능을 수행한다.
- 행렬 VM을 메시 정점에 곱하면 모든 정점의 위치는 카메라를 중심으로 재배치 된다.
v_view = V · M · v_local
출처
https://m.yes24.com/Goods/Detail/107025224
이득우의 게임 수학 - 예스24
39가지 실시간 렌더링 게임 프로그래밍 실습 예제를 하나씩 따라 해보며 독자가 직접 체득하는 흥미로운 게임 수학의 세계! 게임 개발자와 그래픽 아티스트들이 궁금해 했던 3D 가상 세계와 메타
m.yes24.com
'게임수학' 카테고리의 다른 글
| [게임수학] 극한과 오일러 공식 (1) | 2024.05.03 |
|---|---|
| [게임수학] 복소수 (1) | 2024.05.03 |
| [게임수학] 절두체(Frustum) (1) | 2024.04.25 |
| [게임수학] 원근 투영과 깊이 (1) | 2024.04.23 |
| [게임수학] 벡터의 외적 (0) | 2024.04.23 |
