자연 지수 함수
- 무리수 e와 허수 단위 i, 그리고 삼각함수와의 관계를 이용해 나타낸 오일러 공식은 다음과 같다.
//오일러 공식
e^iθ = cosθ + isinθ- 오일러 공식을 이해하려면 좌변의 자연지수함수 f(x) = e^x와 우변에 있는 두 삼각함수 sin 함수와 cos 함수의 미분을 이해하고, 이들을 급수로 표현하는 방식을 알아야 한다.
무리수 e

- 스위스 수학자 야코프 베르누이(Jakob Bernouli)는 아래 수식으로 복리 수익을 연구하고 있었다.
y = (1 + 1/x)^x- 굉장히 큰 값을 에 대입할 수록 결괏값이 특정 상수 2.7182818…에 근접한다는 사실을 알아냈다.
- 이 수를 무리수 라고 부른다.
- 무리수 를 극한(Limit)과 무한대(∞)의 개념을 사용해서 다음과 같이 표현할 수 있다.
e = lim(1 + 1/x)^x
x->∞- ∞로 표시하는 무한대(Infinity)란 특정한 수를 가리키는 것이 아니다.
- 어떤 실수보다도 큰 상태를 의미한다.
- 극한이란 어떤 값 x가 지정한 값 a에 한없이 가까워질 때 함수 f(x)가 한없이 가까워지는 값 L을 의미한다.
- 수렴(Converge)
- 극한의 결괏값이 특정 값에 한없이 가까워지면 이를 어떤 값에 수렴한다고 표현
- 발산(Diverge)
- 극한의 결괏값이 무한대로 증가하거나 여러 값을들 오고가면 발산한다고 표현
자연 지수 함수
- 거듭제곱(Exponentiation)
- 같은 수를 여러번 곱하는 작업
3^5 = 3⋅3⋅3⋅3⋅3- 지수(Exponent)
- 곱하는 횟수
- 위 예시에서의 5
- 밑(Base)
- 곱하는 수
- 위 예시에서의 3
- 지수법칙(Law of exponents)
1. 밑이 같은 거급제곱 간의 곱셈은 지수를 더한 거듭제곱과 동일함
a^m ⋅ a^n = a^m+n
2. 거듭제곱의 거듭제곱은 지수를 곱한 거듭제곱과 동일함
(a^m)^n = a^m⋅n
거듭 제곱의 개념은 수를 세는 자연수에서 비롯됐지만, 자연수가 아닌 0으로도 확장 가능
곱셈의 항등원 1을 활용해 0의 거듭제곱의 값은 다음과 같이 유도할 수 있다.
a^m = a^(m+0) = a^m ⋅ a^0 = a^m ⋅ 1
3. 지수가 0인 거듭제곱은 항상 1의 값을 갖는다.
a^0 = 1- 지수함수(Exponential function)
- 지수 법칙에 따라 지수함수의 가 0이면, 출력은 항상 이다. 따라서 이 함수는 늘 좌표 (0,1)을 지난다.
f(x) = a^x- 자연무리함수
- 밑이 무리수 인 지수함수이다.
- 언제나 (0,1)을 지나며, 아래 그래프와 같이 가 커질 수록 급격히 증가하는 형태
f(x) = e^x
미분
- 미분 가능한 함수를 대상으로, 특정 지점에서의 접선의 기울기를 측정하는 작업
- 자연지수함수, 함수, 함수 모두 미분 가능한 함수

- 할선(Secant line)
- 곡선과 직선이 두 점에서 만날 때의 직선.
- 어떤 미분 가능한 함수가 주어졌을 때, 가 일 때와 일 때 대응 되는 두 좌표를 연결하면 할선이 생김
- 할선의 기울기는 다음과 같이 구할 수 있다
m = (f(b)−f(a)) / (b−a)- a는 고정하고 b를 a쪽으로 서서히 이동시켜 b가 a에 한없이 가까워지는 경우 a지점의 기울기처럼 보임

- 접선(Tangent Line)
- 곡선과 직선이 한 점에서 만날 때의 직선.
- 한없이 가까워지는 개념을 사용해서 특정 지점에서의 기울기를 나타내는 접선을 만들 수 있다.
- 극한의 개념을 사용해서 기울기 을 구하면 다음과 같다
m = lim (f(b) - f(a)) / (b - a)
b->a- 여기서 는 에다가 한없이 작은 값인 를 더한 것과 같다. 따라서 아래와 같이 바꿔볼 수 있다.
m = lim (f(a+h) - f(a)) / h
h->0- 미분 계수(Differential coefficient)
- 주어진 값에 대한 접선의 기울기이다.
- 위 식은 에서의 미분 계수라고 볼 수 있다.
도함수
f'(x) = lim f(x+h) - (f) / h
h->0- 임의의 수 에 대한 미분 계수를 구할 수 있도록 일반화한 함수
- 보통 미분이라고 부르며 f'로 표현
- 이 식을 가지고, 자연지수함수, 함수, 함수에 대한 도함수(Derviative)를 계산할 수 있다.

- 상수함수
- f(x) = c
- 정의역과 무관하게 항상 일정한 값을 가지는 함수
- 도함수 계산식에 대입하면, 그 결과값은 언제나 이 된다.
- 이것은 상수함수의 모든 에 대한 접선의 기울기가 이라는 것을 뜻한다.
- 극한의 여섯 가지 성질
(1) 두 함수 합의 극한값 = 각 극한값의 합
lim [f(x) + g(x)] = lim f(x) + lim g(x)
a→b x->a x->a
(2) 상수와 함수 곱의 극한값 = 함수 극한값과 상수의 곱
lim c⋅f(x) = c⋅lim f(x)
x->a. x->a
(3) 두 함수 곱의 극한값 = 각 극한값의 곱
lim [f(x)⋅g(x)] = lim f(x)⋅lim g(x)
x->a. x->a. x->a
(4) 두 함수 나눗셈의 극한값 = 각 극한값의 나눗셈
단, 분모의 극한값은 0이 아니여야 함
lim f(x)/g(x) = lim f(x) / lim g(x)
x->a x->a x->a
(5) 함수를 거듭제곱한 극한값 = 극한값을 거듭제곱한 값
lim [f(x)]^n = [lim f(x)]^n
x->a x->a
(6) 조임 정리(Squeeze theorem)
세 함수의 대소관계에서 양 끝의 극한값이 같다면, 가운데 극한값도 같다.
g(x) <= f(x) <= h(x) 에서
lim g(x) = lim h(x) = L 이면 lim f(x) = L 이 성립한다.
x->a x->a x->a- 거듭제곱 함수 f(x)= x^n의 도함수를 구하면
- f'(x)=n ⋅
f'(x) = e^x = f(x)무리수 e의 극한식으로부터 다음 수식을 유도해 볼 수 있음
lim (e^h - 1) / lim h = 1
h->0 h->0
무리수 e의 극한식은 다음과 같다.
e = lim(1 + 1/x)^x
x->∞
위 식에서 한없이 커지는 x를 1/h로 바꾸면 1/h는 0으로 수렴할 것
e = lim (1 + h)^(1/h)
h->0
위 식의 좌변에 극한을 취한다.
e는 h와 관련없는 상수이므로 극한을 대입해도 결과는 동일
lim e = lim (1 + h)^(1/h)
h->0 h->0
극한의 성질 5를 사용해 양변에 h승을 적용
lim e^h = lim 1 + lim h
h->0 h->0 h->0
분리된 상수함수항을 좌변으로 옮긴다.
lim (e^h - 1) = lim h
h->0 h->0- 유도해본 식을 활용해 자연지수함수의 도함수를 구할 수 있다.
도함수를 구하는 식은 다음과 같다.
f'(x) = lim f(x+h) - (f) / h
h->0
위 식에 자연지수함수 f(x) = e^x를 대입해 전개
f'(x) = lim e^(x+h) - e^x / h
h->0
= lim e^x·e^h - e^x / h // 지수 법칙을 사용해 분리
h->0
= lim e^x·(e^h - 1) / h // e^x로 묶어줌
h->0
= e^x·lim (e^h - 1) / h // h와 관련없는 e^x는 상수 취급 가능
h->0
= e^x lim (e^h - 1) / lim h // 극한의 성질 4를 사용해 분모와 분자를 각각 극한 값으로 분리
h->0 h->0
= e^x- 함수를 미분했을 때 그 결과가 원함수와 동일하다면 그 함수는 몇 번 미분하더라도 그 결과는 언제나 원함수와 동일하게 유지될 것
- 자연지수함수는 무한번 미분 가능하다는 성질을 가진다.
sin 함수와 cos 함수의 도함수
lim sin h / h = 1
h->0원의 넓이를 구하는 공식
Area(C) = π · r^2
원을 구성하는 각은 2π
1(rad)에 해당하는 부채꼴의 넓이는 π·r^2에서 22π를 나눈 1/2·r^2이 된다.
부채꼴의 넓이는 각의 크기에 비례해 커진다.
Area(CS) = Θ/2·r^2
Area(CS_1) = Θ/2
Area(T) = sinΘ / 2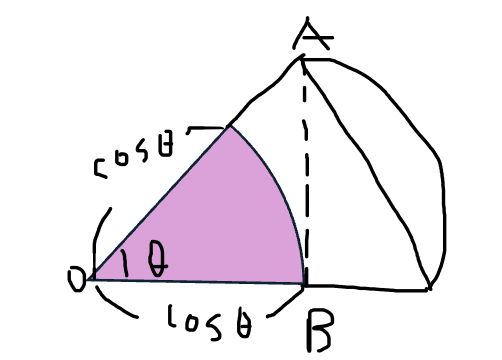
- 위 그림과 같이 선분 OB를 반지름으로 하는 작은 부채꼴 CS_2를 만들어보면, 작은 부채꼴 CS_2의 영역은 언제나 삼각형 내부에 속하게 된다.
- 선분 OB의 길이는 cosΘ이고, 이를 반지름으로 하는 부채꼴 CS_2의 넓이는 다음과 같다.
Area(CS_2) = Θ/2 · cos^2Θ- 부채꼴에 관련된 세 영역의 넓이 Area(CS_1), Area(T), Area(CS_2)를 구하는 공식을 통해 다음 대소 관계가 성립하는 것을 알 수 있다.
Θ/2·cos^2Θ <= sinΘ / 2 <= Θ/2
넓이 Area(CS_1)의 역수 2/Θ를 곱해 부등식을 정리
cos^2Θ <= sinΘ / Θ <= 1- 위 부등식의 Θ를 h로 변경한 후 우변의 극한값과 좌변의 극한값을 구하면 다음과 같다.
lim cos^2h <= lim sinh / h <= lim 1
h->0. h->0. h->0
우변의 극한 값은 상수이므로 1이다.
cos 함수는 각이 0도에 수렴할수록 그 값은 1에 수렴한다.
따라서 이를 제곱한 극한값 역시 1에 수렴한다.
극한의 성질 6으로 정리한 극한의 조임정리에 의해 좌우의 극한 값이 동일한 경우
가운데 위치한 sinh / h의 극한값 또한 1이된다.
따라서 lim sin h / h = 1 의 식이 성립함을 알 수 있다.
h->0- 추가로 알아두면 좋은 암수의 극한 값
lim cosh - 1 / h = 0
h->0
위 식은 다음 과정을 거쳐 유도된다.
lim cosh - 1 / h = lim (cosh - 1)·(cosh + 1) / (h·(cosh + 1))
h->0 h->0
= lim (cosh^2 - 1) / (h·(cosh + 1))
h->0
= lim -sin^2h / (h·(cosh + 1))
h->0
= lim sinh · lim -sin2h / h · lim 1/(cosh + 1)
h->0 h->0 h->0
= 0- 위에서 유도해본 식을 사용해 삼각함수의 도함수를 구해보기
f(x) = sinx의 도함수
f'(x) = lim (sin(x+h) - sinx) / h
h->0
= lim (cosh·sinx + cosx·sinh - sinx) / h
h->0
= sinx · lim (cosh - 1) / h + cosx · lim sinh / h
h->0 h->0
= cosx
f(x) = cosx의 도함수
f'(x) = lim (cos(x+h) - cosx) / h
h->0
= lim (cosx·cosh - sinx·sinh - cosx) / h
h->0
= cosx · lim (cosh - 1) / h - sinx · lim sinh / h
h->0 h->0
= -sinx- 두 삼각함수를 여러 번 미분할 경우
f(x) = sinx
f'(x) = cosx
f''(x) = -sinx
f'''(x) = -cosx
f''''(x) = sinx
f(x) = cosx
f'(x) = -sinx
f''(x) = -cosx
f'''(x) = sinx
f''''(x) = cosx- sin함수와 cos함수는 네 번 미분하면 원함수로 돌아오기 때문에 자연지수함수와 동일한 성질을 가진 무한번 미분 가능한 함수다.
급수
- 무한번 미분 가능한 함수는 무한 급수로 표현할 수 있다.
- 무한 급수로 표현되는 함수를 통해 오일러 공식의 실마리를 풀어볼 수 있다.
등비수열
- 수열(Sequnce)이란 규칙에 따라 순서에 맞게 수를 나열한 것
- 연속된 항들이 일정한 비(Ratio)로 증가하는 수열을 등비수열(Geometric sequence)이라고 한다.
- 등비수열 규칙에 사용된 비를 공비(Commen ratio)라고 한다.
연속된 두 항이 1/2배씩 증가하는 규칙을 가지므로 공비는 1/2가 된다.
1/2, 1/4, 1/8, 1/16, 1/32, ...- 수열의 첫 번째 값을 초항(First term)이라 부르며 a로 표기한다.
- 공비는 r로, n번째 항은 a_n으로 표시한다.
a_n = a·r^(n-1)- 등비수열의 n + 1번째 항과 n번째 항에 공비를 적용하면 다음과 같은 관계가 성립한다.
a_(n+1) = a_n·r급수
- 수열의 개념을 확장해 수열의 모든 값을 더한 것을 급수(Series)라고 한다.
- 초항 a_0과 n개의 요소로 구성된 수열의 급수는 시그마 기호(Σ)를 활용해 간략히 표현한다.
n
Σ a_k = a_0 + a_1 + a_2 + a_3 + ... + a_n
k=0- 등비수열의 급수는 다음과 같이 표현할 수 있다.
∞
Σ a·r^k
k=0- 등비수열의 급수를 특별히 기하급수(Geometric series)라고 한다.
- 기하급수는 무한대로 계속 증가하거나 특정 수로 수렴하는 성질이 있다.
공비가 1/2인 등비수열의 급수가 어떤 값 s에 수렴한 경우
s = 1/2 + 1/4 + 1/8 + ...
급수 값 s에 공비 1/2를 곱함
1/2·s = 1/2·(1/2 + 1/4 + 1/8 + ...)
위 두 식을 빼보면
1/2·s = 1/2
위 식이 만족하려면 s는 1이어야 하므로 급수 값은 1에 수렴한다.
- 위에서 계산한 기하급수를 구하는 과정을 일반화시켜 정리
등비수열의 초항을 a, 공비가 r이라고 할 때, n개의 유한한 등비급수를 s_n으로 표현
s_n = a + ar + ar^2 + ar^3 + ... + ar^(n-1)
위 식의 양변에 공비 r을 곱함
r·s_n = ar + ar^2 + ar^3 + ... + ar^n
위 두 식을 빼보면
s_n - r·s_n = a - ar^n
좌변을 s_n에 대해 묶으면 다음 식이 유도된다.
s_n(1 - r) = a(1 - r^n)
s_n = a(1 - r^n) / (1 - r)- 기하급수는 무한 개의 요소를 가지므로 위 식의 n에 무한대의 극한을 설정하고 전개
lim s_n = lim a(1 - r^n) / (1 - r)
n->∞ n->∞
= a / (1 - r)·lim (1 - r^n)
n->∞
= a / (1 - r) - a / (1 - r)·lim r^n
n->∞- s_n의 극한값을 구하려면 공비 r이 가질 수 있는 값을 여러 개로 분리하고 각각에 대한 극한을 생각해야 한다.
- 공비 r이 1인 경우 a / (1 - r)의 분모가 0이 되어 극한 값을 구할 수 없다.
- 즉, 기하급수 a를 무한번 더한 식이 되므로 급수 값은 무한대로 발산한다.
- 공비 r이 1이 아니 경우 a / (1 - r)은 상수가 되므로 극한 값은 lim r^n의 값에 따라 결정된다.
- 공비 r의 크기가 1보다 크다면, 공비는 계속 곱할수록 크기도 커져 lim r^n의 극한값을 발산한다.
- 공비 r의 크기가 1보다 작다면, 공비를 계속 곱할수록 그 값의 크기는 계속 작아저 극한값은 0으로 수렴한다.
- 마지막으로 공비 r이 -1이면 lim r^n의 값은 일정한 값을 가지지 못하고 규칙적으로 1과 -1값을 오고간다.
- 이러한 현상을 진동한다(Oscillation)고 표현한다.
- 이 역시 특정 값으로 수렴하지 않으므로 발산으로 취급한다.
- 공비 r의 값에 따른 lim s_n의 성질을 정리하면 다음과 같다.
- r = 1 인 경우에는 발산
- |r| > 1 인 경우에는 발산
- |r| < 1 인 경우에는 수렴
- r = -1 인 경우에는 발산
- 기하급수는 더해지는 모든 항의 계수 a의 값이 모두 같았다.
- 그런데 다음과 같이 항마다 게수가 다른 급수가 존재한다.
- 이를 멱급수(Power series)라고 한다.
∞
Σ a_n·r^n = a_1 + a_2·r + a_3·r^2 + a_4·r^3 + a_5·r^4 + ...
n=0- 기하급수는 모든 계수의 값이 동일한 멱급수의 한 종류라고 할 수 있다.
- 멱급수도 기하급수와 동일하게 특정 조건에 따라 수렴하거나 발산한다.
- 이를 판정하기 위한 비판정법(Ratio test)이 존재한다.
- 비판정법은 멱급수의 항의 계수가 일정한 규칙으로 전개되는 경우, 다음의 극한값을 구해 수렴, 발산 여부를 파악하는 방법이다.
L = lim |a_(n+1) / a_n|
n->∞∞
Σ a·r^n
n=0L = lim |(a·r^(n+1)) / (a·r^n)| = |r|
n->∞∞
Σ r^n / n = x + 1/2·r^2 + 1/3·r^3 + 1/4·r^4 + ...
n=1
이 식에 비판정법을 적용
L = lim |(r^(n+1)/(n+1)) / (r^n/n)|
n->∞
= lim |r|·n/(n+1)
n->∞
= |r|·lim n/(n+1)
n->∞
= |r|·lim ((n+1) - 1)/(n+1)
n->∞
= |r| - |r|·lim 1/(n+1)
n->∞
= |r|f(x) = a_1 + a_2x + a_3x^2 + a_4x^3 + ...f'(x) = 1·a_2 + 2·a_3·x + 3·a_4·x^3 + 4·a_5·x^3 + ...
f''(x) = (2·1)a_3 + (3·2)a_4·x + (4·3)a_5·x^2 + ...
f'''(x) = (3·2·1)a_4 + (4·3·2)a_5·x + ...f(0) = a_1
f'(0) = 1·a_2
f''(0) = (2·1)a_3
f'''(0) = (3·2·1)a_4
...n! = (n - 1)! · n
∴ (n - 1)! = n! / n0! = (1 - 1)! = 1! / 1 = 1f(0) = 0!·a_1
f'(0) = 1!·a_2
f''(0) = 2!·a_3
f'''(0) = 3!·a_4
...a_n = f^(n)(0) / n!f(x) = f(0)/0! + f'(0)/1!·x + f''(0)/2!·x^2 + f'''(0)/3!·x^3 + ...자연지수함수
f(x) = e^x
자연지수함수의 매클로린 급수는 다음과 같이 전개
f(x) = f(0)/0! + f'(0)/1!·x + f''(0)/2!·x^2 + f'''(0)/3!·x^3 + ...
= 1 + x + 1/2!·x^2 + 1/3!·x^3 + ...
∞
= Σ x^n / n!
n=0
자연지수함수에 대응하는 매클로린 급수가 수렴하는지 판단하기 위해 비판정법 진행
L = lim|(x^(n+1)/(n+1)!) / (x^n/n!)|
n->∞
= lim |x|·n!/(n+1)!
n->∞
= |x|·lim 1/(n+1)
n->∞
= |x|·0
= 0
비판정을 진행한 결과는 0이 나오므로 해당 급수는 언제나 수령함
자연지수함수의 매클로린 급수는 유효함
∞
e^x = Σ x^n / n!
n=0
sin 함수
f(x) = sinx
sin 함수의 매클로린 급수는 다음과 같이 전개
f(x) = f(0)/0! + f'(0)/1!·x + f''(0)/2!·x^2 + f'''(0)/3!·x^3 + ...
= 0 + x - 1/3!·x^3 + 1/5!·x^5 + ...
∞
= Σ ((-1)^n·x^(2n+1)) / (2n+1)!
n=0
sin 함수에 대응하는 매클로린 급수가 수렴하는지 판단하기 위해 비판정법 진행
L = lim|((-1)^n+1·x^(2n+3))/(2n+3)! / ((-1)^n·x^(2n+1))/(2n+1)!|
n->∞
= lim |x^2|·((2n+1)!/(2n+3)!)
n->∞
= |x^2|·lim 1/((2n+3)(2n+2))
n->∞
= 0
비판정을 진행한 결과는 0이 나오므로 해당 급수는 언제나 수령함
sin 함수의 매클로린 급수는 유효함
∞
sinx = Σ ((-1)^n·x^(2n+1)) / (2n+1)!
n=0
cos 함수
f(x) = cosx
cos 함수의 매클로린 급수는 다음과 같이 전개
f(x) = f(0)/0! + f'(0)/1!·x + f''(0)/2!·x^2 + f'''(0)/3!·x^3 + ...
= 0 - x - 1/2!·x^2 + 1/4!·x^4 + ...
∞
= Σ ((-1)^n·x^(2n)) / (2n)!
n=0
cos 함수에 대응하는 매클로린 급수가 수렴하는지 판단하기 위해 비판정법 진행
L = lim|((-1)^n+1·x^(2n+2))/(2n+2)! / ((-1)^n·x^(2n))/(2n)!|
n->∞
= lim |x^2|·((2n)!/(2n+2)!)
n->∞
= |x^2|·lim 1/((2n+2)(2n+1))
n->∞
= 0
비판정을 진행한 결과는 0이 나오므로 해당 급수는 언제나 수령함
cos 함수의 매클로린 급수는 유효함
∞
cosx = Σ ((-1)^n·x^(2n)) / (2n)!
n=0cosx + sinx = 1 + x - 1/2!x^2 - 1/3!x^3 + 1/4!x^4 + ...e^(ix) = 1 + ix + 1/2!(ix)^2 + 1/3!(ix)^3 + 1/4!(ix)^4 + ...
= 1 + ix - 1/2!x^2 - i/3!x^3 + 1/4!x^4 + ...e^(ix) = cosx + isinx
x대신 각 Θ를 대입
e^iΘ = cosΘ + isinΘ- 위 식의 우변은 복소평면에서 회전 변환을 담당하는 단위 복소수를 의미한다.
- 오일러 공식의 좌변에 위치한 e^iΘ는 복소평면에서의 회전 변환을 의미한다.
e^iΘ = (cosΘ, sinΘ) = ┌ cosΘ -sinΘ ┐
└ sinΘ cosΘ ┘- 지금까지 행렬과 복소수를 사용해 표현했던 회전변환은 오일러 공식으로 e^iΘ라는 자연지수함수로 더욱 간단하게 표현할 수 있다.
- 각 α, β의 회전 변환은 오일러 공식에 의해 각각 e^iα, e^iβ로 표현할 수 있다.
- 이 둘을 곱하면 (α + β)의 회전 변환이 만들어진다.
- 이는 지수법칙에 의해 자연스럽게 e^(iα + iβ)가 만들어진다.
e^(α + β)i = e^αi·e^βie^iπ = cosπ + isinπ
= -1 + 0
∴ e^iπ + 1 = 0
https://m.yes24.com/Goods/Detail/107025224
이득우의 게임 수학 - 예스24
39가지 실시간 렌더링 게임 프로그래밍 실습 예제를 하나씩 따라 해보며 독자가 직접 체득하는 흥미로운 게임 수학의 세계! 게임 개발자와 그래픽 아티스트들이 궁금해 했던 3D 가상 세계와 메타
m.yes24.com
[Game Math] Chapter 15. 오일러 공식: 허수로 표현하는 회전 변환
이득우의 게임 수학 책을 읽고 공부한 노트입니다.
frompero.github.io
https://wecandev.tistory.com/221
[이득우 게임수학] 15. 오일러 공식 : 허수로 표현하는 회전 변환
15.1 자연지수함수 //오일러 공식 e^iθ = cosθ + i sinθ 무리수 e y = (1 + 1/x)^x e = lim/x->∞ (1 + 1/x)^x 자연 지수 함수 거듭제곱(Exponentiation) : 같은 수를 여러 번 곱하는 작업 지수(Exponent) : 거듭제곱에서
wecandev.tistory.com
'게임수학' 카테고리의 다른 글
| [게임수학] 캐릭터 구축 (0) | 2024.05.08 |
|---|---|
| [게임수학] 사원수(Quaternion) (0) | 2024.05.06 |
| [게임수학] 복소수 (1) | 2024.05.03 |
| [게임수학] 모델링과 뷰 (0) | 2024.04.28 |
| [게임수학] 절두체(Frustum) (0) | 2024.04.25 |
