사원수 대수
- 사원수는 복소수와 동일하게 허수를 사용하는 수의 집합이다.
- 사원수는 하나의 실수부와 세 개의 허수부로 구성된다.
- 총 4가지 수체계를 사용하기 때문에 사원수라고 한다.
- 사원수에서는 세 허수부를 구성하는 단위를 각각 i, j, k로 표시한다.
사원수를 구성하는 세 허수
- 사원수는 3개의 허수부 i, j, k로 구성되어 있지만 이들은 모두 복소수의 허수 단위 i와 같은 성질을 가진다.
i^2 = -1
i^2 = j^2 = k^2 = -1- 세 허수 중에서 두 허수의 곱은 다음과 같이 나머지 다른 허수에 대응된다.
- 이들은 회전의 순환 순서 x -> y -> z -> x와 유사하게 i -> j -> k -> i 순서로 대응된다.
ij = k
jk = i
ki = j- 위 식으로부터 ij의 값은 k가 되고 kk의 결과는 -1이므로 ijk = -1이라는 식이 성립한다.
각 세 허수의 곱셈의 결과
ijk = jki = kij = -1- 복소수가 a + bi의 형태를 가졌던 것 처럼 사원수도 실수부와 허수부를 덧셈으로 묶고 실수를 사용해 허수부의 계수를 지정한다.
- 실수부와 각 허수부의 계수를 a, b, c, d로 지정한 사원수는 다음과 같이 표현한다.
q = a + bi + cj + dk- 사원수의 집합 기호는 H다.
- 사원수는 복소수와 유사하게 덧셈과 곱셈이 존재하며, 체와 유사한 구조를 지닌다.
사원수의 구조
- 사원수의 덧셈은 복소수와 유사하게 실수부와 각 허수부끼리 더하는 형태로 진행된다.
q_1 + q_2 = (a_1 + a_2) + (b_1 + b_2)i + (c_1 + c_2)j + (d_1 + d_2)k- 사원수의 덧셈이 만족하는 성질은 다음과 같다.
1. 결합법칙
q_1 + (q_2 + q_3) = (q_1 + q_2) + q_3
= (a_1 + a_2 + a_3) + (b_1 + b_2 + b_3)i + (c_1 + c_2 + c_3)j + (d_1 + d_2 + d_3)k
2. 교환법칙
q_1 + q_2 = q_2 + q_1 = (a_1 + a_2) + (b_1 + b_2)i + (c_1 + c_2)j + (d_1 + d_2)k
3. 항등원
(a + bi + cj + dk) + (0 + 0i + 0j + 0k) = (a + bi + cj + dk)
4. 역원
(a+ bi + cj + dk) + (-a - bi - cj - dk) = (0 + 0i + 0j + 0k)- 사원수의 곱셈은 해밀턴 곱(Hamlton product)으로 불리며 모든 요소를 교차해 곱하는 방식으로 진행된다.
- 사원수는 총 4가지 요소로 구성되므로 곱의 결과는 총 16가지 인자가 만들어진다.
q_1·q_2 = (a_1·a_2 - b_1·b_2 - c_1·c_2 - d_1·d_2)
+ (a_1·b_2 + a_2·b_1 + c_1·d_2 - d_1·c_2)i
+ (a_1·c_2 + a_2·c_1 + b_2·d_1 - b_1·d_2)j
+ (a_1·d_2 + a_2·d_1 + b_1·c_2 - c_1·b_2)k- 사원수 곱셈이 만족하는 성질은 다음과 같다.
1. 결합법칙
q_1·(q_2·q_3) = (q_1·q_2)·q_3
2. 분배법칙
q_1·(q_2 + q_3) = q_1·q_2 + q_1·q_3
3. 항등원
(a + bi + cj + dk)·(1 + 0i + 0j + 0k) = (a + bi + cj + dk)- 사원수 곱셈은 순서를 바꿔 계산하면 결과가 달라진다.
q_2·q_1 = (a_1·a_2 - b_1·b_2 - c_1·c_2 - d_1·d_2)
+ (a_1·b_2 + a_2·b_1 - c_1·d_2 + d_1·c_2)i
+ (a_1·c_2 + a_2·c_1 - b_2·d_1 + b_1·d_2)j
+ (a_1·d_2 + a_2·d_1 - b_1·c_2 + c_1·b_2)k- 사원수 곱셈은 교환법칙이 성립하지 않아 체의 구조를 가지고 있지 않지만 결합법칙 등 나머지 체의 성질은 모두 만족한다.
- 체의 구조에서 교환법칙이 성립하지 않는 구조를 유사체(Skew field)라고 한다.
- 사원수는 유사체의 구조를 가진다.
- 사원수끼리 곱셈식을 전개할 때는 왼쪽과 오른쪽의 순서가 바뀌지 않도록 주의해야 한다.
- 사원수의 크기는 복소수와 동일하게 각 계수를 제곱한 값을 더하고 제곱근을 취해 계산한다.
- 절대값 기호 | |를 써서 표기
- 사원수의 크기 역시 노름(Norm)이라 부른다.
|q| = sqrt(a^2 + b^2 + c^2 + d^2)- 사원수 중에서 크기가 1인 사원수를 단위 사원수(Unit quaternion)라고 한다.
- 사원수의 세 허수부의 계수에 음수를 적용한 사원수를 켤레 사원수라고 부르고 q^*로 표기하며 다음과 같이 표현
q^* = a - (bi + cj + dk)- 사원수와 켤레 사원수의 곱은 복소수와 켤레 복소수 간의 곱의 성질과 동일하다.
(q^*)^* = q
(p·q)^* = q^*·p^*- 임의의 사원수에 그 켤레를 곱하면 크기의 제곱 값이 나온다.
q^*·q = q·q^* = a^2 + b^2 + c^2 + d^2 = |q|^2
위 식을 통해 단위 사원수와 그 켤레의 곱은 언제나 1이 되는 것을 알 수 있다.- 사원수도 복소수와 동일하게 켤레 사원수의 성질을 사용해 사원수 곱의 역원을 유도할 수 있다.
q^-1 = 1/q = q^* / (q·q^*) = q^* / |q|^2
위 식을 통해 크기가 1인 단위 사원수의 곱셈의 역원은 켤레 사원수가 됨을 알 수 있다.사원수와 벡터
- 4개의 요소를 사용하는 사원수는 4개의 수 집합이 직교하는 4차원의 공간으로 시각화 할 수 있다.
- 하지만 4차원 공간은 인지범위를 넘어서기 때문에 이를 시각적으로 정확하게 표현하는 것은 불가능하다.
- 사원수를 다룰 때에는 4차원 공간을 1차원과 3차원으로 분리하고 3차원 공간의 성질을 관찰하는 것이 더욱 효과적
- 사원수를 다룰때에는 허수부를 사용하는 3개의 수 집합을 하나로 묶고, 나머지 실수부는 별도로 관리하는 방법을 사용
- 세 허수부의 계수를 3차원 벡터로 묶는다면, 사원수는 실수와 3차원 벡터 두 가지 요소로 구성된다고 볼 수 있다.
q = w + xi + yj + zk = (w, v)- 위 순서쌍의 원소를 차례대로 실수부, 허수부라고 한다.
- 이들을 각각 스칼라부, 벡터부라고도 부른다.
- 3차원 벡터를 사용해 사원수를 표현하면 사원수의 연산을 좀 더 체계적으로 정리할 수 있다.
1. 사원수의 덧셈
q_1 + q_2 = (w_1 + w_2, v_1 + v_2)
2. 사원수의 곱셈
벡터의 내적과 외적을 사용해 표현할 수 있다.
q_1·q_2 = (w_1w_2 - (v_1·v_2), w_1v_2 + w_2v_1 + v_1 x v_2)
위 식을 통해 사원수의 곱셈은 교환법칙이 성립하지 않음을 확인할 수 있다.
벡터 연산이 교환법칙이 성립하지 않는 외적이 관련되어 있기 때문- 사원수에서 실수부가 0인 사원수를 특별히 순허수 사원수(Pure Imaginary quaternion)라고 부른다.
- 순허수 사원수는 세 허수로만 구성된 수를 말한다.
- 이는 3차원 벡터 공간에 대응되는 개념
- 3차원 공간이 사원수를 다루는 4차원 공간의 일부라면, 3차원 공간의 벡터는 다음 순허수 사원수에 대응된다.
xi + yj + zk = (0, v)- 순허수 사원수의 곱셈을 전개하면 다음과 같다.
q_1·q_2 = (-v_1·v_2, v1 x v_2)
w_1과 w_2의 값이 0이므로 이들이 포함된 항의 값은 모두 0이 된다.
곱셈의 결과는 내적과 외적만 남게 된다.사원수의 회전
- 자연지수함수, sin 함수, cos 함수를 매클로린 급수로 전개했을 때 세 급수가 서로 통합되기 위해서는 크기가 1이고, 제곱한 수가 -1이 되는 특별한 수가 필요함을 알 수 있었다.
- 복소수 체계에서 이 조건을 만족하는 특별한 수인 허수 i를 사용해 다음의 오일러 공식을 전개할 수 있었다.
e^(iΘ) = cosΘ + isinΘ = (cosΘ, sinΘ)- 사원수에서도 허수 i와 동일하게 크기가 1이고 제곱한 값이 -1인 수가 있다면 오일러 공식을 만족할 것
사원수와 오일러 공식
- 순허수 사원수는 크기가 1이고, 제곱한 값이 -1이다.
- 크기가 1인 순허수 사원수를 q_n으로 지정하고, 요소를 (0, n)으로 표시하면 다음 식이 성립한다.
sqrt(0 + |n|^2) = 1- 위 식을 통해 n의 크기도 1이 됨을 알 수 있으며, 내적 n·n의 값도 1이 된다.
|n| = n·n = 1- 순허수 사원수 q_n의 제곱을 전개하면 다음과 같다.
q_n^2 = q_n·q_n = (-n·n, n x n)
n·n은 1이고 평행한 벡터의 외적은 영벡터가 되므로 다음과 같이 간략화된다.
q_n·q_n = (-1, 0)- 위 식을 통해 크기가 1인 순허수 사원수를 제곱한 결과는 -1이 됨을 확인할 수 있다.
- 따라서 오일러 공식의 전개 과정에서 허수 i대신 순허수 사원수의 벡터 n을 사용할 수 있다.
- 자연상수의 지수함수로 사원수의 회전을 표현하는 것이 가능한 것을 알 수 있음
e^(RΘ) = cosΘ + sinΘ·n = (cosΘ, sinΘ·n)- (cosΘ, sinΘ·n) 형태의 사원수는 4차원 공간에서 회전축 n을 중심으로 회전 변환하는 성질을 가진다.
- 이를 회전 사원수(Rotation quaternion)라고 한다.
- 회전 사원수를 q, 벡터 n의 요소를 (a, b, c)로 표기하고 이를 확인하면 다음과 같다.
q = cosΘ + sinΘ·n = cosΘ + sinΘ(ai + bj + ck)
|q| = cos^2Θ + sin^Θ(a^2 + b^2 + c^2) = 1
벡터 n의 크기가 1인 단위 벡터이므로 a^2 + b^2 + c^2 = 1의 조건에 의해
위와 같이 전개되는 것을 알 수 있다.
따라서 회전 사원수는 언제나 단위 사원수임을 알 수 있다.- 회전 사원수의 켤레는 다음과 같이 표현한다.
q^* = (cosΘ, -sinΘ·n)
이는 반대 방향의 회전을 의미한다.
q^* = (cos(-Θ), sin(-Θ)·n)- 반대 방향의 회전을 의미하는 회전 사원수의 켤레 사원수는 오일러 공식으로도 확인할 수 있다.
- 단위 사원수와 그 켤레를 곱한 값은 언제나 1이 나옴을 확인 하였다.
- 이를 자연지수함수로 표현하면 0의 지수로 나타낼 수 있다.
q·q^* = 1 = e^0- 오일러 공식에 의한 회전 사원수에 대응하는 지수함수는 다음과 같았다.
q = e^(nΘ)- 이를 회전 사원수 q에 치환한 식은 다음과 같이 전개된다.
e^(nΘ)·q^* = e^0- 위 식을 만족하는 q^* 의 값은 e^-(nΘ)이며 이는 같은 축 n을 중심으로 반대 방향으로 Θ만큼 돌리는 회전을 의미함
q^* = e^-(nΘ) = e^(n(-Θ))3차원 공간에서의 회전
- 일반적으로 사용하는 3차원 공간의 벡터 v는 순허수 사원수에 대응되는 개념이다.
벡터 v = (x, y, z), 회전축 n = (a, b, c)
회전축은 단위 벡터이므로 a^2 + b^2 + c^2 = 1의 조건을 가짐
회전축 n으로 각 Θ만큼 회전시키는 회전 사원수 q = (cosΘ, sinΘ·n)의 값을 자김- 회전 사원수 q를 사용해 벡터를 회전시키는 방법은 회전 사원수를 벡터의 왼쪽에 배치하고 둘을 곱하는 것임
- 회전 사원수와 순허수 사원수 벡터 v의 곱셈은 다음과 같다.
q·v = (cosΘ, sinΘ·n)·(0, v)
= (-sinΘ(n·v), cosΘv + sinΘ(n x v))- 위 식을 살펴보면 회전 사원수와 벡터를 곱한 결과는 순허수 사원수가 아닌 네 요소를 모두 사용하는 일반 사원수가 나온다.
- 따라서 이 곱의 결과는 순허수 사원수와 1:1로 대응했던 3차원 공간의 규격에서 벗어나게 되므로 3차원 공간의 요소로 사용할 수 없게 된다.
- 3차원 공간에서 벡터를 회전시키는 용도로 사원수를 사용하기 위해서는 사원수 곱의 결과가 항상 순허수 사원수가 되는 특별한 수식을 찾아야 한다.
- 회전 사원수 벡터 n은 회전축의 역할을 수행한다.
- 이는 로드리게스 회전 공식에서 언급된 축-각 회전에 대응하는 벡터다.
- 3차원 공간에서 임의의 축 n에 대한 회전을 표현하면 아래 그림과 같다.

- 회전시킬 벡터를 v로 지정하고 이를 회전축 n에 평행한 성분과 수직인 성분으로 나누면 다음과 같은 식이 성립한다.
회전축에 수평인 성분을 v_||, 수직인 성분을 v_⊥으로 표시
v = v_|| + v_⊥
- 위 그림은 벡터 v를 수직 성분과 수평 성분으로 분리해 나타낸 그림이다.
- 이를 각 Θ만큼 회전 시킨 벡터를 v^'라고 한다.

- 최종 회전의 벡터 v^'는 위 그림과 같이 회전축에 수직인 성분만 회전시킨 후, 수평 성분을 그대로 더하면 구할 수 있다.
- 3차원 공간에서의 회전은 다음과 같은 식이 될 것이다.
v' = v_|| + q·v_⊥- 오일러 공식을 활용해 위 수식을 정리하면 다음과 같다.
v' = v_|| + e^(nΘ)·v_⊥
우변의 두번째 항인 회전 사원수와 벡터와의 곱셈은 다음과 같이 전개된다.
e^(nΘ)·v_⊥ = (-sinΘ(n·v_⊥), cosΘv_⊥ + sinΘ(n x v_⊥))
= (0, cosΘv_⊥ + sinΘ(n x v_⊥))- 회전축에 수직인 벡터와 회전 사원수의 곱으로 얻어지는 사원수는 항상 실수부 값이 0인 순허수 사원수가 되므로, 이의 결과는 언제나 3차원 공간의 벡터에 대응됨을 확인할 수 있다.
- 3차원 공간의 회전식을 간략하게 정리하도록 연산 순서를 바꿔 전개
연산 순서를 변경하면 외적의 성질에 의해 sin 함수의 부호가 바뀐다.
v_⊥·e^(nΘ) = (0, cosΘv_⊥ - sinΘ(n x v_⊥))
회전각에 -Θ를 대입
v_⊥·e^(n(-Θ)) = (0, cos(-Θ)v_⊥ - sin(-Θ)(n x v_⊥))
= (0, cosΘv_⊥ + sinΘ(n x v_⊥))
두 항의 순서를 바꿔 연산한 결과는 처음 식과 동일함
이는 회전축과 직교하는 벡터에 대해서 다음과 같은 식이 성립함을 알 수 있다.
e^(nΘ)·v_⊥ = v_⊥·e^(n(-Θ))- 회전축에 평행한 벡터 v_|| 의 회전 사원수 곱이 가지는 성질
평행인 두 벡터의 외적은 영벡터가 되므로 실수부가 남고 허수부가 단순화된다.
e^(nΘ)·v_|| = (-sinΘ(n·v_||), cosΘv_||)
사원수 곱에서 교환법칙의 성립을 방해하던 외적 부분이 사라졌기 때문에
평행인 벡터와의 곱은 항상 교환법칙이 성립한다.
e^(nΘ)·v_|| = v_||·e^(nΘ)
식을 단순화 좀 더 단순화 하기 위해, 회전 사원수를 둘로 쪼개서 나타내보자
각 Θ의 회전을 수행하는 회전 사원수는 이를 절반 나눈 각 Θ/2의 회전 사원수를 두 번 곱한 결과와 동일함
e^(nΘ) = e^(n(Θ/2))·e^(n(Θ/2))
회전 사원수와 그 켤레 사원수와의 곱은 아무런 변화 없는 0° 회전을 만들어낸다.
따라서 이들의 곱은 곱셈의 항등원 1에 대응된다.
1 = e^0 = e^(n(Θ/2))·e^(n(-Θ/2))
이를 활용해 3차원 공간에서의 회전을 전개하면 다음과 같이 정리된다.
v' = v_|| + e^(nΘ)·v_⊥
= e^0·v_|| + e^(nΘ)·v_⊥
= e^(n(Θ/2))·e^(n(-Θ/2))·v_|| + e^(n(Θ/2))·e^(n(Θ/2))·v_⊥
= e^(n(Θ/2))·v_||·e^(n(-Θ/2)) + e^(n(Θ/2))·v_⊥·e^(n(-Θ/2))
= e^(n(Θ/2))·(v_|| + v_⊥)·e^(n(-Θ/2))
= e^(n(Θ/2))·v·e^(n(-Θ/2))
간략화된 최종 식에서 자연지수함수를 다시 사원수 형태로 바꿔보면 다음과 같다.
Θ/2만큼 돌리는 회전 사원수를 q로 표현. 반대 방향으로 돌리는 사원수는 켤레 사원수 q^*
e^(n(Θ/2)) = q- 3차원 공간의 회전을 보장하는 사원수 회전식은 다음과 같이 최종 정리된다.
v' = e^(n(Θ/2))·v·e^(n(-Θ/2))
= q·v·q^*- 회전 사원수에 사용한 각은 Θ/2이므로 여기에 사용한 사원수 q의 값은 다음과 같다.
q = (cosΘ/2, sinΘ/2·n)- 절반의 각만 회전시키는 단위 사원수를 임의의 벡터와 곱했을 때 그 결과가 항상 실수부가 0인 순허수 사원수가 나오는지 확인
회전 사원수 q의 실수부와 허수부를 각각 w와 r로 표시
q = (cosΘ/2, sinΘ/2·n) = (w, r)
3차원 공간의 회전을 보장하는 사원수 회전식을 내적과 외적의 형태로 바꿔서 전개
v' = q·v·q^*
= (w, r)·(0, v)·(w, -r)
= (-(r·v), wv+(r x v))·(w, -r)
= (-(r·v)w - (wv+(r x v))·(-r), -(r·v)·(-r)+w(wv + (r x v))+(wv + (r x v)) x (-r))
위 식에서 실수부와 허수부를 다음과 같이 각각 따로 전개
첫 항인 실수부를 전개하면 다음과 같다.
-(r·v)w - (wv+(r x v))·(-r) = -(r·v)w + w(v·r) + (r x v)·r
= -(r·v)w + w(v·r)
= -(r·v)w + (r·v)w
= 0
3차원 공간의 회전을 보장하는 식을 내적과 외적으로 전개했을 때 실수부 값은 언제나 0이 나온다.
이는 절반의 각과 그 켤레를 사용해 회전시킨 결과가 항상 3차원 공간의 벡터에 대응된다고 할 수 있다.
허수부의 수식을 전개하면 다음과 같다.
v' = -(r·v)·(-r)+w(wv + (r x v))+(wv + (r x v)) x (-r)
= (r·v)·r + w^2v + w(r x v) - w(v x r) - (r x v) x r
= (r·v)·r + w^2v + 2w(r x v) - (r x v) x r
= (r·v)·r + (1 - r·r)·v + 2w(r x v) - (r x v) x r
= v + (r·v) - (r·r)·v + 2w(r x v) - (r x v) x r
= v + r x (r x v) + 2w(r x v) - (r x v) x r
= v + 2w(r x v) + 2(r x (r x v))- 위 허수부 수식의 최종 값에서 2(r x v)를 벡터 t로 치환하면 다음과 같이 단순하게 정리된다.
v' = v + wt + r x t- 위 수식을 Θ/2가 아닌 각 Θ를 중심으로 전개하면 로드리게스 회전 공식이 유도된다.
v' = v + 2w(r x v) + 2(r x (r x v))
= v + 2cos(Θ/2)(sin(Θ/2)(n x v)) + 2(sin(Θ/2)n x (sin(Θ/2)n x v))
= v + 2cos(Θ/2)sin(Θ/2)(n x v) + 2sin^2(Θ/2)(n x (n x v))
= v + sin(Θ/2 + Θ/2)(n x v) + (1 - cos(Θ/2 + Θ/2))(n x (n x v))
= v + sinΘ(n x v) + (1 - cosΘ)((n·v)n - (n·n)v)
= v - (1 - cosΘ)(n·n)v + sinΘ(n x v) + (1 - cosΘ)(n·v)n
= cosΘv + (1 - cosΘ)(n·v)n + sinΘ(n x v)- 회전 사원수의 벡터부에서 설정한 벡터 n은 축-각 회전에서 회전축의 기능을 수행하는 사실을 확인할 수 있다.
- 또한 각 Θ를 기준으로 전개했을 때 보다 각 Θ/2를 기준으로 전개했을 때 식이 더 간편해진다는 것도 알 수 있다.
- 같은 회전축에 두 개의 다른 각을 연속해서 회전시키는 경우
첫 번째 각의 크기를 2α, 두 번째 각의 크기를 2β로 지정
회전할 벡터를 v, 첫 번째 회전을 적용한 벡터를 v', 두 번째 회전을 적용한 벡터를 v''로 표기
v' = q_α·v·q_α
v'' = q_β·v'·q_β
벡터 v'를 q_α·v·q_α로 치환하면 v''를 계산하는 식은 다음과 같이 전개
v'' = q_β·(q_α·v·q_α)·q_β
= (q_β·q_α)·v·(q_α·q_β)
= (q_β·q_α)·v·(q_β·q_α)^*
= q_(α+β)·v·q_(α+β)^*- 3차원 공간의 회전을 위해 절반의 각과 켤레 사원수를 사용하더라도 서로 다른 두 회전 사원수의 곱은 두 각을 합한 회전 사원수와 형태가 동일하다는 점을 알 수 있다.
- 회전 사원수와 회전 사원수의 곱은 두 각을 합한 사원수에 대응되며, 사원수와 3차원 벡터의 곱은 사원수로 표현된 회전축과 각으로 벡터를 회전시킨 결과에 대응한다.
사원수의 변환
- 사원수를 활용해 3차원 벡터를 회전시키는 방법을 알고 있지만, 사원수를 구성하는 요소 값은 직관적이지 않아 회전을 설계할 때 어려움이 따른다.
- 3차원 공간에서 물체를 회전을 설정할 때에는 오일러 각 방식이 사원수보다 직관적이고 편리하기 때문에, 오일러 각의 값을 사원수로 변환해주는 방법을 알고 있다면 게임 제작에 유용하게 사용할 수 있다.
오일러 각에서 사원수로의 변환
- 오일러 각의 각 회전은 x, y, z 기저 축이 회전축의 역할을 수행한다.
- 3차원 공간에서 x축을 중심으로 각 Θ만큼 회전시키는데 사용하는 회전 사원수 q는 다음과 같다.
q = (cos(Θ/2), sin(Θ/2)·x) = cos(Θ/2) + sin(Θ/2)i- 오일러 각을 구성하는 Roll, Pitch, Yaw 회전에 대응하는 각 사원수는 다음과 같이 표현된다.
q_roll = cos(Θ_roll/2) + sin(Θ_roll/2)k
q_pitch = cos(Θ_pitch/2) + sin(Θ_pitch/2)i
q_yaw = cos(Θ_yaw/2) + sin(Θ_yaw/2)j- 오일러 각의 회전 순서는 Roll, Pitch, Yaw 순서로 적용된다.
- 대응하는 사원수를 동일한 순서에 맞춰서 곱하면 오일러 각에 대응하는 사원수가 만들어진다.
q_roll·q_pitch·q_yaw = cos(Θ_roll/2) cos(Θ_pitch/2) cos(Θ_yaw/2)
+ sin(Θ_roll/2) sin(Θ_pitch/2) sin(Θ_yaw/2) +
(cos(Θ_roll/2) sin(Θ_pitch/2) cos(Θ_yaw/2)
+ sin(Θ_roll/2) cos(Θ_pitch/2) sin(Θ_yaw/2))i +
(cos(Θ_roll/2) cos(Θ_pitch/2) sin(Θ_yaw/2)
- sin(Θ_roll/2) sin(Θ_pitch/2) cos(Θ_yaw/2))j +
(sin(Θ_roll/2) cos(Θ_pitch/2) cos(Θ_yaw/2)
- cos(Θ_roll/2) sin(Θ_pitch/2) sin(Θ_yaw/2))k사원수에서 오일러 각으로의 변환
- 사원수로부터 오일러 각의 값을 변환하는 방법은 조금 복잡하다.
- 오일러 각에서 사원수로 변환하는 식에서 실수부를 w, 각 허수부 값을 x, y, z로 치환한다.
- 이후 2(wz + xy)를 계산한 결과를 살펴보면 알 수 있다.
- 요, 롤, 피치의 절반각을 y, r, p로 표기하고, 이들의 sin 값을 sy, sr, sp로 지정하고 cos 값을 cr, cp, cy로 지정해 식을 전개
w = cr·cp·cy + sr·sp·sy
z = cr·cp·cy - sr·sp·sy
wz = cy^2·cr·cp^2·sr - cy·cr^2·cp·sy·sp + cy·cp·sy·sr^2·sp - cr·sy^2·sr·sp^2
x = sy·sr·cp + sp·cy·cr
y = sy·cp·cr - sp·sr·cy
xy = cr·cp^2·sy^2·sr - cy·cp·sy·sr^2·sp + cy·cr^2·cp·sy·sp - cy^2·cr·sr·sp^2- 사원수로부터 오일러 각을 구하려면 사원수를 잘 조합해 단일 각에 대한 삼각함수가 나오도록 식을 설정해야한다.
- 롤 회전에 대한 삼각함수를 만들어주는 wz + xy의 값을 계산하면 다음과 같다.
wz + xy = cr·cp^2·sr - (cy·cp·sy·sp) + cy·cp·sy·sp - (cr·sr·sp^2)
= cr·sr(cp^2 - sp^2)
= (sin(2r)/2)·cos(2p)- 2(wz + xy)의 값은 sinΘ_roll · cosΘ_pitch가 된다.
- 같은 방식으로 1 - 2(z^2 + x^2)를 계산하면 cosΘ_roll · cosΘ_pitch가 된다.
- sinΘ_roll · cosΘ_pitch값을 cosΘ_roll · cosΘ_pitch로 나누면 다음과 같이 롤 회전의 tan 값이 나온다.
sinΘ_roll·cosΘ_pitch / cosΘ_roll·cosΘ_pitch = tanΘ_roll
= 2(wz + xy) / (1 - 2(z^2 + x^2))- 롤 회전 값은 arctan 함수를 사용해 구할 수 있다.
Θ_roll = atan2(2(wz + xy), 1 - 2(z^2 + x^2))- 피지 회전에 대한 삼각함수를 만들어주는 wx - yz값은 다음과 같이 전개된다.
wz - xy = (sin(Θ_pitch)/2)·(cos(Θ_pitch)/2)
= 1/2(sinΘ_pitch)
따라서 피치 회전각은 arcsin 함수를 사용해 구할 수 있다.
Θ_pitch = asin(2(wx - yz))- asin 함수의 정의역은 [-1, 1] 범위로 제한되어 있으므로 wz - yz 값이 [-0.5, 0.5] 범위를 벗어나지 않는지 확인하고 벗어나는 경우 범위내 가장 가까운 값으로 설정해야 한다.
- 요 회전은 롤 회전과 유사한 방법으로 요 회전의 tan 함수 값을 구한 후 arctan 함수를 사용한다.
Θ_yaw = atan2(2(wy + xz), 1 - 2(x^2 + y^2))사원수에서 회전 변환행렬로의 변환
- 회전 변환행렬은 로컬 축으로 구성되어 있기 떄문에 사원수를 사용해 회전된 세 로컬 축의 값을 구하면 쉽게 해결할 수 있다.
- 사원수를 구성하는 네 요소를 x, y, z, w라고 할 때 벡터 r의 값은 (x, y, z)가 되고 여기에 회전시킬 벡터 값을 v에 대입하면 외적 식으로 회전된 벡터 값을 계산할 수 있다.
- 먼저 회전할 벡터는 x축 기저 벡터 (1, 0, 0)이다.
- 이를 계산한 결과는 사원수에 의해 회전된 x로컬 축을 의미한다.
x_local = (1, 0, 0) + w(0, 2z, -2y) + (x, y, z) x (0, 2z, -2y)
= (1, 2zw, -2yw) + (-2y^2 - 2z^2, 2xy, 2xz)
= (1 - 2(y^2 + z^2), 2(xy + zw), 2(wz - yw)- 마찬가지로 동일한 사원수에 벡터 (0, 1, 0), (0, 0, 1)을 곱하면 각각 다음 식이 나온다.
y_local = (2(xy - zw), 1 - 2(x^2 + z^2), 2(yz + xw))
z_local = (2(xz + yw), w(yz - xw), 1 - 2(x^2 + y^2))- 모든 로컬 축을 구했다면, 이들을 행렬에 넣으면 회전 변환 행렬을 만들 수 있다.
┌ 1 - 2(y^2 + z^2) 2(xy - zw) 2(xz + yw) ┐
| 2(xy + zw) 1 - 2(x^2 + z^2) w(yz - xw) |
└ 2(wz - yw) 2(yz + xw) 1 - 2(x^2 + y^2) ┘회전 변환행렬에서 사원수로 변환
- 행렬의 요소를 조합해서 사원수를 구성하는 x, y, z, w 값을 개별로 구하는 방법을 찾아야 한다.
- 이는 정방행렬의 모든 대각 성분의 합을 더하는 것에서 실마리를 찾을 수 있다.
- 정방행렬의 대각 성분을 모두 더한 값을 트레이스(Trace)라고 한다.
- 사원수에서 회전 변환행렬로 변환한 행렬의 대각행렬 값을 모두 더한 트레이스 t는 다음과 같이 계산된다.
t = 1 - 2(y^2 + z^2) + 1 - 2(x^2 + z^2) + 1 - 2(x^2 + y^2)
= 3 - 4(x^2 + y^2 + z^2)- 위 식에 1을 더하면 제곱근을 씌울 수 있는 형태가 나온다.
- 크기가 1인 회전 사원수의 성질에 의해 x^2 + y^2 + z^2의 값은 1 - w^2이 된다.
- 따라서 트레이스 값은 4w^2이 된다.
t + 1 = 4 - 4(x^2 + y^2 + z^2) = 4w^2- 위 식에 제곱근을 씌운 값에서 양수 값을 r로 지정하면 r과 트레이스 t와의 관계는 다음과 같다.
r = 2w = sqrt(t + 1)- 사원수 w값은 다음과 같이 구할 수 있다.
w = 1/2(r)- 위에서 구한 w값을 이용해 나머지 값 x, y, z를 구할 수 있다.
- 회전 변환행렬을 살펴보면 대각 방향으로 대칭된 행렬 요소를 서로 빼면 두 사원수 요소의 곱으로 정리된다.
두 번째 열 벡터의 세 번째 요소에서 세 번째 열벡터의 두 번째 요소를 빼면
2yz + 2xw - 2yz + 2xw = 4wx
세 번째 열벡터의 첫 번째 요소에서 첫 번째 열벡터의 세 번째 요소를 빼면
2xz + 2yw - 2xz + 2yw = 4yx
첫 번째 열벡터의 두 번째 요소에서 두 번째 열벡터의 첫 번째 요소를 빼면
2xy + 2zw - 2xy + 2zw = 4zw- 이 방식으로 사원수를 구할때는 예외 사항이 있다.
- 트레이스 값이 -1보다 작거나 같으면 제곱근을 구하는 값이 0보다 작거나 같아져 w를 구하는데 필요한 r의 해가 존재하지 않는다.
y축으로 180도 회전하는 행렬은 x 기저와 z 기저를 반대 방향으로 돌리므로 다음과 같이 구성된다.
┌ -1 0 0 ┐
| 0 1 0 |
└ 0 0 -1 ┘
이 행렬을 사용하는 경우 트레이스 값은 -1이 되고 w 값은 0이 된다.
0의 역수는 존재하지 않기 떄문에 나머지 값들을 구할 수 없다.
이러한 경우, w가 아닌 다른 요소로부터 계산한 후, 이로부터 다른 성분을 구하도록 방법을 우회해야 한다.
주어진 회전 변환행렬에서 첫 번째 대각 성분과 두 번쨰와 세 번째 대각 성분을 빼면 다음과 같다.
1 - 2y^2 - 2z^2 - 1 + 2x^2 + 2z^2 - 1 + 2x^2 + 2y^2 = -1 + 4x^2
위 방법을 통해 x 값을 구할 수 있다.
y값은 두 번째 대각 성분에 첫 번째와 세 번째를 빼서 얻을 수 있다.
z값은 세 번째 대각 성분에 첫 번째와 두 번쨰를 빼서 얻을 수 있다.- 예외 상황을 감안해 회전 변환 행렬로부터 사원수를 구하는 알고리즘이 1985년 켄 슈메이크에 의해 고안됐다.
- 먼저 회전 변환행렬의 트레이스 값을 구하고 그 값이 충분히 큰지 파악한다.
- 이론적으로 트레이스 값이 -1보다 크면 w 값 계산이 가능하지만, -1에 가까워질수록 오차가 발생히므로 트레이스 값이 0보다 큰 경우에만 대칭된 요소를 서로 뺀 로직을 적용한다.
- 나머지 트레이스 값이 0보다 작거나 같은 경우에는 예외 상황으로 간주해 다른 값부터 구하는 것이 알고리즘의 핵심
- w를 제외하고 x, y, z 중에서 가장 큰 요소를 파악한다.
- 각 대각행렬의 요소 값을 비교하면 확인할 수 있다.
- 예를 들어 대각행렬의 첫 번째 대각 요소와 두 번째 대각 요소의 크기를 비교했을 때 두 번째 요소 값이 크다면 y의 크기가 x보다 크다는 의미
1 - 2(y^2 + z^2) < 1 - 2(x^2 + z^2)
-y^2 < -x^2- 이 과정을 한번 더 거치면 x, y, z에서 가장 큰 요소를 찾을 수 있다.
- 이렇게 파악된 가장 큰 요소의 값을 먼저 구한다.
- 이와 같은 방법으로 가장 큰 수를 구했다면 나머지 두 요소는 xy, yz, xz 값으로부터 얻을 수 있다
사원수의 보간
- 사원수는 로드리게스 회전과 동일한 축-각 방식을 사용해 3차원 공간의 회전을 표현한다.
- 사원수를 사용하는 경우의 장점은 다음과 같다.
- 오일러 각과 쉽게 변환이 가능하며 회전행렬 제작이 용의하다.
- 임의의 축에 대한 회전 표현이 가능하기 때문에 짐벌락 현상을 방지할 수 있다.
- 임의의 축에 대한 회전 보간 값을 구할 수 있다.
- 4개의 숫자로 회전을 표현하기 때문에 저장 공간을 효율적으로 쓸 수 있다.
- 또한 사원수는 행렬과 상호 변환이 가능하다.
- 다른 회전 방식에 비해 사원수가 가지는 장점은 회전 보간이 가능하다는 것이다.

- 사원수를 4차원 공간의 벡터로 생각하고, 두 사원수가 만들어내는 4차원 공간에서의 평면을 상상하면
- 해당 평면에서 주어진 비율 t에 대응하는 사원수는 두 사원수의 위치를 선형 보간한 지점이 된다.
- 두 사원수가 만든 평면에서 1/3만큼 보간된 사원수를 구하는 방법은 위 그림과 같이 계산할 수 있다.
주어진 비율 t에 대응하는 중간 사원수를 구하는 수식
q(t) = (1 - t)·q_1 + t·q_2- 선형 보간으로 얻어지는 사원수는 크기가 1인 단위 사원수가 아니기 때문에 해당 사원수를 회전에 사용하려면 정규화 과정을 거쳐야 한다.
q' = q(t) / |q(t)|- 선형 보간법은 빠르고 간편하게 사용할 수 있지만, 원의 궤적을 따라 발생하는 회전을 정확히 반영하지 못한다.
- 좀 더 높은 수준의 결과물을 위해 회전의 움직임을 따르는 중간 사원수를 구하려면 두 사원수가 이루는 각을 Θ로 지정하고 주어진 비율 t를 사용해 두 각을 각각 tΘ와 (1 - t)Θ로 나눠야 한다.

- 위 그림을 만족시키는 선형 보간식의 두 계수 α와 β값을 찾아야 한다.
q' = α·q_1 + β·q_2
- 위 그림과 같이 첫 번째 사원수를 x축에 일치시키고 이를 회전한 값을 구해야한다.
첫 번째 사원수에 해당하는 벡터를 x, 두 번째 사원수에 해당하는 벡터를 u라고 할때
x에 직교하는 벡터를 y로, 구해야할 중간 사원수의 벡터를 v로 정하면
선형 보간식의 두 계수를 찾는 식은 다음과 같이 바꿔쓸 수 있다.
v = α·x + β·u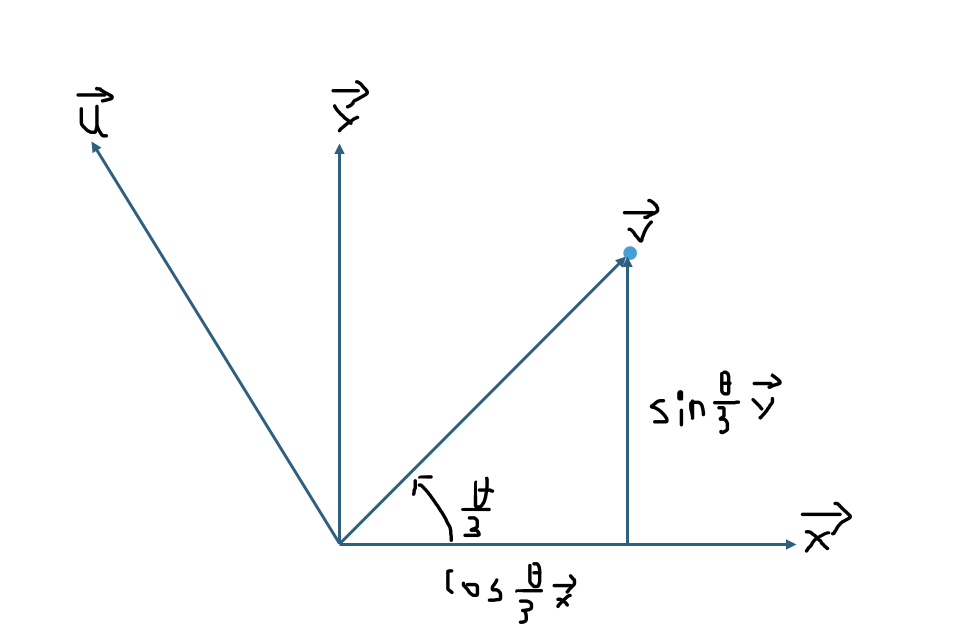
- 두 사원수가 만드는 각을 Θ라고 했을 때 구하려는 벡터 v는 서로 직교하는 두 기저벡터 x와 y의 조합으로 계산된다.
v = cos(tΘ)x + sin(tΘ)y- 하지만 벡터 x에 직교하는 벡터 y의 값을 모르므로 벡터 u와 삼각함수를 활용해 이를 구해야한다.
- 아래 그림을 보면 u - cosΘx값과 sinΘy값은 동일한 벡터를 가리킨다.
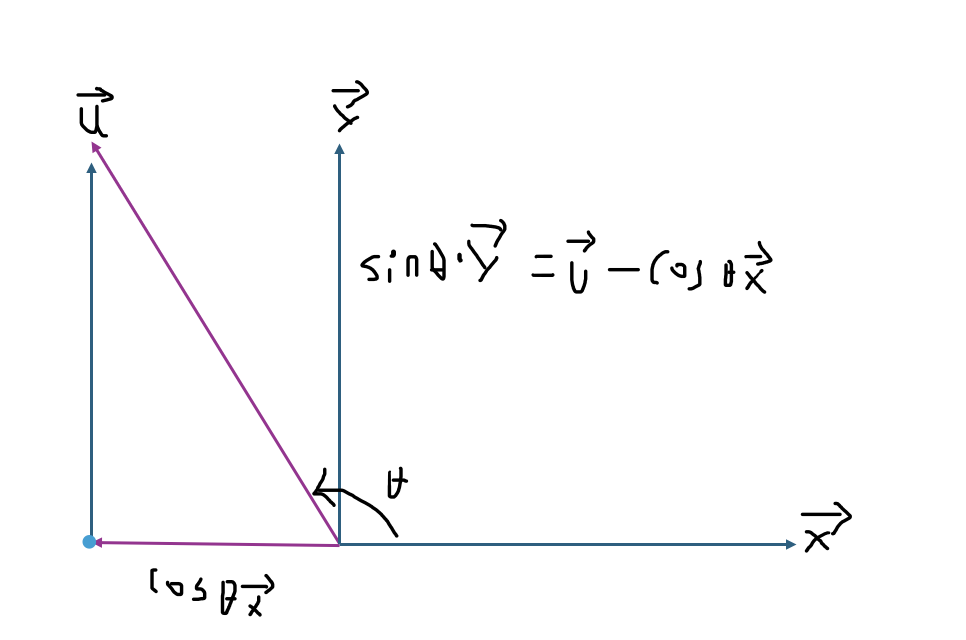
- 이를 활용하면 벡터 y의 값은 다음과 같이 구할 수 있다.
y = (u - cosΘx) / sinΘ- 이 값을 두 기저벡터의 조합을 통해 벡터 v를 구하는 식에 대입하면 다음과 같다.
v = cos(tΘ) + sin(tΘ)((u - cosΘx) / sinΘ)
= ((sinΘcos(tΘ) - cosΘsin(tΘ)) / sinΘ)x + (sin(tΘ)/sinΘ)u
= (sin(Θ - tΘ) / sinΘ)x + (sin(tΘ) / sinΘ)u- 위 식을 선형 보간식의 계수를 찾는 식을 벡터로 바꿔 쓴 식에 대입하면 두 계수를 구할 수 있다.
α = sin((1 - t)Θ) / sinΘ
β = sin(tΘ) / sinΘ- 계수를 중간 사원수를 구하는 식에 대입하면 구면으로 보간하는 최종 식이 만들어진다.
q' = (sin((1 - t)Θ) / sinΘ)·q_1 + (sin(tΘ) / sinΘ)·q_2- 이 방법으로 보간하는 방법을 구면 선형 보간(Spherical linear interplation)이라고 하며, 줄여서 슬럽(Slerp)이라 부른다.
- 구면 선형 보간을 구현하는데 필요한 두 계수의 식 외에 고려할 점이 몇가지 있다.
- 먼저 두 사원수로부터 나오는 회전 경로는 항상 긴 경로와 짧은 경로의 두 가지가 있는데, 이 중에 하나를 선택해야 한다는 점이 있다.
- 일반적으로 짧은 경로를 사용한다.
- 입력으로 들어온 두 사원수의 방향이 평행하면 분모 sinΘ의 값이 0이 되어 구면 선형 보간 계산이 불가능해진다.
- 따라서 긴 경로인지 파악하기 위해 이미 계산했던 내적을 활용해야 한다.
- 내적 값의 크기가 1이면 두 사원수는 평행한 상태이기 때문이다.
- 오차까지 감안해 두 사원수의 내적이 1과 매우 근접한 경우에는 일반 선형 보간을 사용해야 한다.
- 구면 선형 보간은 카메라의 움직임이나 캐릭터 에니메이션과 같이 시간에 따른 부드러운 회전을 구현하는데 유용하게 사용된다.
사원수의 활용
- 3차원 공간에서 움직이지 않는 물체의 회전을 설정하고, 회전에 관련된 정보를 보여줄 때는 오일러 각 방식을 사용하는 것이 편리하다.
- 단, 시간에 따라 변하는 회전을 처리할 때는 짐벌락 현상이 없는 사원수를 사용하는 것이 안전하고 간편하다.
- 따라서 3차원 트랜스폼을 안정적으로 구동시키기 위해서는 오일러 각 방식의 회전 시스템을 걷어내고 사원수 시스템을 사용해야한다.
- 하지만 오일러 각 방식은 회전을 지정하거나 게임 로직에서 사용하기 편리하기 때문에 사원수와 오일러 각이 자유롭게 변환되어야한다.
- 또한 렌더링 로직에는 회전 변환행렬이 필요하기 때문에 사원수로부터 행렬을 만드는 것도 사용해야 한다.
출처
https://m.yes24.com/Goods/Detail/107025224
이득우의 게임 수학 - 예스24
39가지 실시간 렌더링 게임 프로그래밍 실습 예제를 하나씩 따라 해보며 독자가 직접 체득하는 흥미로운 게임 수학의 세계! 게임 개발자와 그래픽 아티스트들이 궁금해 했던 3D 가상 세계와 메타
m.yes24.com
'게임수학' 카테고리의 다른 글
| [게임수학] 캐릭터 구축 (0) | 2024.05.08 |
|---|---|
| [게임수학] 극한과 오일러 공식 (1) | 2024.05.03 |
| [게임수학] 복소수 (1) | 2024.05.03 |
| [게임수학] 모델링과 뷰 (0) | 2024.04.28 |
| [게임수학] 절두체(Frustum) (0) | 2024.04.25 |
