원근 투영?
- 3차원 좌표 형태의 점을 스크린 위의 2차원 좌표로 투영하는 법
- 세상에는 많은 투영법이 존재한다.
원근 투영 변환
- 투시 원근법(Perspective projection) : 눈에 보이는 상을 그대로 화폭에 담기 위해 시선을 한 점에 고정시키고, 고정된 점으로부터 화폭까지 곧게 뻗은 실을 활용한 화법이며 르네상스 시대에 창안된 기법

- 우리 눈이 바라보는 방식으로 가상 공간을 변환하는 것을 원근 투영 변환(Perspective projection transformation)이라고 한다.
- 가상 공간에서 눈에 대응하는 물체는 카메라다.
- 원근 투영 변환을 설계하기 위해서는 눈에 보이는 범위를 카메라에도 설정해야 하는데 이를 화각(Field of view)라고 한다.
- 카메라에 화각을 설정하면 위 그림과 같이 좌우와 위아래가 균등한 사각뿔 영역이 만들어진다.
- 원근 투영 변환은 x, y, z축이 모두 직교하는 정육면체 형태를 가진 뷰 공간을 카메라의 한 점으로 모이는 사각뿔 형태를 가진 가상 공간으로 변환하는 작업이라고 할 수 있다.
- 3차원 공간을 변환한 후 공간의 물체를 투영해 2차원의 모니터 평면에 담아내야 한다.
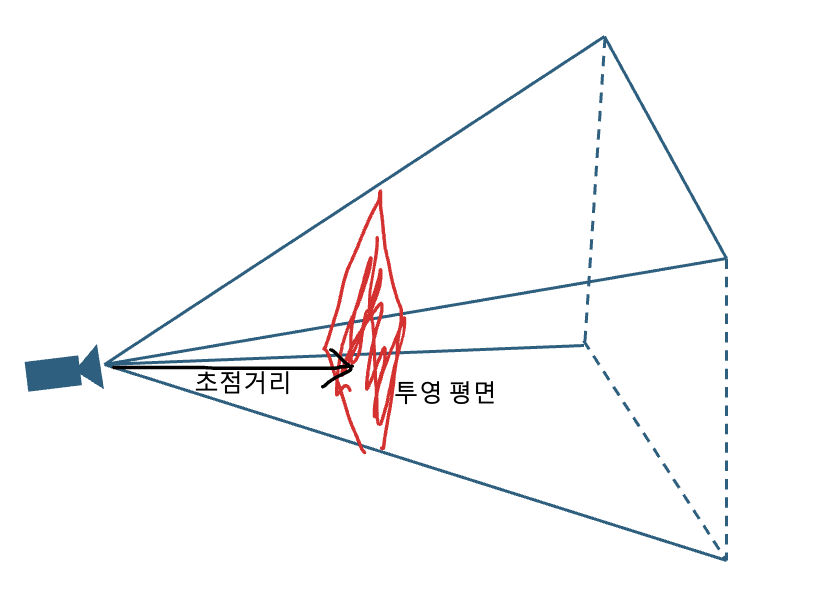
- 이를 위해 모든 물체의 상이 맺히는 가상의 평면을 생성해야 하는데, 이를 투영 평면(Projection plane)이라고 부른다.
- 투영 평면의 개념은 위 그림과 같으며 투영 평면의 위치가 카메라로부터 멀어질수록 투영 평면은 더 커진다.
- 투영 평면의 위치를 지정하기 위해 설정한 카메라로부터 투영 평면까지의 거리를 초점 거리(Focal length)라고 한다.

- 원근 투영을 구현하기 위해서는 투영 평면의 위치를 지정해야 한다.
- 일반적으로 투영 평면의 위치는 계산의 편의를 위해 위 아래의 크기가 각각 1이 되는 지점으로 결정한다.
- 좌우와 상하의 화각이 동일하므로 투영 평면은 위 그림과 같이 좌우와 상하가 각각 [-1, 1]의 범위를 가지는 정사각형의 모습을 띠며 이 평면에 물체의 상이 맺힌다.
- 투영 평면에 대응하는 정사각형 영역은 2차원 평면의 좌표시스템을 가지는데 이를 NDC(Normalized device coordinate)라고 부른다.
- NDC는 가운데 중점을 원점으로 설정한다.

- 투영 평면에 대응하는 NDC가 언제나 일정한 값을 가져야 한다면, 카메라에 설정된 화각이 변할때, 초점 거리는 달라질 수 밖에 없다.
- 화각이 커질수록 초점 거리는 가까워지고 화각이 작아질수록 초점 거리는 멀어진다.
- 화각과 초점 거리의 관계는 직각삼각형의 tan 함수로 설정된다.
tan(2/θ) = 1/d- 따라서 주어진 화각 θ에 따른 초점 거리 d는 다음 식으로 계산할 수 있다.
d = 1 / tan(2/θ)- tan 함수를 사용해 초점 거리를 구했다면, 뷰 공간의 점을 투영 평면 위의 점으로 대응시키는 원근 투영 변환을 설계해야 한다.
- 이 역시 행렬로 설계할 수 있다면 행렬 곱의 장점을 활용해 로컬 공간의 점을 투영 평면의 점으로 한 번에 변환해주는 파이프라인을 만들 수 있다.
- 지금까지 진행한 공간 변환은 모두 x, y, z축이 서로 직교하고 크기가 동일한 정육면체 형태의 3차원 공간이었다.
- 이렇게 세 축이 모두 직교하는 공간을 유클리드 공간(Euclidean space)이라고 한다.
- 로컬 공간, 월드 공간, 뷰 공간은 모두 유클리드 공간의 형태다.
- 그런데 정육면체 형태의 유클리드 공간은 원근 투영 변환에 의해 사각뿔 형태로 바뀌게 되었다.
- 이를 사영 공간(Projective space)이라고 한다.
- 사영 공간의 x축과 y축은 여전히 직교하기 때문에 사영 공간의 x축과 y축은 유클리드 공간과 같은 성질을 가진다.
- 하지만 사영 공간의 z축은 독립적으로 행동하지 않고 x축과 y축에 모두 영향을 준다.
- 이는 초점 거리에 따라 x축과 y축이 만들어내는 투영 평면의 면적이 달라지는 이유이기도 하다.
- 원근 투영 변환에 대응하는 행렬을 설계하기 위해서는 사영 공간이 지니는 특징을 파악해 행렬의 각 구성 요소를 펴즐 다루듯이 하나씩 풀어 나가야 한다.
- 유클리드 공간이 사영 공간으로 변환되면서 x, y, z축이 모두 직교하는 체계가 달라지기 때문에 원근 투영 변환에 대응하는 행렬은 지금까지 사용한 표준기저벡터의 변화를 관찰하는 방법으로는 생성할 수 없다.
- 문제를 단순화시키기 위해 x축을 배제한 y축과 z축으로 공간을 설정하고 투영 평면에 상이 맺히는 과정을 생각하면, 뷰 공간의 점 P_view가 투영 평면에 투영된 점을 P_ndc라고 할 때 투영 과정은 아래 그림과 같이 진행될 것이다.

- 뷰 공간의 점 P_view로부터 투영된 점 P_ndc의 좌표를 구해야 한다.
- x값을 0으로 고정한 상태이므로 둘의 좌표는 다음과 같다.
P_view = (0, vy, vz)
P_ndc = (0, ny)
- 두 점의 관계를 파악하기 위해 위 그림과 같이 닮은꼴 삼각형 두 개를 그렸다.
- 뷰 공간에서 카메라 앞에 위치한 점 z 값은 항상 음수이므로 큰 삼각형의 밑변의 길이는 -v_z가 된다.
- 두 삼각형의 닮은꼴 성질로부터 다음 비가 성립한다.
n_y : d = v_y : -v_z- 투영 평면의 y값 n_y는 다음 식으로 얻을 수 있다.
n_y = (d · v_y) / -v_z- 카메라 좌우와 상하의 사야각은 동일하므로 NDC의 x값 또한 y값을 0으로 고정한 후 x축과 z축의 평면을 사용하는 방식으로 구할 수 있다.
n_x = (d · v_x) / -v_z- 초점 거리와 뷰 좌표로부터 P_ndc는 다음과 같이 구할 수 있다.
P_ndc = (n_x, n_y)
= ((d · v_x) / -v_z, (d · v_y) / -v_z)
= -d/v_z(v_x, v_y)- NDC 좌표를 계산했다면 모니터의 최종 화면을 구성하는 작업이 필요하다.
- NDC 좌표를 화면 해상도만큼 가로와 세로를 늘려주면 최종 스크린 좌표가 완성된다.
- 하지만 단순히 늘리는 작업만 진행하면 물체가 찌그러지는 문제가 발생한다.
- 대부분의 경우 최종 화면의 크기 비율이 1:1로 균등하지 않기 때문이다.
- 문제의 원인이 되는 화면의 가로 세로 비를 종횡비(Aspect ratio)라고 한다.
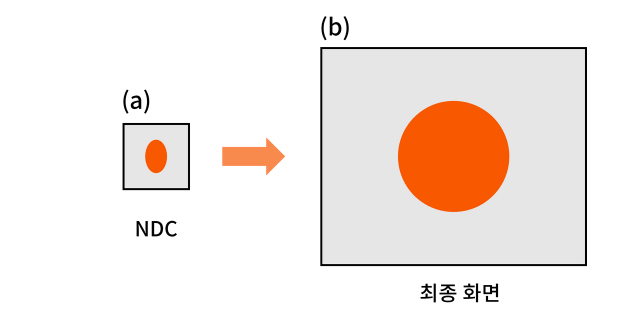
- 최종 화면을 구성하기 위해 화면의 종횡비를 미리 파악해 NDC 영역에서 미리 찌그러뜨린 후에 펼쳐야 한다.
- 위 그림의 (a)와 같이 NDC에 원을 투영할 때 종횡비를 거꾸로 뒤집은 비율을 적용해 먼저 찌그러트린다.
- 그러면 (b)와 같이 사용자 화면에 펼칠 때 원이 올바르게 보인다.
- 종횡비는 보통 하나의 축을 1의 크기로 지정하고 다른 축의 크기를 상대적으로 측정해 나타낸다.
- 800 x 600 해상도를 사용할 때 세로 기준으로 측정한 종횡비는 1.3333이 된다.
- 종횡비 기호는 a로 표시한다.
- 좌우로 찌르러트리려면 x축 값을 변경해야 한다.
- 이는 종횡비의 역수 1/a를 곱하면 된다.
- NDC whkvy P_ndc를 계산하는 공식은 다음과 같이 수정된다.
P_ndc = -d/v_z(v_x/a, v_y)- 최종 NDC 값을 계산하는 원근 투영 행렬 P는 다음과 같이 설계할 수 있다.
- 뷰 공간의 점 P_view의 x값과 y값으로 만든 벡터 v = (v_x, v_y)로 지정하면 P_ndc의 두 점의 좌표는 다음과 같이 계산할 수 있다.
P_ndc = P·v = ┌ 1/a·d/-v_z 0 ┐ · ┌ v_x ┐
└ 0 d/-v_z ┘ └ v_y ┘- 이렇게 만들어진 원근 투영 행렬을 사용할 때, 변환할 점의 z값이 행렬에 사용되다 보니 변환할 점마다 항상 행렬을 새롭게 생성해야 한다는 문제가 있다.
- 원근 투영 행렬에 변환할 점의 값이 사용되는 행렬을 사용하는 장점이 사라지고 만다.
- 따라서 원근 투영 행렬을 구성할 때 점의 값을 사용하지 않고 카메라 설정만으로 행렬을 만들 수 있어야 한다.
- 유도했던 투영 행렬을 살펴보면, 행렬의 요소는 모두 -v_z 값을 분모로 한다.
- 행렬에서 -v_z 값을 제거하고, 대신 행렬의 결과값에서 -v_z를 나누어주면 원하는 행렬을 만들 수 있다.
- 그러기 위해 NDC값을 만들어내는 과정을 두 단계로 분리해 봐야한다.
- 앞서 설게한 원근 투영 행렬 P를 다음과 같이 변경하고 행렬에 곱하는 벡터의 값을 v = (v_x, v_y, v_z)로 지정한다.
- 벡터 v는 뷰 좌표계의 점과 동일한 값을 가진다.
┌ d/a 0 0 ┐ ┌ v_x ┐ ┌ d/a·v_x ┐
P·v = | 0 d 0 | | v_y | = | d·v_y |
└ 0 0 -1 ┘ └ v_z ┘ └ -v_z ┘- 이 행렬 곱에서 생성된 벡터는 NDC 좌표와는 다르지만 원근 투영 행렬 P는 점과 무관하게 카메라 설정 값으로만 구성된다.
- 그렇다면 모든 점에 대해서 보편적으로 설계된 원근 투영 행렬 P를 사용할 수 있을 것이다.
- 이렇게 원근 투영 행렬 P로 변환되는 좌표계를 클립 좌표계(Clip coordinate)라고 부른다.
- 클립 좌표의 점 P_clip은 다음과 같이 계산된다.
P_clip = ((d·v_x) / a, d·v_y, -v_z)- 마지막 단계로 클립 좌표의 점 P_clip의 각 요소를 P_clip의 세 번째 값인 -v_z로 나누면 NDC의 좌표를 얻을 수 있다.
P_ndc = ((d·v_x) / (-v_z·a), (d·v_y) / -v_z, 1)동차 좌표계
- 동차는 모든 항의 차수가 같음을 의미하는 수학 용어다.
- 현재 차원에서 해결할 수 없는 문제를 더 높은 차원에서 해결할 수 있게 유도할 수 있다.
- 한 차원 높인 벡터를 사용하는 것을 게임 제작에서는 보통 동차 좌표계(Homogenous coordinate system)를 사용한다고 한다.
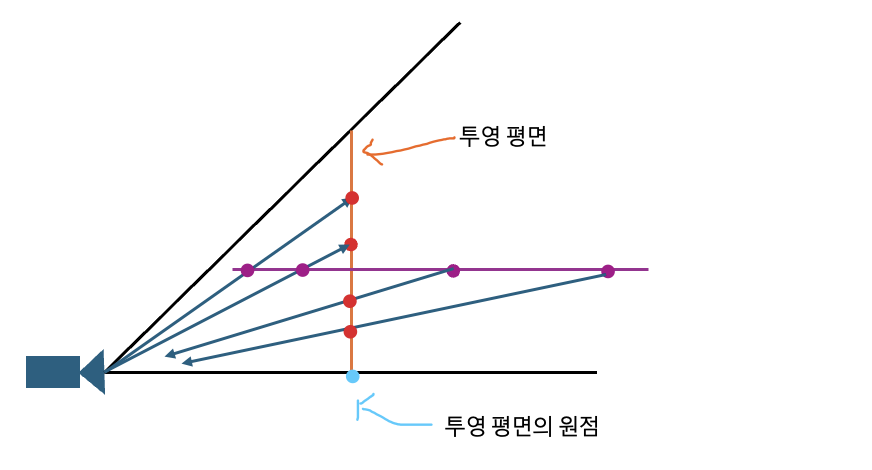
- 위 그림을 통해 3차원 사영 공간에서 평행하게 점을 이동시키면서 평면에 투영된 좌표 값이 어떻게 편하는지 알 수 있다.
- 사영 공간의 점과 투영된 점의 좌표는 카메라로부터 멀어질수록 원점에 가까워지고, 가까워질수록 커지는 반비례 관계를 가진다.
- 3차원 사영 공간의 점을 (x', y', z')으로 표기하고 해당 점이 투영된 NDC 좌표를 (x, y)로 표기해보면
- NDC 좌표값은 사영 공간의 마지막 차원 값 z'에 반비례로 영향을 받으므로 다음과 같은 관계가 성립할 것이다.
x = x'/z'
y = y'/z'- 직선의 방정식을 사영 공간의 좌표로 표현하면 다음과 같다.
y = ax + b에 동차를 적용
y'/z' = a(x'/z') + b
y'만 남기면 다음과 같다.
y' = ax' + bz'- 미지수에 대한 차수가 모두 동일한 방정식을 동차 방정식이라 부르며, 사영 공간이 사용하는 좌표계를 동차 좌표계라고 부른다.
- 원근 투영 변환에서 등장한 사영 공간, 클립 공간, 동차 공간은 모두 동일한 공간을 가리킨다.
- 클립 좌표, 동차 좌표도 동일한 좌표계를 카리킨다.
- 사영 공간의 점이 카메라로부터 멀어질수록 투영된 NDC 좌표값은 원점(0,0)에 가까워진다.
- 이는 회화의 투시 원근 기법에서 이야기하는 소실점(Vanishing point)에 해당한다.
소실점
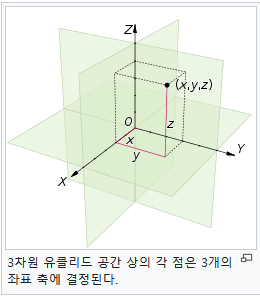
- 유클리드 공간 상의 3개의 축은 서로 직교하여 각 차원을 표현한다.
- 이 설명은 기하학적 설명으로 볼 수 있다.
- 수학적인 설명으로 유클리드 좌표를 설명해보라고 하자면 각 축들이 서로 영향을 주지 않는다.
- 즉, 각 축들에 대한 내적값이 0이 되는 것을 의미한다고 볼 수 있다.

- 소실점이 있는 사각뿔 형태의 원근 투영 공간은 는 직교하되 는 직교하지 않는 공간이다.
- 따라서 축의 위치에 따라 의 변형이 일어나는 것이라고 수학적 설명이 가능
- 소실점은 투영 평면과 카메라 사이의 거리가 무한대로 길어진다면
- 결국 투영 평면의 가로와 세로는 0에 수렴하게 된다고 설명을 할 수 있다.
초점거리인 d를 무한대로 적용하면 투영 화면인 P는?
P -> (0, 0, 1)에 수렴깊이?
- 깊이(Depth)는 카메라로부터 물체가 얼마나 떨어졌는지 파악할 수 있는 데이터이다.
- 화면은 2차원 평면이므로 나중에 그린 물체가 앞에 보일 수 밖에 없다.
- 화면에 크게 그린 물체는 카메라에서 가장 가깝지만, 가장 마지막에 그리면 가장 먼 곳에 배치된 것처럼 느낀다.
- 이 문제를 해결하기 위해 물체가 카메라로부터 얼마나 떨어져 있는지에 대한 정보를 기록해 앞에 있는 물체를 가장 마지막에 그리도록 설정해야 한다.
- 픽셀의 깊이는 0.0 ~ 1.0 사이의 값을 가진다.
- 0.0은 카메라와 가장 가까운 픽셀에 해당
- 1.0은 가장 먼 픽셀에 해당

- 2차원 평면이었던 NDC 영역에 깊이 값을 추가하면 위 그림과 같은 3차원으로 NDC 영역에 확장된다.
- 카메라에 부여한 시야각은 깊이와 무관하기 때문에 카메라에 추가 속성을 부여해야 한다.
- 이를 각각 근평면(Near plane)과 원평면(Far plane)이라는 속성이 추가된다.

- 카메라 시야를 구성하는 사영 공간을 근평면과 원평면으로 잘라주면 사각뿔에서 뿔부분이 잘린 형태가 나오는데 이를 절두체(Frustum)라고 한다.

- 절두체로 생성되는 3차원 NDC 영역의 범위는 위 그림과 같이 구성된다.
- NDC의 깊이 값은 멀어질수록 증가하기 때문에 3차원 NDC 공간은 왼손 좌표계를 형성한다.
- 원근 투영 행렬을 다른 행렬과의 곱을 위해 3x3 크기의 행렬을 인위적으로 4x4크기로 늘리면 다음과 같다.
┌ d/a 0 0 0 ┐
P = │ 0 d 0 0 │
│ 0 0 -1 0 │
└ 0 0 0 1 ┘- 원근 투영 행렬의 3행을 4행으로 옮기고 3행을 깊이 값을 구하는 용도로 변경한다.
- 뷰 공간의 점을 나타내는 v의 값을 (v_x, v_y, v_z, 1)로 지정하면 원근 투영 행렬 P는 다음과 같이 구성된다.
┌ d/a 0 0 0 ┐┌ v_x ┐ ┌ d/a·v_x ┐
P·v = │ 0 d 0 0 ││ v_y │ = │ d·v_y │
│ i j k l ││ v_z │ │ ? │
└ 0 0 -1 0 ┘└ 1 ┘ └ -v_z ┘- 깊이 값을 계산하는데 사용하는 3행은 네 개의 미지수로 지정할 수 있다.
- 깊이 값은 뷰 좌표계의 x축과 y축에 각각 직교하므로 영향을 받지 않는다.
- 앞의 두 요소 i와 j 값은 0으로 설정해야 한다.
- 3행에는 두 개의 미지수 k와 l만 남게된다.
- 두 미지수를 얻기 위해선 카메라에 설정된 근평면과 원평면의 값을 사용하면 된다.
- 카메라로부터 근평면까지의 거리를 n, 원평면까지의 거리를 f로 설정
- 뷰 공간에서 카메라 시선 방향은 -z축이므로 뷰 공간에서 카메라의 중심으로부터 시선 방향으로 n만큼 이동한 근평면 상의 점의 좌표는 (0, 0, -n, 1)이 된다.
- 이 좌표는 깊이 값의 시작 지점이기 때문에 NDC 좌표 (0, 0 , -1)에 대응한다.
- 뷰 공간의 원 평면상의 좌표는 (0, 0, -f, 1)인데, 이는 깊이 값의 끝지점이기 때문에 NDC 좌표 (0, 0, 1)에 대응한다.
- 원근 투영 행렬에 뷰 공간의 점을 곱한 결과는 클립 좌표가 된다. 근 평면의 점을 P_1, 원 평면의 점을 P_2라고 하면, 다음과 같이 계산된다.
┌ d/a 0 0 0 ┐┌ 0 ┐ ┌ 0 ┐
P_1 = │ 0 d 0 0 ││ 0 │ = │ 0 │
│ 0 0 k l ││ -n │ │ ? │
└ 0 0 -1 0 ┘└ 1 ┘ └ n ┘
┌ d/a 0 0 0 ┐┌ 0 ┐ ┌ 0 ┐
P_2 = │ 0 d 0 0 ││ 0 │ = │ 0 │
│ 0 0 k l ││ -f │ │ ? │
└ 0 0 -1 0 ┘└ 1 ┘ └ f ┘- 아직 원근 투영 행렬의 k와 l을 모르기 때문에 클립 좌표의 세 번째 요소를 계산할 수 없다.
- 하지만 클립 좌표의 네 번째 요소로 모든 요소를 나눈 값은 NDC 좌표를 가리키고, NDC 좌표의 z값은 각각 -1과 1이다.
- 따라서 근평면의 클립 좌표는 (0, 0, -n, n)이 돠고, 원평면의 클립 좌표는 (0, 0, f, f)가 되어야 한다.
- 따라서 다음 식을 얻을 수 있다.
┌ d/a 0 0 0 ┐┌ 0 ┐ ┌ 0 ┐
P_1 = │ 0 d 0 0 ││ 0 │ = │ 0 │
│ 0 0 k l ││ -n │ │ -n │
└ 0 0 -1 0 ┘└ 1 ┘ └ n ┘
┌ d/a 0 0 0 ┐┌ 0 ┐ ┌ 0 ┐
P_2 = │ 0 d 0 0 ││ 0 │ = │ 0 │
│ 0 0 k l ││ -f │ │ f │
└ 0 0 -1 0 ┘└ 1 ┘ └ f ┘- 두 행렬의 3행과 뷰 공간의 점을 내적하면 다음 두 식을 얻을 수 있다.
-kn + l = -n
-kf + l = f- n과 f는 카메라에 설정된 상수이므로 두 식을 서로 빼 l을 소거한 후 k값을 구하면 다음과 같다.
k = -(n + f) / (-n + f) = (n + f) / (n - f)
k를 대입해 l을 계산한 결과
l = 2nf / (n - f)- 결과적으로 깊이 값까지 산출해주는 최종 원근 투영 행렬 P는 다음과 같다.
┌ d/a 0 0 0 ┐
P = │ 0 d 0 0 │
│ 0 0 (n+f)/(n-f) 2nf/(n-f) │
└ 0 0 -1 0 ┘원근 보정 매핑
- 정육면체에 텍스처를 입히기 위해 각 필셀에 무게중심좌표를 구하고, 이로부터 UV 값을 계산하고 이에 대응하는 텍스처의 색상을 가져와 텍스처 매핑을 구현하면, 의도한 텍스처와 다르게 그려질 때가 있다.
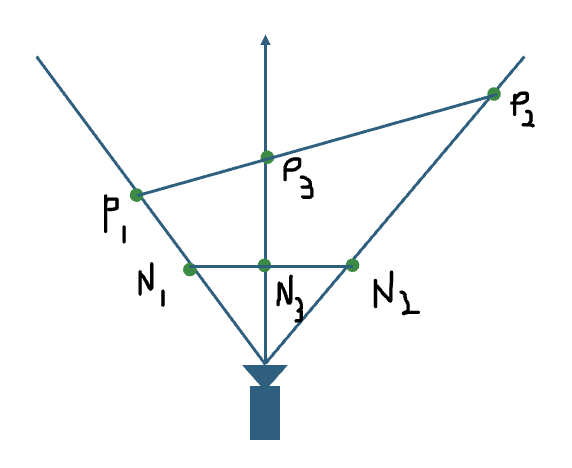
- 위 그림을 통해 투영 전과 투영 후의 과정을 살펴보면 다음과 같다.
- 투영하기 전 사영 공간의 두 점 P_1과 P_2가 카메라 시야각에 걸쳐 있다고 가정
- 두 점을 투영 평면에 투영한 점 N_1과 N_2의 NDC 좌표의 x값은 각각 -1과 1이 된다.
- 카메라 정면에 위치한 사영 공간의 점 P_3를 투영한 NDC 좌표의 점 N_3는 투영 평면의 정 중앙에 위치
- NDC공간에서 점 N_1과 N_2를 이어 선분을 생성했을 때 선분의 중앙에 위치한 중점 N_3의 무게중심좌표는 0.5가 된다.
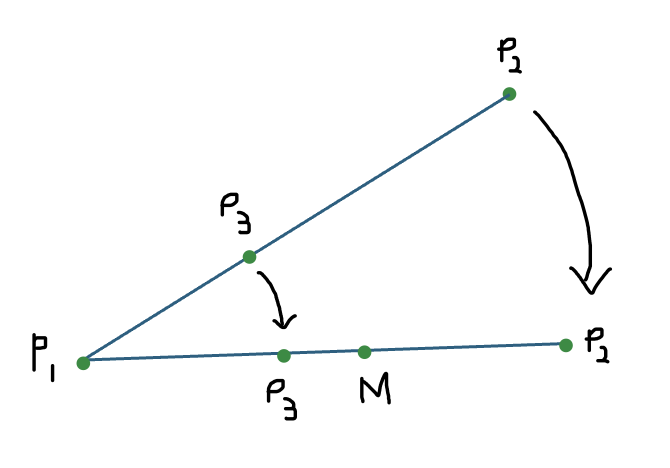
- 위 그림과 같이 투영 전 무게중심좌표를 생각해보면
- 사영 공간의 선분 P_1P_2 내에 위치한 점 P_3의 무게중심좌표는 0.5보다 작은 값임을 알 수 있다.
- 즉, 사영 공간의 무게중심좌표와 NDC에서의 무게중심좌표는 서로 다르다는 사실을 알 수 있다.
- 사영 공간의 무게중심좌표와 NDC에서의 무게중심좌표가 서로 차이 나는 이유는 NDC 공간으로의 변환 과정에서 사영 공간의 마지막 요소 w의 값 -v_z를 나눴기 때문이다.
- 이는 사영 공간과 NDC 공간 사이에 형성된 반비례 관계로부터 기인한다.
- 텍스처 매핑을 진행할때 NDC에서 변경된 무게중심좌표를 사용하지 않기 위해선, 투영되기 전 사영 공간에서의 무게중심좌표를 사용해야한다.
- 따라서 투영 과정을 거꾸로 추적해 NDC에서 구한 무게중심좌표로부터 사영 공간의 무게중심좌표를 계산해야 한다.
- 투영 전의 무게중심좌표 값을 계산해 텍스쳐를 매핑하기 위해 투영 보정 보간(Perspective correction interpolation)을 사용해야 한다.
- NDC의 무게중심좌표를 사영 공간의 무게중심좌표로 돌려주는 투영 보정 보간의 계산식을 유도하기 위해선 반비례 함수 y = -1/x가 가진 성질을 알아봐야 한다.

- y = -1/x 함수에서 x축에 위치한 세 수 2, 4, 6이 대응된 y값은 각각 -1/2, -1/4, -1/6이다.
- x축에 위치한 세 수중 가운데 위치한 4의 무게중심좌표 a는 다음 식에 의해 0.5가 된다.
4 = a·2 + (1-a)·6- 4에 대응하는 y값 -1/4의 무게중심좌표를 구하면 다음 식에 의해 해당 값의 무게중심좌표는 0.25가 된다.
-1/4 = a·(-1/2) + (1-a)·(-1/6)- 만일 y축의 무게중심좌표 0.25로 부터 x축의 무게중심좌표 0.5를 계산해주는 식을 찾을 수 있다면, 이를 응용해 사영 공간에서의 무게중심좌표를 계산할 수 있을 것이다.
- y축에서의 무게중심좌표를 q_1과 q_2로 지정하고 이를 사용해 y축의 두 점 y_1과 y_2 사이의 점 y'를 구하는 수식을 다음과 같이 정리해 볼 수 있다.
- 무게중심좌표의 정의에 의해 두 무게중심좌표의 합 q_1 + q_2의 값은 1이다.
y' = q_1·y_1 + q_2·y_2- 반비례가 적용되기 전 x축의 수식을 정리하면 다음과 같다.
- x축에서 무게중심좌표를 t_1과 t_2로 지정하고 이를 사용해 x축의 두 점 x_1과 x_2사이의 점 x'을 구하는 수식
x' = t_1·x_1 + t_2·x_2- 두 값 x'과 y'은 서로 반비례 관계이므로 y'의 식의 y값을 x값으로 표현하면 다음 식이 성립한다.
1/x' = q_1·(1/x_1) + q_2·(1/x_2)- 주어진 두 점 y_1과 y_2의 값과 둘의 무게중심좌표 q_1과 q_2를 사용해 x'값을 계산할 수 있다.
x' = 1 / (q_1·(1/x_1) + q_2·(1/x_2))
양변에 분모를 곱하면 다음 식이 성립
x'·(q_1·(1/x_1) + q_2·(1/x_2)) = 1
q_1·(x'/x_1) + q_2·(x'/x_2) = 1- 다음 과정을 거치면 최종 관계를 얻을 수 있다.
두 무게중심좌표의 합은 1임을 이용해 식을 변환
q1·(x'/x_1) + q2·(x'/x_2) = t_1 + t_2
양변의 덧셈항을 분리하면 다음 관계를 얻을 수 있다.
t_1 = (x'/x_1)·q1
t_2 = (x'/x_2)·q2- 위 식에서 얻은 관계를 통해 x축에서의 무게중심좌표 0.5가 잘 계산됨을 확인
q_1 = 1/4, q_2 = 3/4
t_1 = (x'/x_1)- 두 점의 조합에 대한 무게중심좌표를 확장해 삼각형을 구성하는 세 점의 조합에도 동일하게 적용할 수 있을 것
x' = 1/(q_1·(1/x_1) + q_2 ·(1/x_2) + q_3·(1/x_3))
t_1 = (x'/x_1)·q_1
t_2 = (x'/x_2)·q_2
t_3 = (x'/x_3)·q_3- 사영 공간에서 NDC로 변환할 때 나누는 값은 뷰 공간의 z값이므로, 위 식에서 x를 -z로 치환하면 최종 투영 보정 보간의 식을 얻을 수 있다.
z' = 1/(q_1·(1/z_1) + q_2 ·(1/z_2) + q_3·(1/z_3))
t_1 = (z'/z_1)·q_1
t_2 = (z'/z_2)·q_2
t_3 = (z'/z_3)·q_3- 원근 보정 매핑(Perspective correction mapping) : 투영 보정 보간의 수식을 활용해 카메라로부터 빗겨나간 평면의 텍스쳐가 찌그러진 현상을 잡아주는 것
깊이 버퍼
- 깊이는 깊이 버퍼(Depth Buffer)에 값이 매핑된다.
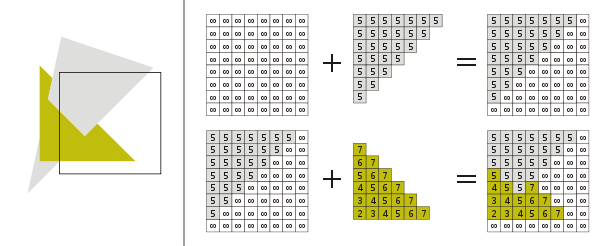
- 픽셀간에 가장 가까운 픽셀을 판단하는 것을 Z-버퍼링(Z-Buffering)이라고 한다.
- 이를 통해 어떤 오브젝트를 먼저 그릴지 고민하지 않아도 된다.
- 하나의 픽셀에 여러개의 물체가 겹쳐 있다면, Z-buffer에 저장된 z값과 새로 그려야할 물체의 z값을 비교해 더 작은 값을 렌더링하고, Z-buffer에 덮어 씌우는 방식
- 최종 픽셀을 찍는 과정에서 현재 깊이 값을 깊이 버퍼에 저장된 값과 비교해 현재 깊이 값이 작은 경우에만 픽셀을 찍고록 로직을 구현하면 그리기 순서 문제를 해결하면서 물체에 가려져 그려지지 않아도 되는 픽셀을 파악해 그리기를 건너띌 수 있다.
- 이 작업을 깊이 테스팅(Depth testing)이라고 한다.
출처
https://m.yes24.com/Goods/Detail/107025224
이득우의 게임 수학 - 예스24
39가지 실시간 렌더링 게임 프로그래밍 실습 예제를 하나씩 따라 해보며 독자가 직접 체득하는 흥미로운 게임 수학의 세계! 게임 개발자와 그래픽 아티스트들이 궁금해 했던 3D 가상 세계와 메타
m.yes24.com
https://wecandev.tistory.com/217
[이득우 게임수학] 12. 원근 투영: 화면에 현실감을 부여하는 변환
12.1 원근 투영 변환의 원리 투시 원근법(Perspective projection) : 눈에 보이는 상을 그대로 화폭에 담기 위해 시선을 한 점에 고정시키고, 고정된 점으로부터 화폭까지 곧게 뻗은 실을 활용한 화법이
wecandev.tistory.com
https://kkadalg.tistory.com/23
깊이 버퍼(Depth Buffer)
깊이 버퍼(Depth Buffer) 깊이 버퍼는 이미지가 굳이 필요 없는 텍스쳐이다. 왜냐하면 각 픽셀의 깊이 정보만 담으면 되기 때문이다. 픽셀의 깊이는 0.0 ~ 1.0 사이의 값으로 지정되는데, 0.0은 관찰자(
kkadalg.tistory.com
https://velog.io/@ounols/%EA%B2%8C%EC%9E%84-%EC%88%98%ED%95%99-%EC%9B%90%EA%B7%BC-%ED%88%AC%EC%98%81
[게임 수학] 원근 투영
🧐 해당 파트는 게임 개발 환경을 구성하는 컴퓨터 그래픽스(Computer Graphics)를 이해하기 위한 기초 수학의 간단한 개념에 대해 설명하고 있습니다!혹여나 이해가 잘 안되거나 잘못된 정보를 발
velog.io
'게임수학' 카테고리의 다른 글
| [게임수학] 모델링과 뷰 (0) | 2024.04.28 |
|---|---|
| [게임수학] 절두체(Frustum) (1) | 2024.04.25 |
| [게임수학] 벡터의 외적 (0) | 2024.04.23 |
| [게임수학] 3차원 공간 (0) | 2024.04.23 |
| [게임수학] 정점과 삼각형 (1) | 2024.04.23 |
