공간 이동
- 3차원 공간의 이동 구현을 위해선 물체를 표현하는 3차원 + 이동을 표현하는 1차원이 필요
- 총 4차원이 필요하다.
- 4차원 공간을 그림으로 표현할 수 없음
- 단, 2차원 공간의 이동은 그림으로 표현할 수 있음
- 2차원 공간의 이동은 3차원 공간에서 가능하다.

- 2차원 물체를 표현하기 위해서 사용하는 공간은 노란색 영역
- 노란색 영역의 마지막 차원의 값인 z는 항상 1이다.
- 이 노란색 영역의 이름을 어파인(Affine) 공간이라고 한다.
어파인 조합(Affine Combination)
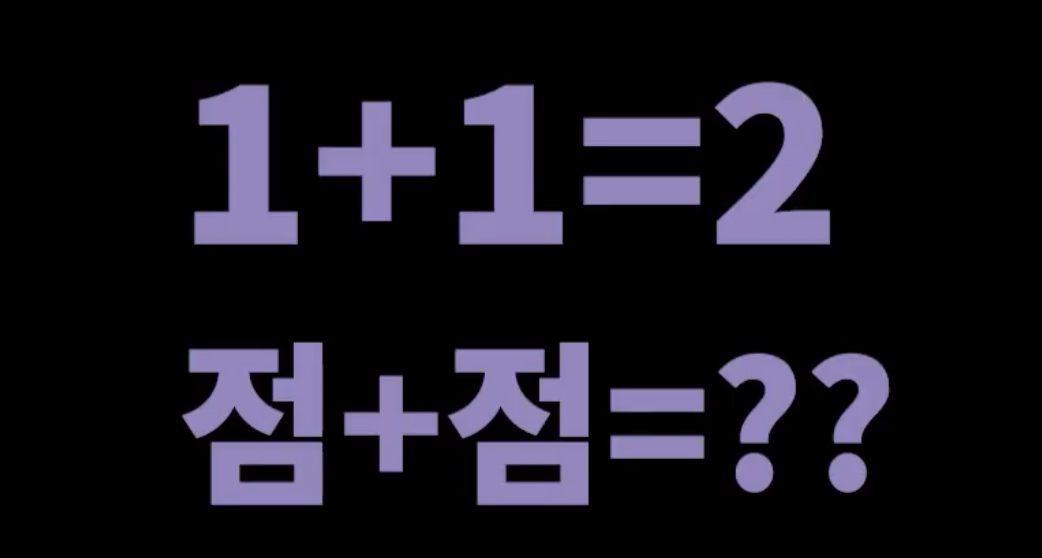
- 점 + 점 = 2이므로 어파인 공간의 영역을 벗어나게 된다.
- 따라서 점 + 점은 불가능
- 하지만 아래와 같이 점 앞에 계수를 붙이면
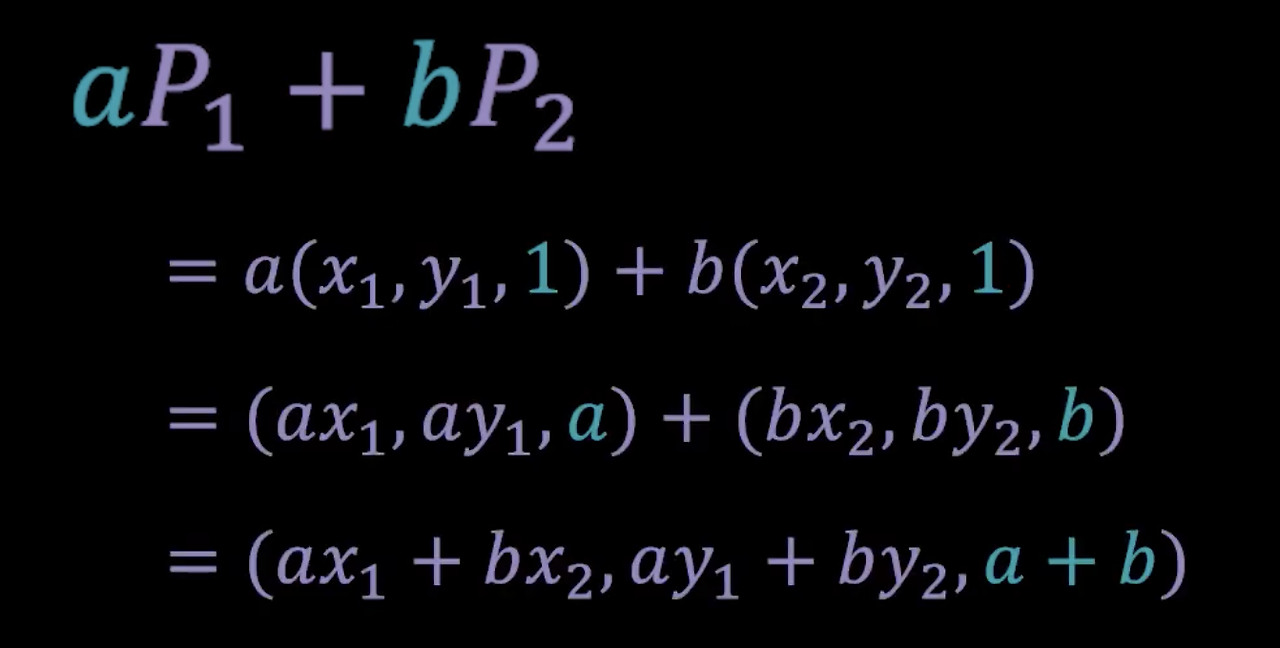
- 두 점을 더한 결과가 a + b가 된다.
- 만약, a + b의 결과가 1인 경우

- 두 점을 더했을 때 점이 되는것을 알 수 있다.
- a + b = 1일 때 b를 1 - a로 바꿀 수 있다.
- 이 경우 a의 값과 무관하게 두 점의 합은 항상 마지막 차원의 값인 1이 된다.
- 이 공식은 점과 점을 더했을 때 항상 어파인 공간의 점임을 보장한다.
- 점과 점을 조합하여 새로운 점을 생성하는 공식으로 사용된다.
- 이러한 공식을 게임수학에서는 어파인 조합이라고 한다.
- 어파인 조합은 물체를 구성하는데 기본이 되는 중요한 공식
세 점의 결합
- 세점 P1, P2, P3 를 결합하는 경우 스칼라는 2개에서 3개로 늘어나는데 세 스칼라의 합은 1이 되어야 한다.
- 따라서 어파인 결합식은 아래와 같이 전개 된다.
P` = s·P1 + t·P2 + (1-s-t)·P3
(P` - P3) = s(P1 - P3) + t(P2 - P3)
//w = (P` - P3)
//u = (P1 - P3)
//v = (P2 - P3) 치환
w = s·u + t+v- 벡터 u와 v가 서로 선형 독립의 관계라면 벡터 w는 2차원 벡터 공간 R^2에 존재하는 모든 벡터를 생성할 수 있다.
- 세 점의 어파인 결합은 평면의 모든 점을 만들어낸다.

- 선분을 만들어지는 조건과 동일하게 s와 t의 값을 [0, 1] 범위로 고정시키면
- 위 그림과 같이 스칼라 s와 t 값을 몇 가지로 지정해보면 해당 영역은 삼각형이 됨을 알 수 있다.
- 어파인 결합식에서 스칼라 값을 [0, 1] 범위로 제한하면 시작과 끝의 범위과 명확해지므로 선분과 동일하게 그릴 수 있는 도형이 만들어진다.
- 범위를 제한한 결합을 컨벡스 결합(Convex Combination)이라고 한다.
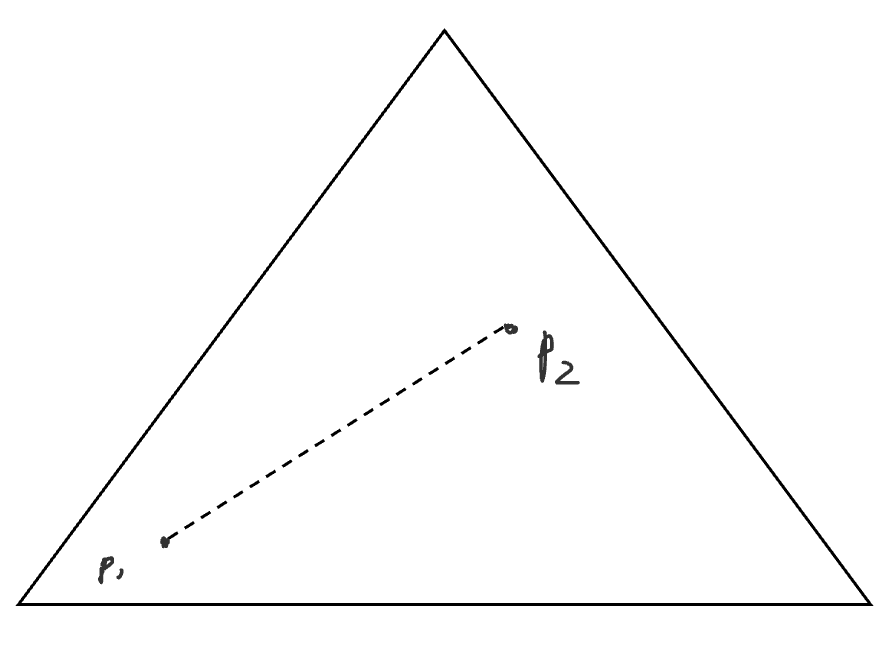
- 선분이나 삼각형처럼 컨벡스 결합으로 만든 영역을 컨벡스 영역(Convex region)이라고 한다.
- 컨벡스 영역이란 볼록한 형태의 영역이라 해석할 수 있다.
- 수학에서 정의한 볼록함이란, 영역 내 임의의 두 점을 연결한 선분을 만들었을 때 그 선분은 언제나 해당 컨벡스 영역 안에 속하는 성질을 의미한다.
- 삼각형 내 임의의 두 점 P1과 P2를 선택해 선분을 그리면, 선분은 언제나 삼각형 내에 속한다.
- 컨벡스의 반대는 오목한 모양을 뜻하는 컨케이브(Concave)다.
- 컨케이브의 영역은 임의의 두점을 이은 선분이 영역 밖으로 벗어나는 경우가 발생한다.
- 어파인 공간에서 점 4개를 결합한 식을 벡터로 바꿔 표현하면 다음과 같이 전개될 것이다.
x = a·u + b·v + c·w- 세 벡터 u, v, w가 선형 독립 관계를 이룬다면 3차원 공간의 모든 벡터를 생성할 수 있으므로 어파인 결합으로 생성된 벡터 x는 3차원 공간의 벡터가 될 것이다.
- 이때 스칼라 a, b, c의 값을 [0, 1] 범위로 제한한다면 아래 그림과 같은 삼각뿔 영역이 형성된다.
- 삼각뿔 영역 또한 내부의 두 점을 연결한 선분은 항상 해당 영역에 속하는 컨벡스 성질을 가진다.

- 컨벡스 결합으로 만들어지는 1차원의 선분, 2차원의 삼각형, 3차원의 삼각뿔 중에서 가상 공간의 물체를 표현하는데 가장 적합한 도형은 삼각형이다.
- 삼각형으로 2차원의 물체를 효과적으로 표현할 수 있으며, 3차원 물체도 표면만을 다루기 때문에 삼각형으로 표현하는게 효과적
- 점을 사용하지 않고 삼각형을 사용해서 물체를 표현하는 이유
- 점으로 물체를 표현하고 가까이서 물체를 보면 점들이 퍼지게 되어 물체를 제대로 볼 수가 없게 된다.
- 삼각형으로 물체가 가지는 영역을 설정한 다음에 삼각형 내부에 위치한 픽셀의 수를 구한다.
- 그 다음 픽셀을 칠하면 물체를 정밀하게 표현할 수 있다.
메시(Mesh)
- 3차원 공간의 입체적인 물체 또한 삼각형을 이어붙이면 표현이 가능함
- 물체를 표현하기 위해 삼각형의 데이터를 체계적으로 읽고 쓰는 방법이 필요함
- 삼각형을 중심으로 물체에 관련된 정보를 기록한 데이터를 메시(Mesh)라고 한다.
- 메시는 다수의 삼각형으로 구성되고, 메시를 이루는 삼각형은 다시 3개의 점으로 구성된다.
- 정리하면 메시는 다수의 점으로 구성된다고 말할 수 있다.
- 메시는 삼각형을 통해 물체의 외형을 표현하기 때문에, 삼각형을 이루는 각 점의 위치를 가지고 있어야 한다.
- 위치 정보만 담지 않고, 물체를 표현하는데 활용할 수 있는 색상이나 방향과 같은 부가 정보도 담아 함께 제공
- 위치 정보와 부가 정보를 묶은 특별한 점을 정점(Vertex)라고 한다.
- 메시는 정점들이 모인 데이터라고 할 수 있다.
- 컴퓨터에서 메시를 읽어 물체를 표현할 때는 메시의 정점 정보를 빠르게 읽기 위해서 메모리에 정점 정보를 일렬로 나열하는 배열의 형태로 관리함
- 이를 정점 버퍼(Vertex buffer)라고 한다.
- 하지만 정점 버퍼의 정보만으로는 어떤 세 정점이 모여 삼각형을 구성하는지 알 수 없다.
- 삼각형을 구성하는 정점의 인덱스만 기록한 배열을 별도로 만들어 관리함
- 이를 인덱스 버퍼(Index buffer)라고 한다.
- 인덱스 정보는 삼각형의 수만큼 필요하기 때문에 인덱스 버퍼의 크기는 항상 3의 배수다.
- 정점 버퍼와 인덱스 버퍼의 두 가지 배열 정보를 사용해 삼각형들을 하나씩 그려나가면 최종적으로 물체를 표현할 수 있다.
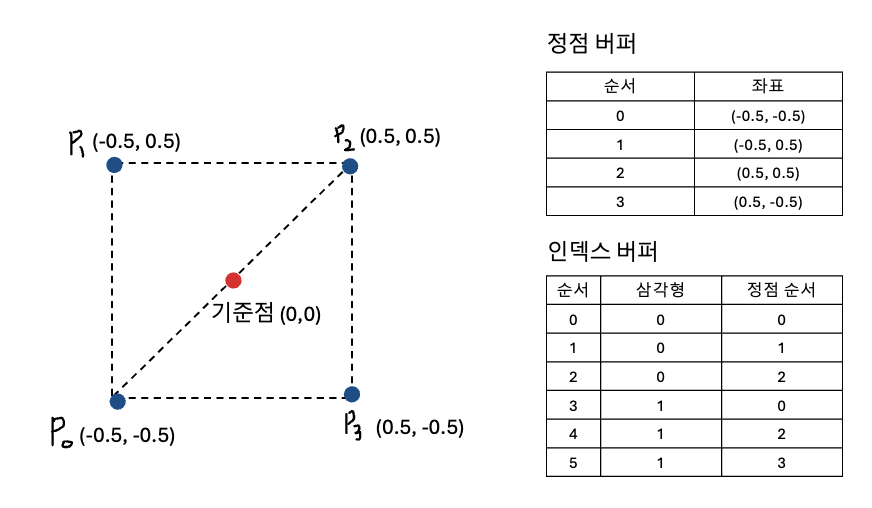
- 위 그림은 두 개의 삼각형으로 이루어진 정사각형 메시를 정점 버퍼와 인덱스 버퍼로 저장한 것이다.
- 두 삼각형이 빗변을 맞대고 나란히 붙어있다면 0번째 점과 2번째 점은 두 삼각형이 공유해 사용할 수 있다.
- 정점 배열과 인덱스 배열을 채운 후, 삼각형을 구성하는 세 점에서 두 점씩 묶어 선으로 삼각형을 표현해나가면 메시를 형상화 할 수 있다.
- 삼각형의 외각선만 그려 메시를 표현하는 방법을 와이어프레임(Wireframe)이라고 한다.
무게중심좌표
P` = s·P1 + t·P2 + (1-s-t)·P3- 위 식에서 사용된 세 스칼라 s, t, 1-s-t는 모두 실수이므로, 이들을 묶어서 하나의 3차원 벡터를 생성할 수 있다.
- 이렇게 어파인 결합의 스칼라를 묶어 만든 좌표를 무게중심좌표(Barycentric coordinate)라고 한다.
- 무게중심좌표는 아래 그림과 같이 삼각형에 대한 정보를 담고 있기에, 삼각형에 관련된 기능을 구현할 때 유용하게 활용된다.
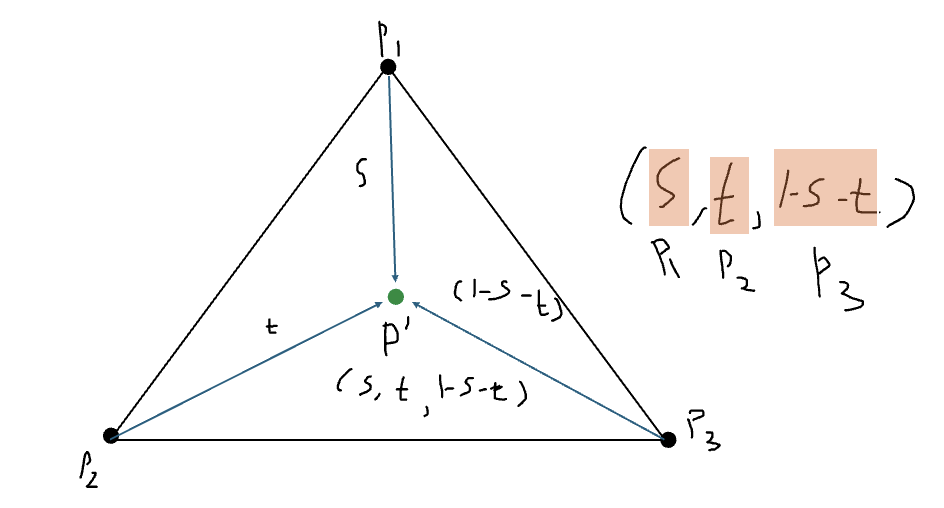
무게중심좌표의 계산
- 세 점의 어파인 결합이 삼각형이 되려면 모든 스칼라의 값이 [0, 1] 범위 내에 있어야 했다.
- 무게중심좌표를 구성하는 스칼라 값이 하나라도 [0, 1] 범위를 벗어난다면 어파인 결합으로 생성된 점은 삼각형 외부에 있다고 할 수 있다.
- 이러한 성질을 활용하면 주어진 점이 삼각형 영역의 내부에 있는지 외부에 있는지 판단할 수 있다.

- 세 점의 어파인 결합 수식을 벡터로 변경한 식인 w = s·u + t+v를 도식화하면 위 그림과 같다.
- 여기서 어파인 결합으로 생성되는 점 P'가 삼각형 내부에 있는지 판별하기 위해 다음과 같은 수식을 사용한다.
// P3 -> P1 = u
// P3 -> P2 = v
// P3 -> P` = w (P`= 무게중심좌표)
w·u = (s·u + t·v) · u
w·v = (s·u + t·v) · v
//분배법칙
w·u = s(u·u) + t(u·v)
w·v = s(u·v) + t(v·v)
//s 소거를 위해 다음과 같이 전개
(w·u)(u·v) = s(u·u)(u·v) + t(u·v)(u·v)
(w·v)(u·u) = s(u·v)(u·u) + t(v·v)(u·u)
//위 식에서 아래식을 빼 s를 소거하고 t만 남김
t = ((w·v)(u·v) - (w·v)(u·u)) / ((u·v)^2 - (u·u)(v·v))
//t 소거를 위해 다음과 같이 전개
(w·u)(v·v) = s(u·u)(v·v) + t(u·v)(v·v)
(w·v)(u·v) = s(u·v)(u·v) + t(v·v)(u·v)
//위 식에서 아래식을 뺴 t를 소거하고 s만 남김
s = ((w·v)(u·v) - (w·v)(v·v)) / ((u·v)^2 - (u·u)(v·v))- 이렇게 얻어진 무게중심좌표 (s, t, 1-s-t)의 세 값 모두 [0, 1] 범위 안에 있다면 점 P4는 삼각형 안에 있다고 판별할 수 있다.
- 벡터 u 또는 v의 크기가 0이거나 두 벡터가 이루는 각이 0도 이거나 180도 인 경우
- 두 벡터는 평행한 상태임을 의미한다.
- 두 벡터가 평행하면 선형 종속의 관계를 이룬다.
- 선형 종속의 관계를 이루는 세 점의 결합은 삼각형이 아닌 선분을 만들어낸다.
- 이러한 삼각형을 퇴화삼각형(Degenerate triangle)이라 한다.
- 퇴화삼각형이 검출되면 그리기에서 제외한다.
텍스처 매핑
- 무게중심좌표는 메시에 이미지를 입히는 용도로 활용할 수 있다.
- 메시에 이미지를 입히기 위해 변환된 데이터를 텍스처(Texture)라고 한다.
- 메시에 이미지를 입히는 작업을 텍스처 매핑(Texture mapping)이라 한다.
- 이미지를 메시에 입히기 위해 원본 해상도에 관계없이 텍스처의 가로, 세로 크기를 1로 정규화 한다.
- 텍스처를 구성하는 2차원 좌표계를 UV좌표계라고 한다. 가로정보는 U, 세로정보는 V로 지정된다.
UV 좌표
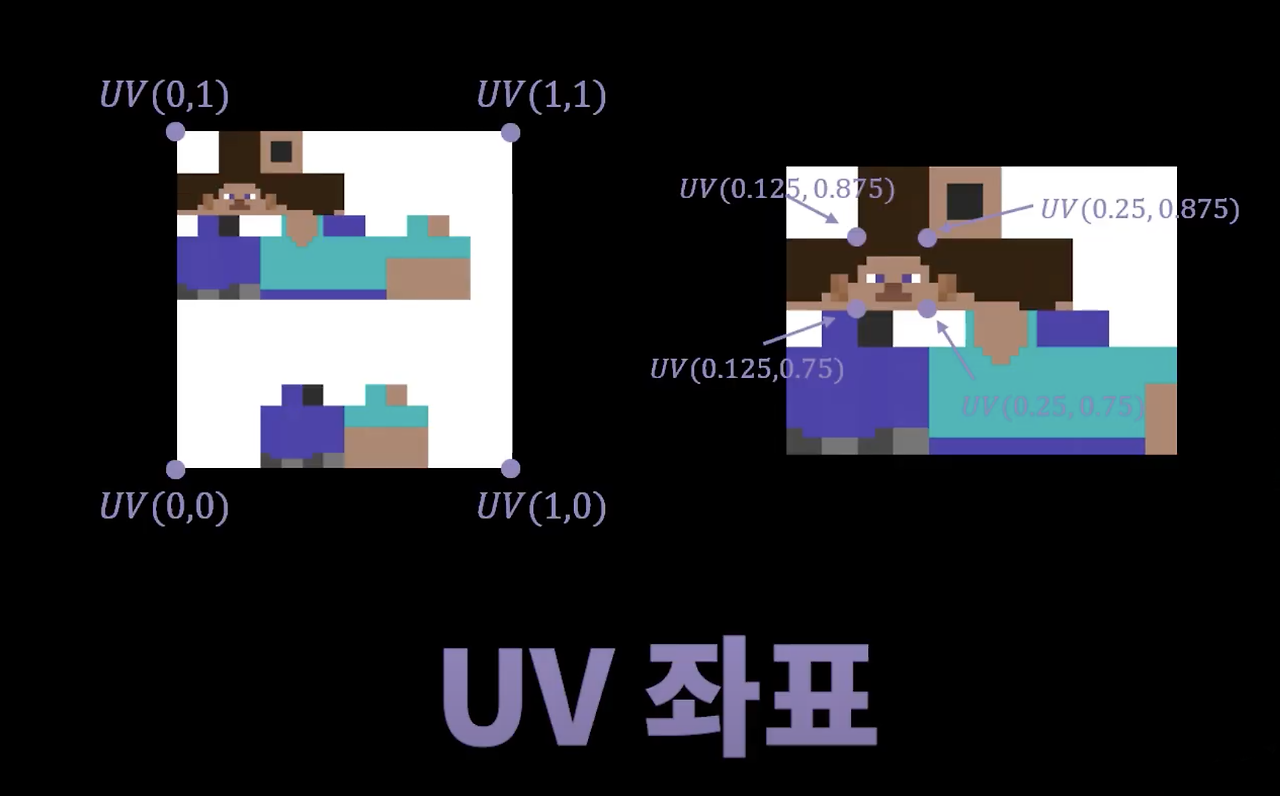
- 삼각형에 텍스처를 오려붙일 때 사용하는데 이 때 사용하는 좌표를 UV좌표라고 한다.

- 위 그림은 사각형 텍스처의 영역을 삼각형에 대응하여 표현한 그림이다.
- 각 점에 대응하는 이미지의 2차원 좌표를 삼각형에 보배하듯이 붙여넣는다.
- 삼각형의 정점에 지정한 좌표들을 붙여주면 삼각형 내부 영역은 앞서 이야기한 무게중심좌표를 사용해 적절한 텍스처를 채워넣을 수 있다.
- 이렇게 삼각형을 구성하는 세 점에 색상이나 UV 같은 정보들을 넣어서 삼각형 내부를 칠하는 효과를 만들 수 있다.
물체를 화면에 그리는 과정
- 물체를 3개의 정점으로 구성된 삼각형으로 분리한다.
- 그리고 삼각형을 각각 그려서 화면을 채운다.
- 이 과정은 정형화되어 있기 때문에 보통 렌더링 파이프라인이라고 부르고 그래픽카드가 모두 자동으로 처리해준다.
- 하지만 그래픽의 응용력을 높이기 위해서 파이프라인 중간에 개발자가 원하는 기능을 추가할 수 있는 두 가지 명령 집합이 있다.
- 그것들이 바로 정점 셰이더(Vertex Shader)와 픽셀 셰이더(Pixel Shader)이다.
- 정점 셰이더
- 삼각형을 구성하는 각 정점의 최종 데이터를 확정하는 함수
- 픽셀 셰이더
- 삼각형 내부를 구성하는 각 픽셀의 최종 색상을 확정하는 함수
- 각 픽셀들은 앞에서 설명한 무게중심좌표에 의해 계산된 값이 자동으로 들어오게 된다.
- 이 값과 텍스처의 값 조명 등의 값이 서로 결합하여 다양한 효과를 연출할 수 있다.
출처
https://m.yes24.com/Goods/Detail/107025224
이득우의 게임 수학 - 예스24
39가지 실시간 렌더링 게임 프로그래밍 실습 예제를 하나씩 따라 해보며 독자가 직접 체득하는 흥미로운 게임 수학의 세계! 게임 개발자와 그래픽 아티스트들이 궁금해 했던 3D 가상 세계와 메타
m.yes24.com
https://wecandev.tistory.com/211
[이득우 게임수학] 8. 삼각형 : 물체를 구성하는 가장 작은 단위
8.1 세점의 결합 세점 P1, P2, P3 를 결합하는 경우 스칼라는 2개에서 3개로 늘어나는데 세 스칼라의 합은 1이 되어야 하므로 아핀 결합식은 다음과 같이 전개 된다. P` = s·P1 + t·P2 + (1-s-t)·P3 (P` - P3) =
wecandev.tistory.com
https://windarea.tistory.com/56
3D 모델링의 종류 - Wire, Surface, Solid
3D 모델링에는 크게 3가지로 나눌 수 있습니다. 1. 와이어 프레임 모델링 (Wire Frame Modeling) 2. 서피스 모델링 (Surface-based modeling) 3. 솔리드 모델링 (Solid Modeling) 비교 항목 와이어프레임 (Wireframe) 서피
windarea.tistory.com
[게임수학의 이해 이득우 교수님 강의 정리] 3. 물체의 수학 Ⅱ : 정점과 삼각형
3차원 공간의 이동 구현을 위해서는 물체를 표현하는 3차원 + 이동을 표현하는 1차원총 4차원의 공간이 필요함4차원 공간을 그림으로 표현할 수가 없음.그래서 2차원 공간의 이동 구현으로 대신
velog.io
'게임수학' 카테고리의 다른 글
| [게임수학] 벡터의 외적 (0) | 2024.04.23 |
|---|---|
| [게임수학] 3차원 공간 (0) | 2024.04.23 |
| [게임수학] 벡터의 내적 (0) | 2024.04.22 |
| [게임수학] 어파인 공간(Affine space) (0) | 2024.04.22 |
| [게임수학] 행렬 (1) | 2024.04.22 |
