내적(Dot product)
- 벡터의 내적(Dot product)은 같은 차원의 두 벡터가 주어졌을 때 벡터를 구성하는 각 성분을 곱한 후 이들을 더해 스칼라를 만들어내는 연산이다.
u = (a,b)
v = (c,d)
u·v = a·c + b·d내적의 성질
- 내적은 스칼라의 곱셈과 덧셈으로 구성되어 있으므로 교환법칙이 성립한다.
- 하지만 결과가 벡터가 아닌 스칼라로 나오는 성질로 인해 결합법칙은 성립하지 않는다.
u·v = a·c + b·d
v·u = c·a + d·b
∴ u·v = v·u
u·(v·w) ≠ (u·v)·w- 내적은 덧셈에 대한 분배법칙이 성립된다.
w·(u+v) = (e,f)·(a+c, b+d) = ae + ce + bf + df
u·w + v·w = (a,b)·(e,f) + (c,d)·(e,f) = ae + bf + ce + df
∴ w·(u+v) = u·w + v·w- 같은 벡터를 내적하면 벡터의 크기를 제곱한 결과가 나온다.
(x,y)·(x,y) = x^2 + y^2
∴ v·v = |v|^2- 내적은 교환법칙과 분배법칙이 성립하기 때문에, 두 벡터 합의 내적은 두 벡터의 크기로 표현할 수 있다.
(u+v)·(u+v) = u·u + v·v + 2(u·v)
= |u|^2 + |v|^2 + 2(u·v)- 벡터의 내적은 벡터를 응용하는데 있어 빈번히 사용되는 중요한 공식
- 곱셈과 덧셈으로만 구성된 내적은 컴퓨터에서 빠르게 처리되기 때문에 컴퓨터 그래픽에서 실시간으로 변화하는 효과를 구현하는데 유용하게 사용된다.
내적과 삼각함수

- 벡터의 내적은 두 벡터의 사잇각에 대한 cos 함수와 비례하는 특징을 가진다.
- 두 벡터 u,v의 사잇각을 θ라고 할 때 내적과 cos 함수의 관계는 다음과 같다
u·v = |u||v|cosθ- 내적의 정릴은 덧셈과 곱셈만 사용해 cos함수 값을 빠르게 계산할 수 있어 유용하게 활용된다.
- 벡터가 영벡터가 아닌 경우, 내적 값이 0이 되기 위한 조건은 cos 함수 값이 0이 되는 경우 뿐
- 두 벡터의 사잇각이 90도 혹은 270도인 경우다.
- 즉, 두 벡터가 서로 직교하는 경우 뿐
- 직교성을 판별할 수 있는 내적의 성질은 많은 곳에서 응용된다.
- 벡터 공간에서 직교하는 두 표준기저벡터를 내적한 결과는 0이 나온다.
- 두 표준 기저벡터를 각 θ만큼 회전한 두 기저벡터도 서로 직교한다.
행렬 곱을 내적으로 표현
- 행렬과 벡터의 곱셈은 행렬을 구성하는 두 개의 행벡터 (a, b), (c, d)와 벡터를 구성하는 열벡터 (x, y)의 내적으로 표현 가능
┌ a b ┐┌ x ┐ = ┌ ax + by ┐
└ c d ┘└ y ┘ └ cx + dy ┘
┌ ax + by ┐ = ┌ (a,b)·(x,y) ┐
└ cx + dy ┘ └ (c,d)·(x,y) ┘- 행렬의 곱셈 또한 벡터의 내적으로 바꿔 표현할 수 있다.
┌ a b ┐ ┌ e f ┐ = ┌ ae + bg af + bh ┐ = ┌ (a,b)·(e,g) (a,b)·(f,h) ┐
└ c d ┘ └ g h ┘ └ ce + dg cf + dh ┘ └ (c,d)·(e,g) (c,d)·(f,h) ┘- 직교 행렬(Orthogonal matrix)은 정방행렬을 구성하는 모든 행벡터와 열벡터의 크기가 1이고 벡터들이 서로 직교하는 행렬이다.
- 직교행렬의 정의에 의해 벡터 (a,b)와 (c,d)는 서로 직교하므로 두 벡터의 내적은 0이 나온다.
- 직교행렬의 전치행렬은 역행렬이 된다.
- 따라서 직교행렬과 그 전치행렬의 곱은 언제나 항등행렬을 보장한다.
- 회전 변환행렬은 각 행벡터와 열벡터의 크기가 1이고 서로 직교하므로 직교행렬이다.
- 여러 종류의 선형 변환중 물체의 형태가 그대로 유지되는 선형 변환을 강체 변환(Rigid Transformation)이라고 한다.
- 변화된 기저벡터의 크기는 모두 1이어야 한다.
- 모든 기저벡터는 서로 직교해야 한다.
- 행렬식 값이 1이어야 한다.
- 회전 변환은 직교행렬의 성질을 가지고 있으며, 행렬식 ad - bc는 언제나 1이 된다.
- 즉, 물체의 형태를 그대로 유지시켜주는 강체 변환이다.
det(R) = cos^2θ + sin^2θ = 1시야 판별
앞뒤 판별
- 게임 제작 과정에서 공간을 파악하는데 가장 유용하게 활용되는 사례는 목표물이 캐릭터의 앞에 있는지 뒤에 있는지 구분하는 것
- 이는 내적의 부호를 통해 쉽게 파악할 수 있다.
- 내적과 삼각함수와의 관계의 식인 |u||v| cosθ 식을 살펴보면
- 벡터의 크기 값은 언제나 양수이므로 벡터 내적의 부호는 cos 함수가 결정하는 것을 알 수 있다.
- cos 함수는 (-90, 90) 영역에 대해 양의 부호를 가지고 -90와 90에서는 0, 나머지 범위에서는 음의 부호를 가진다.

- 벡터의 내적 부호는 두 벡터가 이루는 사잇각의 범위에 따라 결정될 것이다.
- 첫 번째 벡터를 캐릭터의 시선 방향으로 생각한다면 두 번째 벡터는 시선 벡터에서 멀어질수록 사잇각이 커질 것
- 두 번째 벡터가 보라색으로 칠해진 영역에 존재한다면 내적 값은 언제나 양의 부호를 가진다.
- 벡터 내적의 부호만 가지고도 두 벡터가 같은 방향을 향하는지 아니면 서로 마주보는지 확인할 수 있다.
- 벡터 내적의 결과가 양수 : 두 벡터는 같은 방향을 향하고 있다.
- 벡터 내적의 결과가 음수 : 두 벡터는 다른 방향을 향하고 있다.
- 벡터 내적의 결과가 0 : 두 벡터는 서로 직교한다.

- 캐릭터의 시선을 f 캐릭터에서 목표물로 향하는 벡터를 v라고 할때 두 벡터의 내적 f·v 의 부호에 따라 캐릭터와 목표물 사이의 공간 구성을 파악할 수 있다.
- f·v 결과의 부호가 양수 : 캐릭터 앞에 목표물이 있다.
- f·v 결과의 부호가 음수 : 캐릭터 뒤에 목표물이 있다.
- f·v 결과가 0 : 캐릭터 바로 옆에 목표물이 있다.
시야 범위 판별

- 케릭터에 부여한 시야각이 β라면 양쪽으로 균일하게 β/2의 시야각이 설정될 것
- 나머지는 앞뒤 판별 문제와 동일하게 캐릭터의 시선 단위벡터를 f, 캐릭터에서 목표물로 향하는 단위벡터를 v라고 할 경우 벡터 f와 벡터 v의 사잇각을 α로 설정한다.
- 사잇각 α가 사야각의 절반인 β/2보다 작거나 같은지 비교하면 캐릭터 시야에 목표물이 탐지되는지 알 수 있다.
- 내적에 비례하는 cos 함수는 [0, 180] 범위에서는 각이 커질수록 값이 작아지는 성질을 지닌다.
- 각이 작을수록 cos 함수의 값은 반대로 커진다.
- 캐릭터의 시야에 목표물이 탐지되는지 판별하는 과정은 다음과 같다.
- 시야각을 절반 나눈 각의 cos(β/2)를 미리 계산해둔다.
- 캐릭터의 시선 벡터를 구하고 벡터의 크기를 1로 정규화시킨다.
- 캐릭터에서 목표물로 향하는 벡터도 정규화시킨다.
- 정규화시킨 벡터의 내적 결과는 cos(α)가 된다. 이를 cos(β/2)값과 비교
- 사잇각을 몰라도 내적 f · v의 결과에 따라 캐릭터 시야 범위에 목표물이 있는지 파악할 수 있다.
- f · v >= cos(β/2) : 목표물이 시야 범위 안에 있음
- f · v < cos(β/2) : 목표물이 시야 범위 밖에 있음
- atan2 함수를 활용해도 구할 수 있지만 단위벡터를 통해 내적을 계산하는 방식이 더 효율적이다.
조명 효과 구현

- 램버트 반사(Lambertian reflection)모델은 현실 세계와 비슷한 조명 효과를 만들기 위해 스위스의 수학자 요한 하인리히 램버트(Johann Heinrich Lambert)가 고안하였다.
- 램버트 반사 모델은 컴퓨터 그래픽스에서 표면에서의 조명 모델 계산을 위해 쓰인다.
- 계산량이 적어 속도가 빠르지만 그럴듯한 조명 효과를 줄 수 있어 실시간 조명 구현이 필요한 게임 제작에 널리 사용
- 빛을 받아 표면에서 반사되는 빛의 세기는 두 벡터가 만드는 사잇각의 cos 함수에 비례한다는 내용이다.
- 표면이 향하는 단위벡터를 N으로 지정하고 표면에서 광원으로 향하는 단위 벡터를 L로 지정한다면 두 벡터의 내적을 사용하여 사잇각 cos 값을 얻을 수 있다.
N · L = cosθ투영 벡터
- 벡터 내적은 어떤 벡터를 다른 벡터에 직교 투영하는 용도로 사용된다.

- 위 그림과 같이 카메라가 만드는 공간을 분석할 때 카메라와 물체 사이의 거리 외에도 카메라에서 물체까지의 깊이 값이 필요한 경우가 있다.
- 이 경우 내적을 활용한 투영 벡터를 구하는 공식이 활용된다.

- 내적을 통해 투영 벡터를 구하는 공식 유도
- 임의의 두 벡터 u와 v가 주어졌을 때 벡터 u를 벡터 v에 투영하는 상황인 경우
- 투영한 벡터 v'은 대상 벡터 v와 방향이 같다.
- 투영한 벡터 v'의 크기는 벡터 v를 정규화시킨 단위 벡터 v를 구하고 그 크기를 곱하면 얻을 수 있다.
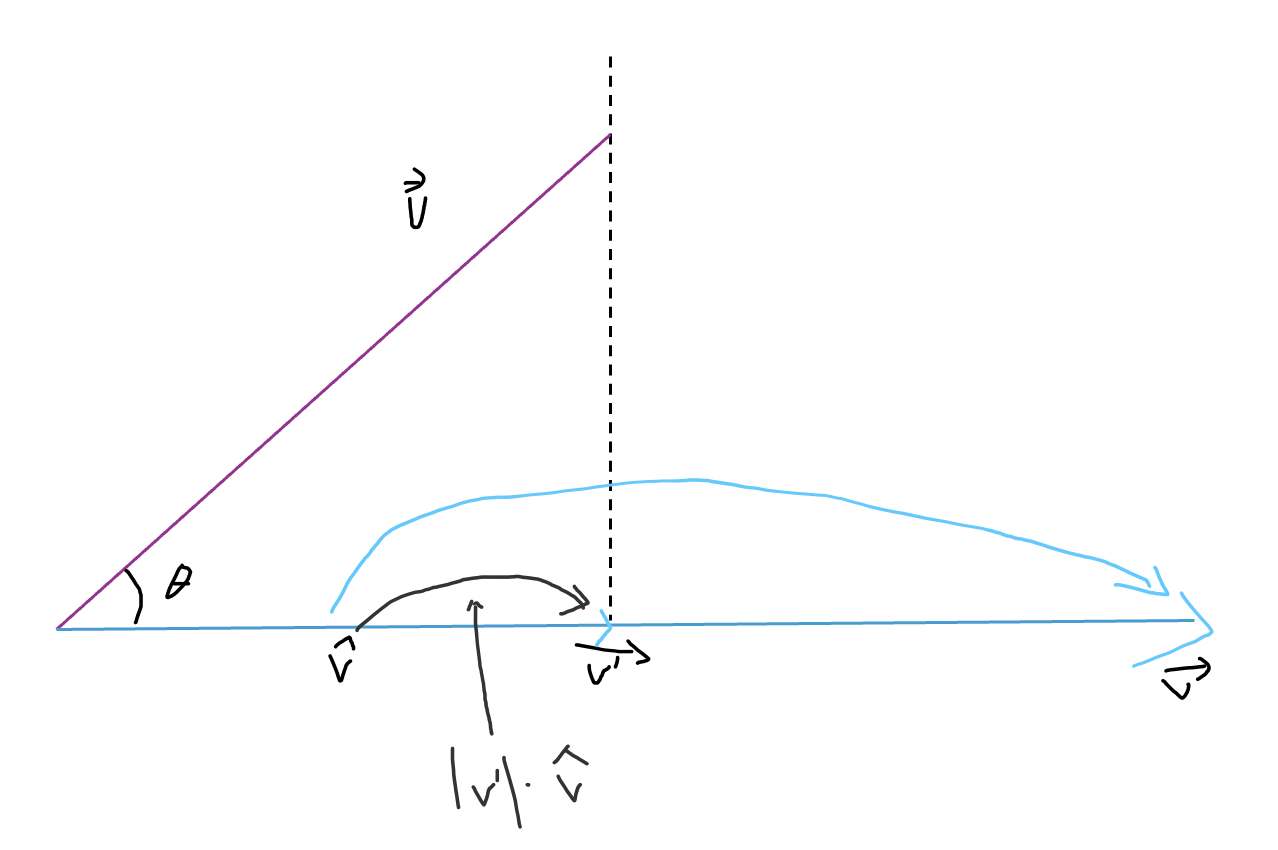
- 위를 그림을 수식으로 표현하면 다음과 같다.
v' = |v'|·hat(v)- 내적을 활용해 u로부터 v'를 구하도록 수식을 전개하면 다음과 같다.
v' = |v'|·hat(v)
= |v'|·(v/|v|) // 단위벡터 v를 구하기 위해 벡터 v를 정규화
= |u|·cosΘ·(v/|v|) // v'의 크기는 벡터 u의 크기에 cosΘ를 곱해 얻을 수 있음
= |u|·(u·v/|u||v|)·(v/|v|) // cosΘ는 내적 공식으로부터 얻을 수 있음
= (u·v)/|v|^2 · v // 분자와 분모를 소거하고 정리
= (u·v)/(v·v) · v // 벡터의 크기의 제곱을 내적으로 변경- 투역할 벡터 v의 크기가 1인경우 위 식은 단순하게 정리된다.
v' = (u·v) · v
출처
https://m.yes24.com/Goods/Detail/107025224
이득우의 게임 수학 - 예스24
39가지 실시간 렌더링 게임 프로그래밍 실습 예제를 하나씩 따라 해보며 독자가 직접 체득하는 흥미로운 게임 수학의 세계! 게임 개발자와 그래픽 아티스트들이 궁금해 했던 3D 가상 세계와 메타
m.yes24.com
https://wecandev.tistory.com/209
[이득우 게임수학] 7. 내적: 벡터 공간의 분석과 운용
벡터 내적의 계산법과 내적이 가지는 성질을 알아보고 삼각함수와 어떤 연관성을 가지는지 알아보자 7.1 벡터의 내적 벡터의 내적(Dot product)은 같은 차원의 두 벡터가 주어졌을 때 벡터를 구성하
wecandev.tistory.com
https://gaussian37.github.io/math-la-projection/
벡터의 내적 (inner product)와 벡터의 정사영 (projection)
gaussian37's blog
gaussian37.github.io
[면접기술] 벡터의 외적과 내적
게임 프로그래밍에서 왜 벡터를 쓰는가?게임상의 오브젝트들의 정보를 나타낼 때, 좀 더 간단하고 편하게 나타내기 위해서 사용.벡터로 속도, 바람, 저항, 충돌, 위치 판단 등 많은 것들을 표현
velog.io
'게임수학' 카테고리의 다른 글
| [게임수학] 3차원 공간 (0) | 2024.04.23 |
|---|---|
| [게임수학] 정점과 삼각형 (1) | 2024.04.23 |
| [게임수학] 어파인 공간(Affine space) (0) | 2024.04.22 |
| [게임수학] 행렬 (1) | 2024.04.22 |
| [게임수학] 삼각함수 (1) | 2024.04.22 |
