선형성?
- 벡터와 스칼라 곱으로 생성된 벡터는 벡터와 평행한 원점을 지나는 일직선 상에 위치한다.
- 이러한 성질을 선형성(Linearity)라고 한다.
- 수학에서는 선형성을 가법성(Additivity)과 1차 동차성(Homogeneity of degree1) 두 가지 조건을 모두 만족하는 함수의 성질로 정의한다.
f(x1 + x2) = f(x1) + f(x2) // 가법성
f(k · x) = k · f(x) //1차 동차성선형함수
- 원점을 지나는 직선 함수가 있다고 생각해보자
f(x) = ax
y = ax // 출력의 원소를 y로 표시 (직선 방정식)
// 선형성의 첫 번째 성질인 가법성 검증
// 좌변과 우변의 값이 동일한지 확인하는 것으로 판별 가능
f(x1 + x2) = a(x1 + x2) //좌변
f(x1) + f(x2) = ax1 + ax2 //우변
// 선형의 두 번째 성질인 1차 동차성 검증
// a, x, k가 모두 체의 성질을 가지는 실수인 경우
// 체는 곱셈에 대해 결합법칙과 교환법칙이 성립
f(kx) = a(kx) //좌변
kf(x) = k(ax) //우변- 위 식에서 증명했듯 y = ax는 선형성을 만족하는 것을 알 수 있다.
- f(x) = x^2와 같은 곡선의 함수도 선형성을 만족하는지 판별해보자
f(x1 + x2) = (x1 + x2)^2 = x1^2 + x2^2 + 2x1x2 //좌변
f(x1) + f(x2) = x1^2 + x2^2 //우변- 위 함수는 좌우변의 결과가 다르므로 선형성을 만족하지 않는다.
- f(x) = ax 에 스칼라 b를 더한 f(x) = ax + b는 선형성을 만족하는지 확인해보자
f(x1 + x2) = a(x1 + x2) + b //좌변
f(x1) + f(x2) = ax1 + ax2 + 2b //우변- 위 함수는 b만큼의 차이 때문에 가법성을 만족하지 않는다.
- 선형성이란 곧게 뻗은 직선의 성질을 뜻하는 것이 아니라, 두 집합의 순수한 비(Ratio)로 구성된 1차적 대응관계를 의미한다.
- 함수 f(x) = ax에서 대응되는 두 집합은 순수한 비로 구성되어 있기 때문에 다른 입력값을 투여했을 때 어떤 출력값이 나올지 쉽게 예측할 수 있음
- 반대로 역함수 f(x) = 1/a(x)를 사용하면 출력값으로부터 입력값을 거꾸로 계산하는 것이 가능함
벡터 공간의 선형 변환
- 정의역에 해당하는 벡터 공간을 V, 그 원소를 v로, 공역에 해당하는 벡터 공간을 W, 그 원소를 w로 표시하고 두 벡터 공간의 대응관계를 표현하면 다음과 같다.
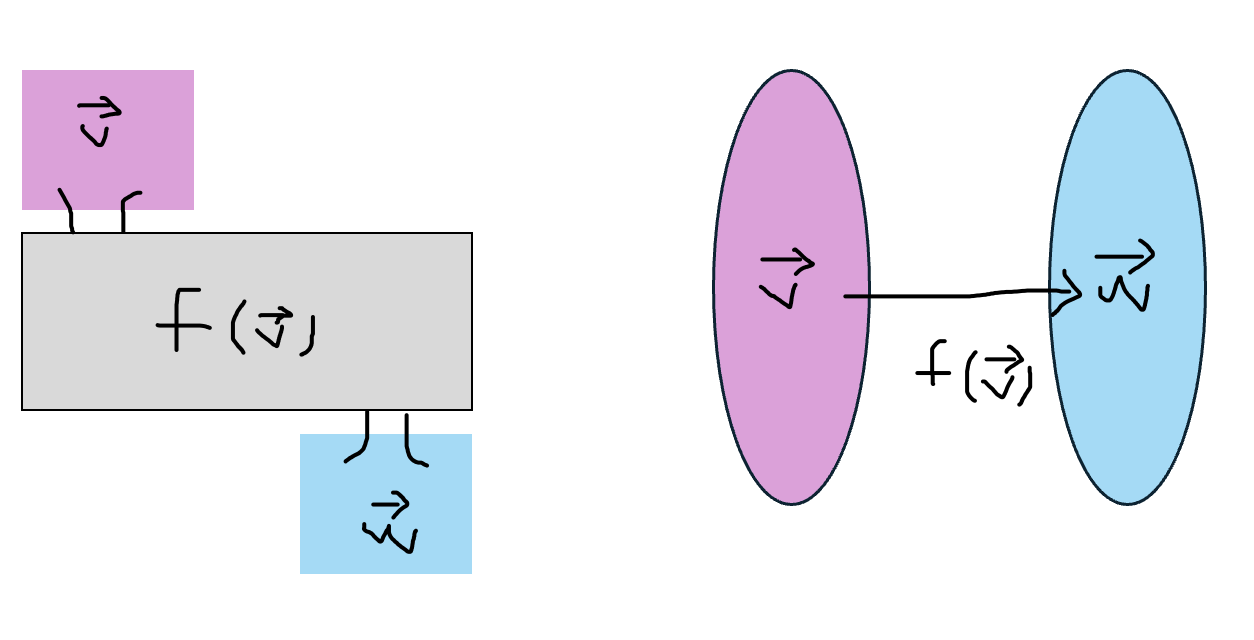
- 입력에 사용한 2차원 벡터가 (x, y)로 구성되어 있는 경우, x와 y는 물과 기름과 같이 서로 독립된 관계를 형성한다.
- 선형성을 가지는 함수는 순수한 비의 형태로 구성되어 있다.
- x와 y 각각에 대해 선형성을 유지하고자 한다면 이들은 ax와 by 같은 단순 비의 형태를 사용할 것
- 이를 섞은 최종 결과는 각 비의 결과를 더한 ax + by의 형태가 될 것
- 따라서 2차원 벡터를 입출력으로 사용하는 선형성을 가지는 함수는 다음과 같이 설계될 것
f(V) = f(x, y) = (ax + by, cx + dy)- 위 함수가 가법성을 만족하는지 검증하면 아래와 같다.
//가법성 검증
f(v) = f(x,y) = (ax + by, cx + dy)
f(v1 + v2) = f(x1 + x2, y1 + y2)
= (a(x1 + x2) + b(y1 + y2), c(x1 + x2) + d(y1 + y2)) //좌변
f(v1) + f(v2) = (ax1 + by1, cx1 + dy1) + (ax2 + by2, cx2 + dy2)
= (ax1 + ax2 + by1 + by2, cx1 + cx2 + dy1 + dy2) //우변
∴ f(v1 + v2) = f(v1) + f(v2)
//1차 동차성 검증
kf(v) = (kax + kby, kcx + kdy) //좌변
f(kv) = (akx + bky, ckx + dky) //우변
∴ f(v1 + v2) = f(v1) + f(v2)- 함수 f(x, y)는 가법성과 1차 동차성을 만족하므로 선형함수다.
- 표준기저벡터의 선형 결합으로 형성된 벡터 공간은 선형성을 지닌다.
- 이 벡터 공간을 선형 함수로 변화시킨 새로운 공간도 기저벡터의 선형 결합으로 형성되므로 선형성을 지닌다.
- 두 공간이 동일한 구조를 지닐 때 두 공간의 대응 관계를 변환(Transformation)이라 한다.
- 아래처럼 선형성을 유지시켜주는 선형함수는 선형 변환(Linear transformation)이라고 한다.
- 벡터 공간에서 발생하는 선형 변환의 원리는 크기 변환이나 회전 변환과 관련이 있다.
- 임의의 벡터 V의 크기를 k배 늘리는 작업은 스칼라 곱셉으로 표현이 가능하다.
- f(V) = f(x, y) = (kx, ky)
- 이는 (ax + by, cx + dy) 형식에 a = k, b = 0, c = 0, d = k를 대입한 결과와 동일하므로 선형 변환이다.
- 임의의 벡터 V를 각θ 만큼 회전시키는 작업은 다음과 같은 함수로 표현이 가능
- f(V) = f(x, y) = (cosθ·x - sinθ·y, sinθ·x + cosθ·y)
- 이는 a = cosθ, b = -sinθ, c = sinθ, d = cosθ를 대입한 결과이므로 선형 변환이다.
- 벡터 공간에서의 선형변환은 단순 비례 관계로 구성된 선형 함수 f(x) = ax처럼 두 집합의 순수한 비를 통해 예측할 수 있는 형태로 변환된다.
- 역함수를 통해 변환 후의 벡터로부터 변환 전의 벡터를 파악할 수 있다.
- 선형 변환의 원리는 게임의 가상세계를 구축하는데 필요한 모든 변환의 기본 바탕이 된다.
- 선형 변환을 안정적이고 빠르게 계산할 수 있는 체계가 구축된다면 컴퓨터를 사용해 게임이 요구하는 가상 세계의 기반을 손쉽게 구축할 수 있음
- 선형 변환의 계산 과정을 체계화하여 손쉽게 계산할 수 있는 도구가 행렬이다.
행렬?
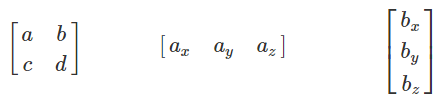
- 행렬(Matrix)은 수를 사각형의 형태로 행과 열을 맞춰 배열한 테이블이다.
- n개의 행과 m개의 열로 구성된 반듯한 사각형의 형태를 띤다.
- 행렬은 선형 변환과 벡터를 나타내는데 사용된다.
- 벡터는 한 줄로 구성된 행렬로 표현되며, 가로와 세로 두 가지 표현 방식이 존재한다.
- (x, y)로 구성된 2차원의 벡터는 A와 같이 열벡터로 표현되거나 B와 같이 행벡터로 표현될 수 있다.
A = ┌ x ┐ B = [ x y ]
└ y ┘- 선형 변환을 표현할 때는 행과 열의 크기가 같은 정방행렬(Square matric)을 사용한다.
- 2차원 벡터 공간의 선형 변환 f(x, y) = (ax + by, cx + dy)는 2 x 2크기의 정방행렬로 표현된다.
A = ┌ a b ┐
└ c d ┘- 정방행렬 A는 2개의 행벡터 또는 2개의 열벡터로 구성된다고 할 수 있다.
- 정방행렬 A를 행벡터와 열벡터로 분석하면
- 첫 번째 행벡터는 (a, b), 두 번째 행벡터는 (c, d)이다.
- 첫 번째 열벡터는 (a, c), 두 번째 열벡터는 (b, d)가 된다.
행렬의 기본 연산
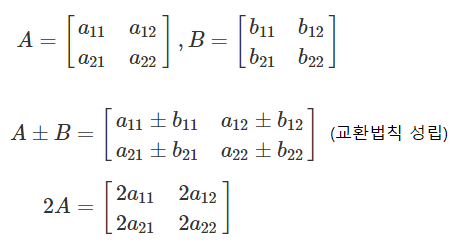
- 반드시 알아야 하는 행렬의 연산은 아래 4가지다.
- 행렬과 행렬의 덧셈
- 행렬과 스칼라의 곱셈
- 행렬의 전치(Transpose)
- 행렬과 행렬의 곱셈
//행렬과 행렬의 덧셈
A + B = ┌ a b ┐ + ┌ e f ┐ = ┌ a + e b + f ┐
└ c d ┘ └ g h ┘ └ c + g d + h ┘
//행렬과 스칼라의 곱셈
k · A = k · ┌ a b ┐ = ┌ k · a k · b ┐
└ c d ┘ └ k · c k · d ┘
//행렬의 전치
┌ a d ┐T
│ b e │ = ┌ a d c ┐
└ c f ┘ └ d e f ┘
//전치 행렬은 행과 열의 같은 번호끼리 교환하는 것행렬의 곱
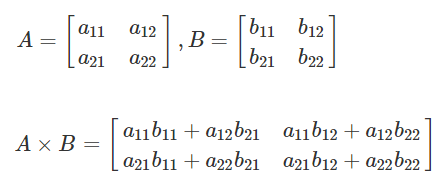
- 행렬의 곱셈은 앞에 위치한 행렬의 행벡터와 뒤에 위치한 행렬의 열벡터를 각각 곱하는 방식으로 진행된다.
- 행렬 곱셈의 중요한 성질 중 하나는 교환법칙이 성립하지 않는다는 점이다.
- 그러나 결합법칙은 만족한다.
- 행렬의 곱은 행렬의 내적과 같다.
//교환 법칙
A · B = ┌ a b ┐ · ┌ e f ┐ = ┌ ae + bg af + bh ┐
└ c d ┘ └ g h ┘ └ ce + dg cf + dh ┘
B · A = ┌ e f ┐ · ┌ a b ┐ = ┌ ae + cf be + df ┐
└ g h ┘ └ c d ┘ └ ag + ch bg + dh ┘
∴ A · B ≠ B · A
//결합 법칙
A · (B · C) = ┌ a b ┐ · ( ┌ e f ┐ · ┌ i j ┐ )
└ c d ┘ ( └ g h ┘ └ k l ┘ )
= ┌ a b ┐ · ┌ ei + fk ek + fl ┐
└ c d ┘ └ gi + hk gj + hl ┘
= ┌ aei + afk + bgi + bhk aej + afl + bgj + bhl ┐
└ cei + cfk + dgi + dhk cej + cfl + dgj + dhl ┘
(A · B) · C = ┌ a b ┐ · ( ┌ e f ┐ · ┌ i j ┐ )
└ c d ┘ ( └ g h ┘ └ k l ┘ )
= ┌ a b ┐ · ┌ ei + fk ek + fl ┐
└ c d ┘ └ gi + hk gj + hl ┘
= ┌ aei + afk + bgi + bhk aej + afl + bgj + bhl ┐
└ cei + cfk + dgi + dhk cej + cfl + dgj + dhl ┘
∴ (A · B) · C = A · (B · C)- 다른 특징 중 하나는 행렬 곱을 전치한 결과는 순서를 바꾼 후 각각 전치해 곱한 결과와 동일하다.
//중략
∴ (A · B)^T = B^T · A^T정방 행렬의 곱셈
- 2 x 2 정방행렬이 2차원 벡터 공간의 선형 변환에 대응된다면, 2 x 2 정방행렬 간의 곱은 합성함수에 대응되는 연산이다.
- 백터 v에 선형 변환을 나타내는 2 x 2 정방행렬 A, B를 순서대로 연산한다면, 수식은 아래와 같다.
- B · A · v
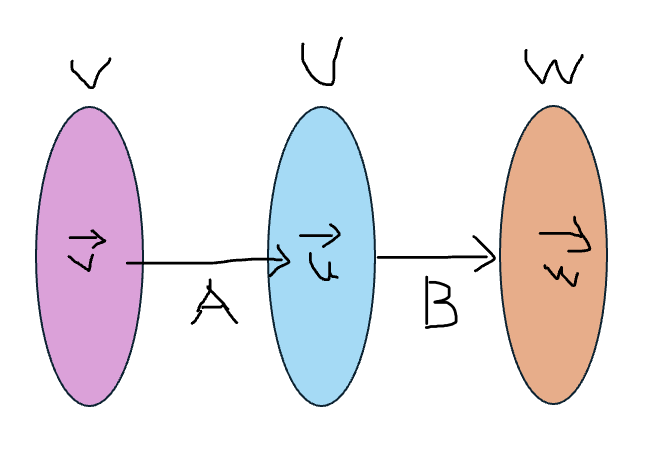
- 이는 위 그림과 같이 세 개의 2차원 벡터 공간 V, U, W에 대해 두 번의 선형 변환을 거쳐 벡터 공간 V에 속한 벡터 v가 벡터 공간 W의 벡터 w에 대응되는 관계로 해석할 수 있다.
- 선형 변환을 담당하는 정방행렬 A, B와 벡터 v의 각 요소는 다음과 같이 행렬로 나타낼 수 있다.
B = ┌ e f ┐
└ g h ┘
A = ┌ a b ┐
└ c d ┘
v = ┌ x ┐
└ y ┘- 벡터 v가 벡터 w로 변환되는 과정은 다음과 같은 행렬 곱으로 표현할 수 있다.
w = ┌ e f ┐ · ┌ a b ┐ · ┌ x ┐
└ g h ┘ └ c d ┘ └ y ┘- 합성함수는 결합법칙을 만족하기 때문에, 합성함수에 대응하는 행렬의 곱셈도 결합법칙을 만족한다.
- 따라서 행렬의 연산 순서를 바꾸어도 최종 계산된 벡터 w 값은 동일함
A · v = ┌ a b ┐ · ┌ x ┐ = ┌ ax + by ┐
└ c d ┘ └ y ┘ └ cx + dy ┘
// 1번 식
B·(A·v) = ┌ e f ┐ · ┌ ax + by ┐ = ┌ e(ax+by) + f(cx+dy) ┐
└ g h ┘ └ cx + dy ┘ └ g(ax+by) + h(cx+dy) ┘
B · A = ┌ e f ┐ · ┌ a b ┐ = ┌ ae+cf be+df ┐
└ g h ┘ └ c d ┘ └ ag+ch bg+dh ┘
// 2번 식
(B·A)·v = ┌ x(ae+cf) + y(be+df) ┐
└ x(ag+ch) + y(bg+dh) ┘- 1번 식과 2번 식은 동일한 값이므로 다음 식이 성립
w = B · (A · v) = (B · A) · v- 결합 법칙이 성립하는 행렬 곱의 성질은 컴퓨터 그래픽 연산에서 아주 유용하게 활용된다.
- 100개의 점으로 구성된 물체가 모니터에 표현되기 까지 5번의 선형 변환이 발생한다고 가정
- 물체의 점을 각각 v1, ..., v100으로 표기
- 선형 변환을 수행하는 행렬을 각각 A, B, C, D, E라고 하면
컴퓨터가 수행할 연산은 다음과 같다.
E · D · C · B · A · v1
...
E · D · C · B · A · v100- 각 점마다 5번의 행렬 곱이 수행되므로 100개 점에 대한 행렬 곱의 총 횟수는 500이 될 것
- 이때 결합 법칙이 성립하는 행렬 연산의 특징을 이용하면 계산량을 줄이되 동일한 결과를 얻을 수 있다.
- 행렬 곱을 4번 수행해서 합성함수에 해당하는 행렬 F를 미리 만든다.
- F = E · D · C · B · A
- 이제 각 점에 대해 미리 계산된 행렬 F만 곱하면 동일한 결과가 나온다.
컴퓨터가 수행할 연산은 다음과 같다.
F · v1
...
F · v100- 각 점에 대한 행렬 곱 횟수는 최초 합성 변환을 만들기 위한 4번의 행렬 곱과 벡터마다 1번의 행렬 곱이 수행되어 104가 된다.
- 정리하면 행렬은 컴퓨터 그래픽스에서 가상 세계를 구축하는데 필요한 계산량을 크게 줄여주는 역할을 함
행렬의 설계
- 평면상의 물체를 원하는 형태로 변환하기 위해 2 x 2 행렬을 설계하는 방법
- 벡터 공간 V를 구성하는 두 표준기저벡터 (1, 0)과 (0, 1)은 선형 변환을 통해 새로운 벡터 공간 W의 벡터 (a, b)와 (c, d)에 대응되어 변환된다면
- 벡터 공간 V의 벡터 v = (x, y)는 아래와 같은 표준기저 벡터의 선형 결합을 통해 생성된다.
v = (x,y) = x · (1,0) + y ·(0,1)
// 선형 변환
w = x(a,c) + y(b,d) = (ax + by, cx + dy)
// 이는 a, b, c, d로 만들어진 정방행렬에 벡터(x, y)를 곱한 결과와 동일
┌ a b ┐ · ┌ x ┐ = ┌ ax + by ┐
└ c d ┘ └ y ┘ └ cx + dy ┘- 위 정방행렬과 표준기저벡터가 변환된 두 벡터 (a, c)와 (b, d)와의 관계를 분석해보면 이들은 정방행렬을 구성하는 열벡터임을 알 수 있다.
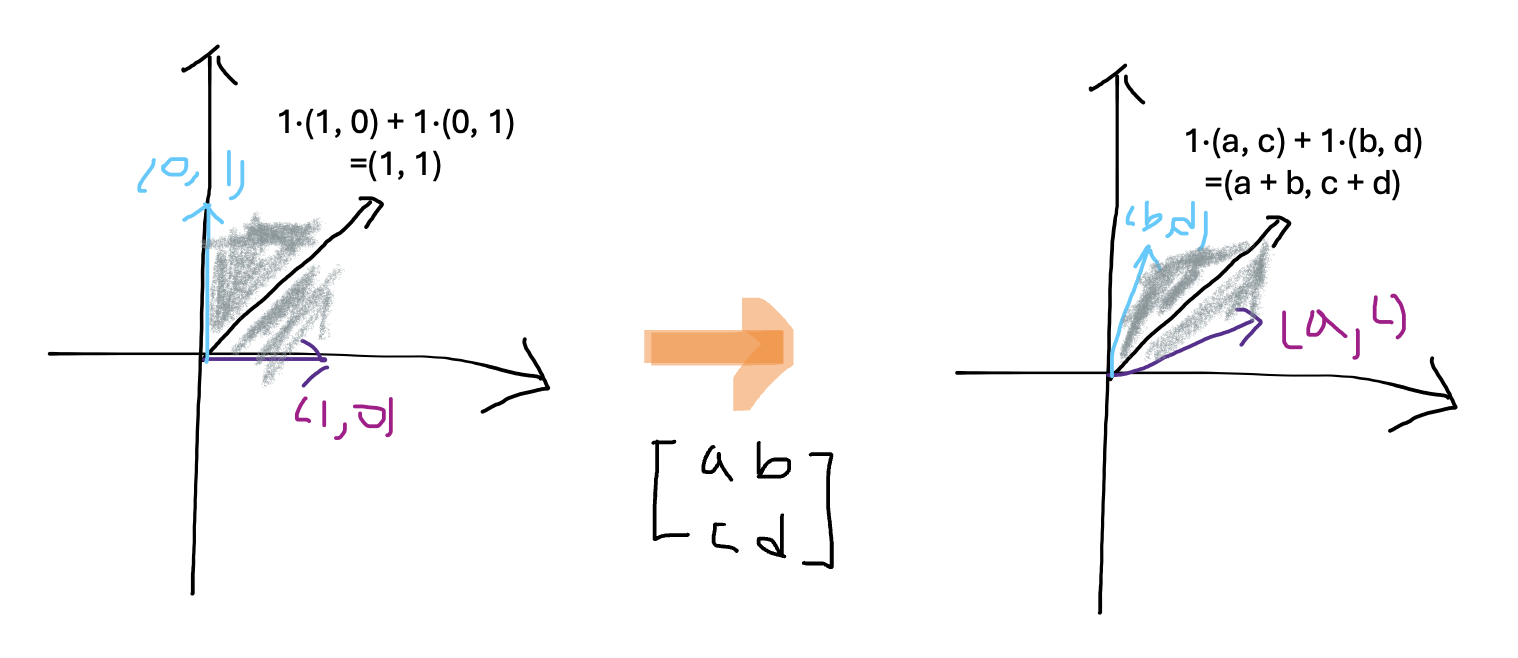
- 벡터 공간 V의 (0, 0)에서 (1, 1)까지로 둘러싸인 사각형의 부분 공간은 선형 변환을 통해 부분 공간이 변환된다.
- 선형 변환을 통해 원하는 형태로 공간이 변화되도록 행렬을 스스로 설계할 수 있다.
인접 행렬
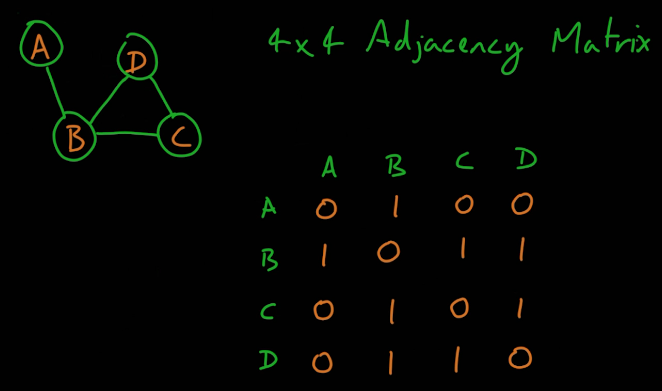
- 그래프 탐색으로 길을 찾을때 사용될 수 있다.
크기 변환 행렬
- 크기 변환행렬(Scale transformation matrix)은 물체의 크기를 변경하는 행렬이다.
- 크기 변환은 각 표준기저벡터를 동일한 방향으로 지정한 크기만큼 늘리는 변환을 의미한다.
- 이를 위해 (1,0)의 좌표를 갖는 e1과 (0,1)좌표를 갖는 e2의 두 표준기저벡터를 변환하면 아래와 같다.
a · (1,0) = (a,0)
b · (0,1) = (0,b)
S = ┌ a 0 ┐
└ 0 b ┘
// P = (x, y, z) 만큼 크기를 증가시키는 행렬
S = ┌ x 0 0 0 ┐
| 0 y 0 0 |
| 0 0 z 0 |
└ 0 0 0 1 ┘이동 행렬
- (x, y, z, 1) 벡터를 통해 이동 시킬 수 있다.
이동할 좌표가 P = (x, y, z)인 경우
// 일반적인 3D 공간에서의 이동 행렬
┌ 1 0 0 0 ┐
| 0 1 0 0 |
T = | 0 0 1 0 |
└ x y z 1 ┘
// 동차 좌표(Homogeneous Coordinates) 이동 행렬
┌ 1 0 0 x ┐
| 0 1 0 y |
T = | 0 0 1 z |
└ 0 0 0 1 ┘회전 변환 행렬
- 90˚ 회전에 대한 변환행렬(Rotation transformation matrix)을 설계하면 아래와 같다.
- 표준기저벡터 e1을 90˚ 회전한 벡터 : (0,1)
- 표준기저벡터 e2를 90˚ 회전한 벡터 : (-1,0)
- 90˚ 회전 변환을 수행하는 행렬은 다음과 같이 설계할 수 있음
R(90˚) = R(π/2) = ┌ 0 -1 ┐
└ 1 0 ┘- -90˚ 회전에 대한 변환행렬을 설계하면 아래와 같다.
- 표준기저벡터 e1을 90˚ 회전한 벡터 : (0, -1)
- 표준기저벡터 e2를 90˚ 회전한 벡터 : (1,0)
- -90˚ 회전 변환을 수행하는 행렬은 다음과 같이 설계할 수 있음
R(-90˚) = R(-π/2) = ┌ 0 1 ┐
└ -1 0 ┘- 각 θ로 벡터 공간을 회전시키는 회전 변환행렬을 설계하면 아래와 같다
- 표준기저벡터 e1을 θ만큼 회전한 벡터 : (cosθ, sinθ)
- 표준기저벡터 e2를 θ만큼 회전한 벡터 : (-sinθ, cosθ)
- θ 회전 변환을 수행하는 행렬은 다음과 같이 설계할 수 있음
R(θ) = ┌ cosθ -sinθ ┐
└ sinθ cosθ ┘- 행렬을 이용하면 x, y, z에서 벡터 라디안으로 회전시킬 수 있다.
- 회전축을 기준으로 시계 방향으로 회전한다.
회전 각도가 θ이고 x, y, z에서 회전하는 경우
┌ 1 0 0 0 ┐
| 0 cosθ sinθ 0 |
X(θ) = | 0 -sinθ cosθ 0 |
└ 0 0 0 1 ┘
┌ cosθ 0 -sinθ 0 ┐
| 0 1 0 0 |
Y(θ) = | sinθ 0 cosθ 0 |
└ 0 0 0 1 ┘
┌ cosθ sinθ 0 0 ┐
| -sinθ cosθ 0 0 |
Z(θ) = | 0 0 1 0 |
└ 0 0 0 1 ┘전단 변환 행렬
- 축의 방향으로 미든 변환을 전단 변환이라고 한다.
- 전단 변환 행렬(Shear transformation matrix)은 e1을 고정한 상태에서 e2를 x축 방향으로 미는 경우를 뜻한다.
- e1의 변환 결과 : (1,0)
- e2의 변환 결과 : (1,1)
S = ┌ 1 1 ┐
└ 0 1 ┘- 전단 변환에서 미는 크기는 1행 2열에 위치한 원소 값을 변경해 조절이 가능함
- x축으로 a만큼 밀게 된다면
S = ┌ 1 a ┐
└ 0 1 ┘삼각함수 덧셈 정리
// cos 함수와 sin 함수의 덧셈 정리
cos(α + β) = cosα cosβ - sinα sinβ
sin(α + β) = sinα cosβ + cosα sinβ
// 각 α에 대한 회전 변환
R_α = ┌ cosα -sinα ┐
└ sinα cosα ┘
// 각 β에 대한 회전 변환
R_β = ┌ cosβ -sinβ ┐
└ sinβ cosβ ┘
// 이 둘을 합한 각 α + β의 회전 변환
R_(α+β) = ┌ cos(α+β) -sin(α+β) ┐
└ sin(α+β) cos(α+β) ┘
// 각 α + β의 회전 변환은
// 각 α에 대한 회전 변환을 수행 후 각 β에 대한 회전 변환을 이어서 변환 결과와 동일
R_β · R_α = ┌ cosβ -sinβ ┐ ┌ cosα -sinα ┐
└ sinβ cosβ ┘ └ sinα cosα ┘
= ┌ cosα cosβ - sinα sinβ -(sinα cosβ + cosα sinβ) ┐
└ cosα sinβ + sinα cosβ cosα cosβ - sinα sinβ ┘
= ┌ cos(α+β) -sin(α+β) ┐
└ sin(α+β) cos(α+β) ┘
// 이 식으로 부터 삼각함수의 덧셈 정리 식을 얻을 수 있음역행렬
- 선형 변환을 수행하는 행렬은 본질적으로 함수의 성질을 지닌다.
- 그렇기에 항등함수와 역함수에 대응하는 행렬이 존재함
- 항등행렬(identity Matrix)은 원 공간의 변화없이 동일한 공간으로 유지하는 변환을 의미한다.
- 항등행렬은 단위행렬(Unit Matrix)이라고도 한다.
- 대각 행렬의 대각 요소가 모두 1인 행렬
- 항등행렬은 I로 표기한다.
- 역행렬(Inverse Matrix)은 역함수와 동일하게 위 첨자 ^-1을 사용한다.
I = ┌ 1 0 ┐
└ 0 1 ┘
A · A^-1 = A^-1 · A = I- 역행렬은 n x n 크기의 행렬 A가 있고, AB = BA = I 에서 n x n의 행렬 B가 존재한다면
- A 행렬을 가역행렬(invertible matrix)이라고 한다.
- 행렬 B는 n x n을 갖는 역행렬이라고 한다.
역행렬 판별 행렬
- 함수가 역함수를 갖기 위해선 전단사함수여야한다.
- 이와 동일하게 행렬도 두 공간의 변환이 전단사로 대응될 때만 역행렬이 존재함
- 어떤 행렬에 대해 역행렬이 존재하는지 파악할 수 있는 특별한 수식을 행렬식(Determinant)이라 한다.
- det() 의 기호로 표시한다.
A = ┌ a b ┐
└ c d ┘
det(A) = ad - bc- 행렬식 det(A)의 값이 0인 선형 변환은 전단사 대응이 성립하지 않아 역행렬이 존재하지 ㅇ낳는다.
- det(A)의 값은 두 표준기저벡터가 형성한 정사각형의 공간을 행렬 A를 사용해 변환한 공간의 넓이와 동일하다.
- 즉, det(A)는 A행렬을 통해 변환시킨 공간의 넓이와 동일함
크기 변환 행렬의 역행렬
- 변화된 크기만큼 거꾸로 크기를 변화시키는 방법으로 크기 변환행렬의 역행렬을 구할 수 있다.
//크기 변환행렬
S = ┌ a 0 ┐
└ 0 b ┘
S^-1 = ┌ 1/a 0 ┐
└ 0 1/b ┘- 역행렬을 통해 변화시킨 크기를 원래상태로 변경시킬 수 있음
전단 변환 행렬의 역행렬
- 원 공간에서 x축으로 a만큼 민 전단 변환행렬의 역행렬은 a의 반대수를 대입해 다음과 같이 구할 수 있다.
S = ┌ 1 a ┐
└ 0 1 ┘
S^-1 = ┌ 1 -a ┐
└ 0 1 ┘회전 변환 행렬의 역행렬
R_θ = ┌ cosθ -sinθ ┐
└ sinθ cosθ ┘
R_θ^-1 = ┌ cosθ sinθ ┐
└ -sinθ cosθ ┘행렬 곱의 역행렬
1. 합성함수에 해당하는 두 행렬 곱의 역행렬은 다음 수식을 성립함
(A · B)^-1 = B^-1 · A^-1
2. 역행렬이 존재하는 두 행렬 A와 B를 곱한 행렬 C가 있다면
A · B = C
C의 역행렬이 존재할 때 다음 식이 성립함
C · C^-1 = I
3. C에 행렬 A와 B를 대입해 풀어보면 다음과 같다.
(A · B) · (A · B)^-1 = I
4. 위 식의 양변에 A의 역행렬 A^-1을 곱하면 다음과 같이 전개된다.
A^-1 · (A · B) · (A · B)^-1 = A^-1
행렬의 곱은 결합법칙이 성립하므로 다음과 같이 전재할 수 있다.
(A^-1 · A) · B · (A · B)^-1 = A^-1
A^-1, A는 항등행렬이므로 위 식은 다음과 같이 간략화된다.
B · (A · B)^-1 = A^-1
양변에 B의 역행렬 B^-1을 곱해주면
B^-1 · B · (A · B)^-1 = B^-1 · A^-1
B^-1, B역시 항등행렬이므로 이를 소거하면 1번식이 성립함을 알 수 있다.
(A · B)^-1 = B^-1 · A^-1
출처
https://m.yes24.com/Goods/Detail/107025224
이득우의 게임 수학 - 예스24
39가지 실시간 렌더링 게임 프로그래밍 실습 예제를 하나씩 따라 해보며 독자가 직접 체득하는 흥미로운 게임 수학의 세계! 게임 개발자와 그래픽 아티스트들이 궁금해 했던 3D 가상 세계와 메타
m.yes24.com
https://wecandev.tistory.com/207
[이득우 게임수학] 5. 행렬: 가상 세계의 변환 도구
5.1 선형성: 예측 가능한 비례 관계 벡터와 스칼라 곱셈으로 생성된 벡터는 벡터와 평행한 원점을 지나는 일직선 상에 위치한다. 이러한 성질을 선형성(Linearity)이라고 한다. 선형성을 가법성(Addit
wecandev.tistory.com
https://erikanes.tistory.com/470
[게임수학] 벡터와 행렬 (3)
74. 행렬이란 무엇인가 75. 행렬의 합 및 스칼라 곱셈 76. 인접행렬 그래프 탐색으로 길을 찾을때 사용될 수 있다. 77. 행렬의 곱셈 위에서 작성한 그래프의 인접행렬을 제곱하면 두번 이동해서 도
erikanes.tistory.com
https://parksh86.tistory.com/132
[게임 수학] 행렬 - Matrix
행렬 - MATRIX 수학에서, 행렬(行列, matrix)은 수나 기호, 수식 등을 네모꼴로 배열한 것으로, 괄호로 묶어 표시한다. 3차원 이미지를 2차원 평면에 투영하거나 사실적인 움직임을 그려내기 위해서
parksh86.tistory.com
'게임수학' 카테고리의 다른 글
| [게임수학] 벡터의 내적 (0) | 2024.04.22 |
|---|---|
| [게임수학] 어파인 공간(Affine space) (0) | 2024.04.22 |
| [게임수학] 삼각함수 (0) | 2024.04.22 |
| [게임수학] 벡터 (0) | 2024.04.22 |
| [게임수학] 수 (0) | 2024.04.22 |
선형성?
- 벡터와 스칼라 곱으로 생성된 벡터는 벡터와 평행한 원점을 지나는 일직선 상에 위치한다.
- 이러한 성질을 선형성(Linearity)라고 한다.
- 수학에서는 선형성을 가법성(Additivity)과 1차 동차성(Homogeneity of degree1) 두 가지 조건을 모두 만족하는 함수의 성질로 정의한다.
f(x1 + x2) = f(x1) + f(x2) // 가법성
f(k · x) = k · f(x) //1차 동차성선형함수
- 원점을 지나는 직선 함수가 있다고 생각해보자
f(x) = ax
y = ax // 출력의 원소를 y로 표시 (직선 방정식)
// 선형성의 첫 번째 성질인 가법성 검증
// 좌변과 우변의 값이 동일한지 확인하는 것으로 판별 가능
f(x1 + x2) = a(x1 + x2) //좌변
f(x1) + f(x2) = ax1 + ax2 //우변
// 선형의 두 번째 성질인 1차 동차성 검증
// a, x, k가 모두 체의 성질을 가지는 실수인 경우
// 체는 곱셈에 대해 결합법칙과 교환법칙이 성립
f(kx) = a(kx) //좌변
kf(x) = k(ax) //우변- 위 식에서 증명했듯 y = ax는 선형성을 만족하는 것을 알 수 있다.
- f(x) = x^2와 같은 곡선의 함수도 선형성을 만족하는지 판별해보자
f(x1 + x2) = (x1 + x2)^2 = x1^2 + x2^2 + 2x1x2 //좌변
f(x1) + f(x2) = x1^2 + x2^2 //우변- 위 함수는 좌우변의 결과가 다르므로 선형성을 만족하지 않는다.
- f(x) = ax 에 스칼라 b를 더한 f(x) = ax + b는 선형성을 만족하는지 확인해보자
f(x1 + x2) = a(x1 + x2) + b //좌변
f(x1) + f(x2) = ax1 + ax2 + 2b //우변- 위 함수는 b만큼의 차이 때문에 가법성을 만족하지 않는다.
- 선형성이란 곧게 뻗은 직선의 성질을 뜻하는 것이 아니라, 두 집합의 순수한 비(Ratio)로 구성된 1차적 대응관계를 의미한다.
- 함수 f(x) = ax에서 대응되는 두 집합은 순수한 비로 구성되어 있기 때문에 다른 입력값을 투여했을 때 어떤 출력값이 나올지 쉽게 예측할 수 있음
- 반대로 역함수 f(x) = 1/a(x)를 사용하면 출력값으로부터 입력값을 거꾸로 계산하는 것이 가능함
벡터 공간의 선형 변환
- 정의역에 해당하는 벡터 공간을 V, 그 원소를 v로, 공역에 해당하는 벡터 공간을 W, 그 원소를 w로 표시하고 두 벡터 공간의 대응관계를 표현하면 다음과 같다.

- 입력에 사용한 2차원 벡터가 (x, y)로 구성되어 있는 경우, x와 y는 물과 기름과 같이 서로 독립된 관계를 형성한다.
- 선형성을 가지는 함수는 순수한 비의 형태로 구성되어 있다.
- x와 y 각각에 대해 선형성을 유지하고자 한다면 이들은 ax와 by 같은 단순 비의 형태를 사용할 것
- 이를 섞은 최종 결과는 각 비의 결과를 더한 ax + by의 형태가 될 것
- 따라서 2차원 벡터를 입출력으로 사용하는 선형성을 가지는 함수는 다음과 같이 설계될 것
f(V) = f(x, y) = (ax + by, cx + dy)- 위 함수가 가법성을 만족하는지 검증하면 아래와 같다.
//가법성 검증
f(v) = f(x,y) = (ax + by, cx + dy)
f(v1 + v2) = f(x1 + x2, y1 + y2)
= (a(x1 + x2) + b(y1 + y2), c(x1 + x2) + d(y1 + y2)) //좌변
f(v1) + f(v2) = (ax1 + by1, cx1 + dy1) + (ax2 + by2, cx2 + dy2)
= (ax1 + ax2 + by1 + by2, cx1 + cx2 + dy1 + dy2) //우변
∴ f(v1 + v2) = f(v1) + f(v2)
//1차 동차성 검증
kf(v) = (kax + kby, kcx + kdy) //좌변
f(kv) = (akx + bky, ckx + dky) //우변
∴ f(v1 + v2) = f(v1) + f(v2)- 함수 f(x, y)는 가법성과 1차 동차성을 만족하므로 선형함수다.
- 표준기저벡터의 선형 결합으로 형성된 벡터 공간은 선형성을 지닌다.
- 이 벡터 공간을 선형 함수로 변화시킨 새로운 공간도 기저벡터의 선형 결합으로 형성되므로 선형성을 지닌다.
- 두 공간이 동일한 구조를 지닐 때 두 공간의 대응 관계를 변환(Transformation)이라 한다.
- 아래처럼 선형성을 유지시켜주는 선형함수는 선형 변환(Linear transformation)이라고 한다.
- 벡터 공간에서 발생하는 선형 변환의 원리는 크기 변환이나 회전 변환과 관련이 있다.
- 임의의 벡터 V의 크기를 k배 늘리는 작업은 스칼라 곱셉으로 표현이 가능하다.
- f(V) = f(x, y) = (kx, ky)
- 이는 (ax + by, cx + dy) 형식에 a = k, b = 0, c = 0, d = k를 대입한 결과와 동일하므로 선형 변환이다.
- 임의의 벡터 V를 각θ 만큼 회전시키는 작업은 다음과 같은 함수로 표현이 가능
- f(V) = f(x, y) = (cosθ·x - sinθ·y, sinθ·x + cosθ·y)
- 이는 a = cosθ, b = -sinθ, c = sinθ, d = cosθ를 대입한 결과이므로 선형 변환이다.
- 벡터 공간에서의 선형변환은 단순 비례 관계로 구성된 선형 함수 f(x) = ax처럼 두 집합의 순수한 비를 통해 예측할 수 있는 형태로 변환된다.
- 역함수를 통해 변환 후의 벡터로부터 변환 전의 벡터를 파악할 수 있다.
- 선형 변환의 원리는 게임의 가상세계를 구축하는데 필요한 모든 변환의 기본 바탕이 된다.
- 선형 변환을 안정적이고 빠르게 계산할 수 있는 체계가 구축된다면 컴퓨터를 사용해 게임이 요구하는 가상 세계의 기반을 손쉽게 구축할 수 있음
- 선형 변환의 계산 과정을 체계화하여 손쉽게 계산할 수 있는 도구가 행렬이다.
행렬?
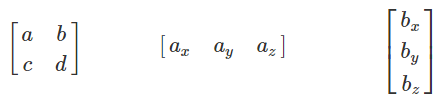
- 행렬(Matrix)은 수를 사각형의 형태로 행과 열을 맞춰 배열한 테이블이다.
- n개의 행과 m개의 열로 구성된 반듯한 사각형의 형태를 띤다.
- 행렬은 선형 변환과 벡터를 나타내는데 사용된다.
- 벡터는 한 줄로 구성된 행렬로 표현되며, 가로와 세로 두 가지 표현 방식이 존재한다.
- (x, y)로 구성된 2차원의 벡터는 A와 같이 열벡터로 표현되거나 B와 같이 행벡터로 표현될 수 있다.
A = ┌ x ┐ B = [ x y ]
└ y ┘- 선형 변환을 표현할 때는 행과 열의 크기가 같은 정방행렬(Square matric)을 사용한다.
- 2차원 벡터 공간의 선형 변환 f(x, y) = (ax + by, cx + dy)는 2 x 2크기의 정방행렬로 표현된다.
A = ┌ a b ┐
└ c d ┘- 정방행렬 A는 2개의 행벡터 또는 2개의 열벡터로 구성된다고 할 수 있다.
- 정방행렬 A를 행벡터와 열벡터로 분석하면
- 첫 번째 행벡터는 (a, b), 두 번째 행벡터는 (c, d)이다.
- 첫 번째 열벡터는 (a, c), 두 번째 열벡터는 (b, d)가 된다.
행렬의 기본 연산
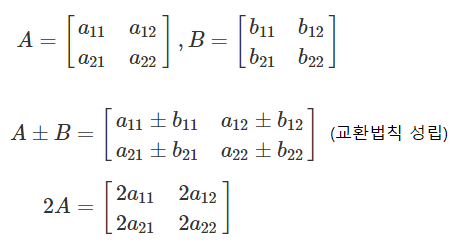
- 반드시 알아야 하는 행렬의 연산은 아래 4가지다.
- 행렬과 행렬의 덧셈
- 행렬과 스칼라의 곱셈
- 행렬의 전치(Transpose)
- 행렬과 행렬의 곱셈
//행렬과 행렬의 덧셈
A + B = ┌ a b ┐ + ┌ e f ┐ = ┌ a + e b + f ┐
└ c d ┘ └ g h ┘ └ c + g d + h ┘
//행렬과 스칼라의 곱셈
k · A = k · ┌ a b ┐ = ┌ k · a k · b ┐
└ c d ┘ └ k · c k · d ┘
//행렬의 전치
┌ a d ┐T
│ b e │ = ┌ a d c ┐
└ c f ┘ └ d e f ┘
//전치 행렬은 행과 열의 같은 번호끼리 교환하는 것행렬의 곱
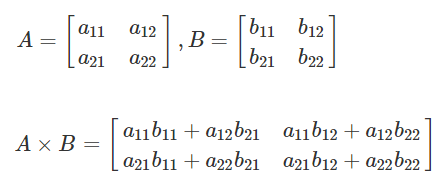
- 행렬의 곱셈은 앞에 위치한 행렬의 행벡터와 뒤에 위치한 행렬의 열벡터를 각각 곱하는 방식으로 진행된다.
- 행렬 곱셈의 중요한 성질 중 하나는 교환법칙이 성립하지 않는다는 점이다.
- 그러나 결합법칙은 만족한다.
- 행렬의 곱은 행렬의 내적과 같다.
//교환 법칙
A · B = ┌ a b ┐ · ┌ e f ┐ = ┌ ae + bg af + bh ┐
└ c d ┘ └ g h ┘ └ ce + dg cf + dh ┘
B · A = ┌ e f ┐ · ┌ a b ┐ = ┌ ae + cf be + df ┐
└ g h ┘ └ c d ┘ └ ag + ch bg + dh ┘
∴ A · B ≠ B · A
//결합 법칙
A · (B · C) = ┌ a b ┐ · ( ┌ e f ┐ · ┌ i j ┐ )
└ c d ┘ ( └ g h ┘ └ k l ┘ )
= ┌ a b ┐ · ┌ ei + fk ek + fl ┐
└ c d ┘ └ gi + hk gj + hl ┘
= ┌ aei + afk + bgi + bhk aej + afl + bgj + bhl ┐
└ cei + cfk + dgi + dhk cej + cfl + dgj + dhl ┘
(A · B) · C = ┌ a b ┐ · ( ┌ e f ┐ · ┌ i j ┐ )
└ c d ┘ ( └ g h ┘ └ k l ┘ )
= ┌ a b ┐ · ┌ ei + fk ek + fl ┐
└ c d ┘ └ gi + hk gj + hl ┘
= ┌ aei + afk + bgi + bhk aej + afl + bgj + bhl ┐
└ cei + cfk + dgi + dhk cej + cfl + dgj + dhl ┘
∴ (A · B) · C = A · (B · C)- 다른 특징 중 하나는 행렬 곱을 전치한 결과는 순서를 바꾼 후 각각 전치해 곱한 결과와 동일하다.
//중략
∴ (A · B)^T = B^T · A^T정방 행렬의 곱셈
- 2 x 2 정방행렬이 2차원 벡터 공간의 선형 변환에 대응된다면, 2 x 2 정방행렬 간의 곱은 합성함수에 대응되는 연산이다.
- 백터 v에 선형 변환을 나타내는 2 x 2 정방행렬 A, B를 순서대로 연산한다면, 수식은 아래와 같다.
- B · A · v

- 이는 위 그림과 같이 세 개의 2차원 벡터 공간 V, U, W에 대해 두 번의 선형 변환을 거쳐 벡터 공간 V에 속한 벡터 v가 벡터 공간 W의 벡터 w에 대응되는 관계로 해석할 수 있다.
- 선형 변환을 담당하는 정방행렬 A, B와 벡터 v의 각 요소는 다음과 같이 행렬로 나타낼 수 있다.
B = ┌ e f ┐
└ g h ┘
A = ┌ a b ┐
└ c d ┘
v = ┌ x ┐
└ y ┘- 벡터 v가 벡터 w로 변환되는 과정은 다음과 같은 행렬 곱으로 표현할 수 있다.
w = ┌ e f ┐ · ┌ a b ┐ · ┌ x ┐
└ g h ┘ └ c d ┘ └ y ┘- 합성함수는 결합법칙을 만족하기 때문에, 합성함수에 대응하는 행렬의 곱셈도 결합법칙을 만족한다.
- 따라서 행렬의 연산 순서를 바꾸어도 최종 계산된 벡터 w 값은 동일함
A · v = ┌ a b ┐ · ┌ x ┐ = ┌ ax + by ┐
└ c d ┘ └ y ┘ └ cx + dy ┘
// 1번 식
B·(A·v) = ┌ e f ┐ · ┌ ax + by ┐ = ┌ e(ax+by) + f(cx+dy) ┐
└ g h ┘ └ cx + dy ┘ └ g(ax+by) + h(cx+dy) ┘
B · A = ┌ e f ┐ · ┌ a b ┐ = ┌ ae+cf be+df ┐
└ g h ┘ └ c d ┘ └ ag+ch bg+dh ┘
// 2번 식
(B·A)·v = ┌ x(ae+cf) + y(be+df) ┐
└ x(ag+ch) + y(bg+dh) ┘- 1번 식과 2번 식은 동일한 값이므로 다음 식이 성립
w = B · (A · v) = (B · A) · v- 결합 법칙이 성립하는 행렬 곱의 성질은 컴퓨터 그래픽 연산에서 아주 유용하게 활용된다.
- 100개의 점으로 구성된 물체가 모니터에 표현되기 까지 5번의 선형 변환이 발생한다고 가정
- 물체의 점을 각각 v1, ..., v100으로 표기
- 선형 변환을 수행하는 행렬을 각각 A, B, C, D, E라고 하면
컴퓨터가 수행할 연산은 다음과 같다.
E · D · C · B · A · v1
...
E · D · C · B · A · v100- 각 점마다 5번의 행렬 곱이 수행되므로 100개 점에 대한 행렬 곱의 총 횟수는 500이 될 것
- 이때 결합 법칙이 성립하는 행렬 연산의 특징을 이용하면 계산량을 줄이되 동일한 결과를 얻을 수 있다.
- 행렬 곱을 4번 수행해서 합성함수에 해당하는 행렬 F를 미리 만든다.
- F = E · D · C · B · A
- 이제 각 점에 대해 미리 계산된 행렬 F만 곱하면 동일한 결과가 나온다.
컴퓨터가 수행할 연산은 다음과 같다.
F · v1
...
F · v100- 각 점에 대한 행렬 곱 횟수는 최초 합성 변환을 만들기 위한 4번의 행렬 곱과 벡터마다 1번의 행렬 곱이 수행되어 104가 된다.
- 정리하면 행렬은 컴퓨터 그래픽스에서 가상 세계를 구축하는데 필요한 계산량을 크게 줄여주는 역할을 함
행렬의 설계
- 평면상의 물체를 원하는 형태로 변환하기 위해 2 x 2 행렬을 설계하는 방법
- 벡터 공간 V를 구성하는 두 표준기저벡터 (1, 0)과 (0, 1)은 선형 변환을 통해 새로운 벡터 공간 W의 벡터 (a, b)와 (c, d)에 대응되어 변환된다면
- 벡터 공간 V의 벡터 v = (x, y)는 아래와 같은 표준기저 벡터의 선형 결합을 통해 생성된다.
v = (x,y) = x · (1,0) + y ·(0,1)
// 선형 변환
w = x(a,c) + y(b,d) = (ax + by, cx + dy)
// 이는 a, b, c, d로 만들어진 정방행렬에 벡터(x, y)를 곱한 결과와 동일
┌ a b ┐ · ┌ x ┐ = ┌ ax + by ┐
└ c d ┘ └ y ┘ └ cx + dy ┘- 위 정방행렬과 표준기저벡터가 변환된 두 벡터 (a, c)와 (b, d)와의 관계를 분석해보면 이들은 정방행렬을 구성하는 열벡터임을 알 수 있다.

- 벡터 공간 V의 (0, 0)에서 (1, 1)까지로 둘러싸인 사각형의 부분 공간은 선형 변환을 통해 부분 공간이 변환된다.
- 선형 변환을 통해 원하는 형태로 공간이 변화되도록 행렬을 스스로 설계할 수 있다.
인접 행렬

- 그래프 탐색으로 길을 찾을때 사용될 수 있다.
크기 변환 행렬
- 크기 변환행렬(Scale transformation matrix)은 물체의 크기를 변경하는 행렬이다.
- 크기 변환은 각 표준기저벡터를 동일한 방향으로 지정한 크기만큼 늘리는 변환을 의미한다.
- 이를 위해 (1,0)의 좌표를 갖는 e1과 (0,1)좌표를 갖는 e2의 두 표준기저벡터를 변환하면 아래와 같다.
a · (1,0) = (a,0)
b · (0,1) = (0,b)
S = ┌ a 0 ┐
└ 0 b ┘
// P = (x, y, z) 만큼 크기를 증가시키는 행렬
S = ┌ x 0 0 0 ┐
| 0 y 0 0 |
| 0 0 z 0 |
└ 0 0 0 1 ┘이동 행렬
- (x, y, z, 1) 벡터를 통해 이동 시킬 수 있다.
이동할 좌표가 P = (x, y, z)인 경우
// 일반적인 3D 공간에서의 이동 행렬
┌ 1 0 0 0 ┐
| 0 1 0 0 |
T = | 0 0 1 0 |
└ x y z 1 ┘
// 동차 좌표(Homogeneous Coordinates) 이동 행렬
┌ 1 0 0 x ┐
| 0 1 0 y |
T = | 0 0 1 z |
└ 0 0 0 1 ┘회전 변환 행렬
- 90˚ 회전에 대한 변환행렬(Rotation transformation matrix)을 설계하면 아래와 같다.
- 표준기저벡터 e1을 90˚ 회전한 벡터 : (0,1)
- 표준기저벡터 e2를 90˚ 회전한 벡터 : (-1,0)
- 90˚ 회전 변환을 수행하는 행렬은 다음과 같이 설계할 수 있음
R(90˚) = R(π/2) = ┌ 0 -1 ┐
└ 1 0 ┘- -90˚ 회전에 대한 변환행렬을 설계하면 아래와 같다.
- 표준기저벡터 e1을 90˚ 회전한 벡터 : (0, -1)
- 표준기저벡터 e2를 90˚ 회전한 벡터 : (1,0)
- -90˚ 회전 변환을 수행하는 행렬은 다음과 같이 설계할 수 있음
R(-90˚) = R(-π/2) = ┌ 0 1 ┐
└ -1 0 ┘- 각 θ로 벡터 공간을 회전시키는 회전 변환행렬을 설계하면 아래와 같다
- 표준기저벡터 e1을 θ만큼 회전한 벡터 : (cosθ, sinθ)
- 표준기저벡터 e2를 θ만큼 회전한 벡터 : (-sinθ, cosθ)
- θ 회전 변환을 수행하는 행렬은 다음과 같이 설계할 수 있음
R(θ) = ┌ cosθ -sinθ ┐
└ sinθ cosθ ┘- 행렬을 이용하면 x, y, z에서 벡터 라디안으로 회전시킬 수 있다.
- 회전축을 기준으로 시계 방향으로 회전한다.
회전 각도가 θ이고 x, y, z에서 회전하는 경우
┌ 1 0 0 0 ┐
| 0 cosθ sinθ 0 |
X(θ) = | 0 -sinθ cosθ 0 |
└ 0 0 0 1 ┘
┌ cosθ 0 -sinθ 0 ┐
| 0 1 0 0 |
Y(θ) = | sinθ 0 cosθ 0 |
└ 0 0 0 1 ┘
┌ cosθ sinθ 0 0 ┐
| -sinθ cosθ 0 0 |
Z(θ) = | 0 0 1 0 |
└ 0 0 0 1 ┘전단 변환 행렬
- 축의 방향으로 미든 변환을 전단 변환이라고 한다.
- 전단 변환 행렬(Shear transformation matrix)은 e1을 고정한 상태에서 e2를 x축 방향으로 미는 경우를 뜻한다.
- e1의 변환 결과 : (1,0)
- e2의 변환 결과 : (1,1)
S = ┌ 1 1 ┐
└ 0 1 ┘- 전단 변환에서 미는 크기는 1행 2열에 위치한 원소 값을 변경해 조절이 가능함
- x축으로 a만큼 밀게 된다면
S = ┌ 1 a ┐
└ 0 1 ┘삼각함수 덧셈 정리
// cos 함수와 sin 함수의 덧셈 정리
cos(α + β) = cosα cosβ - sinα sinβ
sin(α + β) = sinα cosβ + cosα sinβ
// 각 α에 대한 회전 변환
R_α = ┌ cosα -sinα ┐
└ sinα cosα ┘
// 각 β에 대한 회전 변환
R_β = ┌ cosβ -sinβ ┐
└ sinβ cosβ ┘
// 이 둘을 합한 각 α + β의 회전 변환
R_(α+β) = ┌ cos(α+β) -sin(α+β) ┐
└ sin(α+β) cos(α+β) ┘
// 각 α + β의 회전 변환은
// 각 α에 대한 회전 변환을 수행 후 각 β에 대한 회전 변환을 이어서 변환 결과와 동일
R_β · R_α = ┌ cosβ -sinβ ┐ ┌ cosα -sinα ┐
└ sinβ cosβ ┘ └ sinα cosα ┘
= ┌ cosα cosβ - sinα sinβ -(sinα cosβ + cosα sinβ) ┐
└ cosα sinβ + sinα cosβ cosα cosβ - sinα sinβ ┘
= ┌ cos(α+β) -sin(α+β) ┐
└ sin(α+β) cos(α+β) ┘
// 이 식으로 부터 삼각함수의 덧셈 정리 식을 얻을 수 있음역행렬
- 선형 변환을 수행하는 행렬은 본질적으로 함수의 성질을 지닌다.
- 그렇기에 항등함수와 역함수에 대응하는 행렬이 존재함
- 항등행렬(identity Matrix)은 원 공간의 변화없이 동일한 공간으로 유지하는 변환을 의미한다.
- 항등행렬은 단위행렬(Unit Matrix)이라고도 한다.
- 대각 행렬의 대각 요소가 모두 1인 행렬
- 항등행렬은 I로 표기한다.
- 역행렬(Inverse Matrix)은 역함수와 동일하게 위 첨자 ^-1을 사용한다.
I = ┌ 1 0 ┐
└ 0 1 ┘
A · A^-1 = A^-1 · A = I- 역행렬은 n x n 크기의 행렬 A가 있고, AB = BA = I 에서 n x n의 행렬 B가 존재한다면
- A 행렬을 가역행렬(invertible matrix)이라고 한다.
- 행렬 B는 n x n을 갖는 역행렬이라고 한다.
역행렬 판별 행렬
- 함수가 역함수를 갖기 위해선 전단사함수여야한다.
- 이와 동일하게 행렬도 두 공간의 변환이 전단사로 대응될 때만 역행렬이 존재함
- 어떤 행렬에 대해 역행렬이 존재하는지 파악할 수 있는 특별한 수식을 행렬식(Determinant)이라 한다.
- det() 의 기호로 표시한다.
A = ┌ a b ┐
└ c d ┘
det(A) = ad - bc- 행렬식 det(A)의 값이 0인 선형 변환은 전단사 대응이 성립하지 않아 역행렬이 존재하지 ㅇ낳는다.
- det(A)의 값은 두 표준기저벡터가 형성한 정사각형의 공간을 행렬 A를 사용해 변환한 공간의 넓이와 동일하다.
- 즉, det(A)는 A행렬을 통해 변환시킨 공간의 넓이와 동일함
크기 변환 행렬의 역행렬
- 변화된 크기만큼 거꾸로 크기를 변화시키는 방법으로 크기 변환행렬의 역행렬을 구할 수 있다.
//크기 변환행렬
S = ┌ a 0 ┐
└ 0 b ┘
S^-1 = ┌ 1/a 0 ┐
└ 0 1/b ┘- 역행렬을 통해 변화시킨 크기를 원래상태로 변경시킬 수 있음
전단 변환 행렬의 역행렬
- 원 공간에서 x축으로 a만큼 민 전단 변환행렬의 역행렬은 a의 반대수를 대입해 다음과 같이 구할 수 있다.
S = ┌ 1 a ┐
└ 0 1 ┘
S^-1 = ┌ 1 -a ┐
└ 0 1 ┘회전 변환 행렬의 역행렬
R_θ = ┌ cosθ -sinθ ┐
└ sinθ cosθ ┘
R_θ^-1 = ┌ cosθ sinθ ┐
└ -sinθ cosθ ┘행렬 곱의 역행렬
1. 합성함수에 해당하는 두 행렬 곱의 역행렬은 다음 수식을 성립함
(A · B)^-1 = B^-1 · A^-1
2. 역행렬이 존재하는 두 행렬 A와 B를 곱한 행렬 C가 있다면
A · B = C
C의 역행렬이 존재할 때 다음 식이 성립함
C · C^-1 = I
3. C에 행렬 A와 B를 대입해 풀어보면 다음과 같다.
(A · B) · (A · B)^-1 = I
4. 위 식의 양변에 A의 역행렬 A^-1을 곱하면 다음과 같이 전개된다.
A^-1 · (A · B) · (A · B)^-1 = A^-1
행렬의 곱은 결합법칙이 성립하므로 다음과 같이 전재할 수 있다.
(A^-1 · A) · B · (A · B)^-1 = A^-1
A^-1, A는 항등행렬이므로 위 식은 다음과 같이 간략화된다.
B · (A · B)^-1 = A^-1
양변에 B의 역행렬 B^-1을 곱해주면
B^-1 · B · (A · B)^-1 = B^-1 · A^-1
B^-1, B역시 항등행렬이므로 이를 소거하면 1번식이 성립함을 알 수 있다.
(A · B)^-1 = B^-1 · A^-1
출처
https://m.yes24.com/Goods/Detail/107025224
이득우의 게임 수학 - 예스24
39가지 실시간 렌더링 게임 프로그래밍 실습 예제를 하나씩 따라 해보며 독자가 직접 체득하는 흥미로운 게임 수학의 세계! 게임 개발자와 그래픽 아티스트들이 궁금해 했던 3D 가상 세계와 메타
m.yes24.com
https://wecandev.tistory.com/207
[이득우 게임수학] 5. 행렬: 가상 세계의 변환 도구
5.1 선형성: 예측 가능한 비례 관계 벡터와 스칼라 곱셈으로 생성된 벡터는 벡터와 평행한 원점을 지나는 일직선 상에 위치한다. 이러한 성질을 선형성(Linearity)이라고 한다. 선형성을 가법성(Addit
wecandev.tistory.com
https://erikanes.tistory.com/470
[게임수학] 벡터와 행렬 (3)
74. 행렬이란 무엇인가 75. 행렬의 합 및 스칼라 곱셈 76. 인접행렬 그래프 탐색으로 길을 찾을때 사용될 수 있다. 77. 행렬의 곱셈 위에서 작성한 그래프의 인접행렬을 제곱하면 두번 이동해서 도
erikanes.tistory.com
https://parksh86.tistory.com/132
[게임 수학] 행렬 - Matrix
행렬 - MATRIX 수학에서, 행렬(行列, matrix)은 수나 기호, 수식 등을 네모꼴로 배열한 것으로, 괄호로 묶어 표시한다. 3차원 이미지를 2차원 평면에 투영하거나 사실적인 움직임을 그려내기 위해서
parksh86.tistory.com
'게임수학' 카테고리의 다른 글
| [게임수학] 벡터의 내적 (0) | 2024.04.22 |
|---|---|
| [게임수학] 어파인 공간(Affine space) (0) | 2024.04.22 |
| [게임수학] 삼각함수 (0) | 2024.04.22 |
| [게임수학] 벡터 (0) | 2024.04.22 |
| [게임수학] 수 (0) | 2024.04.22 |
