벡터?
- 벡터(Vector)란 평면에서 시각적으로 의미 있는 물체를 생성하기 위해 평면을 구성하는 원소이다.
- 벡터는 크기와 방향을 가진 양을 나타내는 수학적 개념
데카르트 좌표계
- 데카르트 좌표계(Certesian coordination syste)는 직선의 수 집합을 수직으로 배치하여 평면을 표기하는 방식을 의미한다.
- 곱집합의 원어가 데카르트 곱(Certesian pruduct)임을 생각한다면 같은 의미임을 알 수 있다.

- 데카르트 좌표계는 위 그림과 같이 수평으로 배치한 첫 번째 실수 집합의 미지수를 x, 수직으로 배치한 두 번째 실수 집합의 미지수를 y로 표기함
- 원점을 기준으로 x축의 오른편, y축의 위편은 양의 영역을 나타낸다.
- 가로축 X와 세로축 Y를 통해 평면을 가르면 총 4개의 분면으로 나뉘는데 오른쪽 상단부터 반시계방향으로 순서를 붙인다.
- 1사분면, 2사분면, 3사분면, 4사분면
- 데카르트 좌표계의 한 원소는 곱집합과 동일하게 순서쌍으로 표현하며 좌표(Coordinate)라고 부른다.
- (x,y)
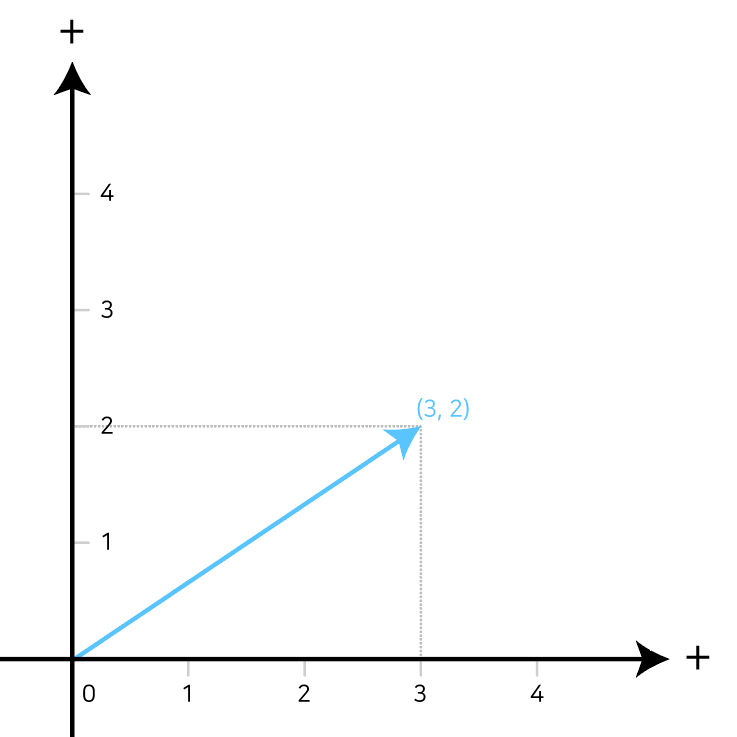
- 일반적으로 좌표는 수와 동일하게 위 그림과 같이 점 또는 원점으로부터의 화살표로 표현한다.
벡터 공간과 벡터
스칼라와 벡터
- 두 개 이상의 실수를 곱 집합으로 묶어 형성된 집합을 벡터 공간(Vector Space)이라고 한다.
- 벡터 공간의 원소를 벡터(Vector)라고 한다.
- 좌표값으로 사용하는 x와 y를 실수로 규정하기보단 체의 구조를 가지는 집합, 즉 체집합의 원소를 규정한다.
- 체의 구조를 가지는 수 집합의 원소를 스칼라(Scalar)라고 부른다
- 스칼라는 크기만을 가지고 방향이 없는 양을 의미
- 벡터와 반대되는 개념으로 단순히 크기만을 가진다.
- 벡터 공간을 표기할 때에는 대문자 V를 사용하고 이의 원소인 벡터는 소문자 v로 표기한다.
벡터 공간의 연산
- 벡터와 벡터의 덧셈(벡터의 합)
v1 + v2 = (x1, y1) + (x2, y2) = (x1 + x2, y1 + y2)- 벡터와 벡터의 뺄셈(벡터의 차)
V1 - V2 = (x1, y1) - (x2, y2) = (x1 - x2, y1 - y2)- 스칼라와 벡터의 곱셈(스칼라 곱)
a · v = a · (x, y) = (a · x, a · y)벡터 공간의 공리
- 벡터의 합
- 결합법칙 : u + (v + w) = (u + v) + w
- 교환법칙 : u + v = v + u
- 항등원 : v + 0 = v
- 역원 : v + (-v) = 0
- 스칼라 곱셈
- 호완성 : a(bv) = (ab)v
- 항등원 : 1 · v = v
- 벡터의 합에 대한 분배법칙 : a(u + v) = au + av
- 스칼라 곱셈에 대한 분배법칙 : (a + b)v = av + bv
- 벡터 공간의 공리는 모두 체의 공리를 기반으로 하기 때문에 해당 공리가 참임을 파악할 수 있다.
- 벡터의 합이 교환법칙을 만족하는 까닭은 두 스칼라의 덧셈이 교환법칙을 만족하기 때문
V1 + V2 = (x1, y1) + (x2, y2) = (x1 + x2, y1 + y2)
V2 + V1 = (x2, y2) + (x1, y1) = (x2 + x1, y2 + y1)
∴ V1 + V2 = V2 + V1
- 벡터 공간에서 합 연산을 적용하면 점의 움직임은 평면의 점을 각 축에 대해 독립적으로 평행 시동 시키는 작업이 된다.
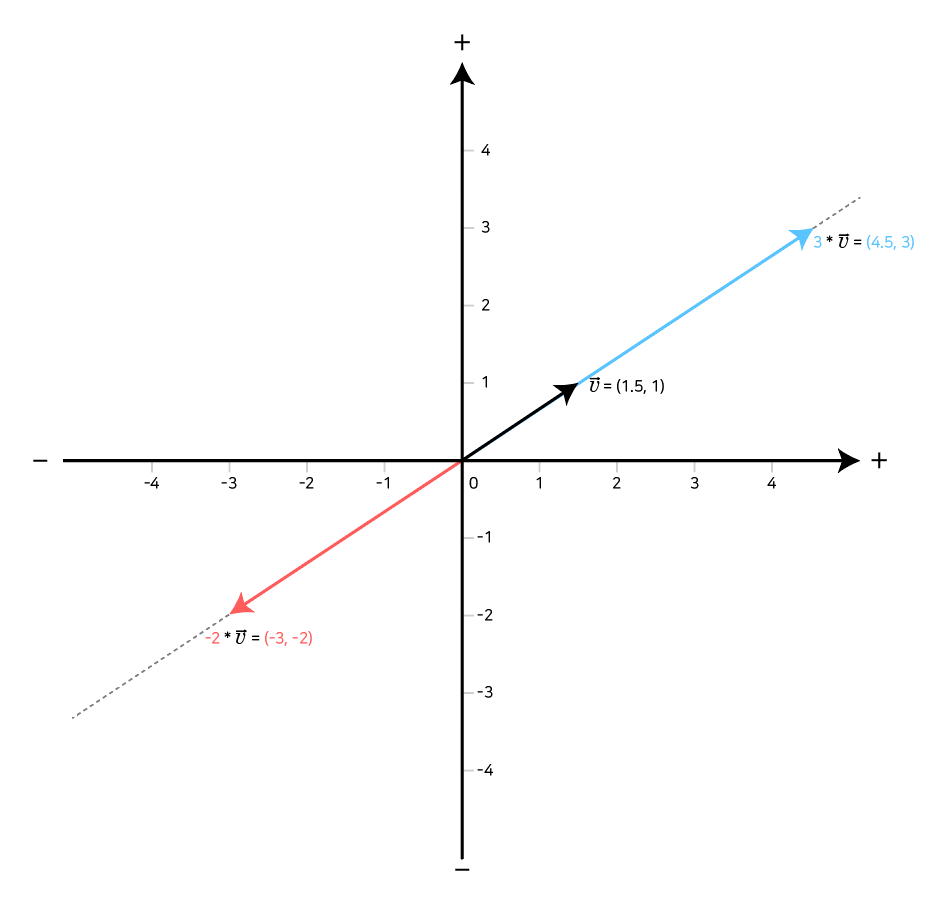
- 스칼라 곱셈으로 생성된 벡터는 원점을 지나고 벡터와 평행한 직선상에 위치한다.
- 스칼라 곱셈의 결과는 붉은색으로 표현한, 원점을 지나는 직선상의 벡터를 만들어낸다.
벡터의 크기
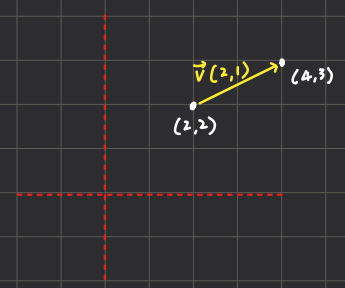
- 수의 크기는 절댓값 기호(||)를 사용해 구할 수 있다.
- 피타고라스 정리를 사용해 거리를 측정한다.

c^2 = a^2 + b^2
c = sqrt((a*a) + (b*b))
- 벡터의 크기는 노름(Norm)이라는 용어로 부르기도 한다.
- 임의의 벡터 v를 크기가 1인 단위벡터(Unit Vector)로 다듬는 작업을 정규화한다(Normalize)고 부른다.
- 벡터의 크기가 1이 되면 방향은 유지한 채 크기를 표준화할 수 있다.
norm(V) = V / |V|벡터의 결합과 생성
- 벡터 공간의 벡터의 합과 스칼라 곱셈 연산은 선형성이 있어 선형 연산이라고도 한다.
- 선형 연산을 사용해 n개의 스칼라와 n개의 벡터를 결합해 새로운 벡터 v 를 생성하는 수식을 선형 결합(Linear combination)이라고 한다.
a1·V1 + a2·V2 + a3·V3 + ... + an·Vn = V'- 벡터를 곱하는 모든 스칼라 값이 0이면 선형 결합의 결과는 항상 영벡터(Zero Vector)가 된다.
a1·V1 + a2·V2 + a3·V3 + ... + an·Vn = 0- 벡터에 곱하는 모든 스칼라 값이 0이면 선형 결합의 결과는 항상 영벡터가 된다.
- 그런데 0이 아닌 경우에도 영벡터는 나올수 있다. 그러한 경우를 선형 종속의 관계를 가진다고 표현한다.
2·(1, 1) + (-1)·(2, 2) = (0, 0)- 반면에 영벡터가 나오기 위해 모든 a값이 0 이어야 한다면 사용된 벡터들은 서로 선형 독립의 관계를 가진다고 표현한다.
0·(1, 2) + 0·(2, 1) = (0, 0)- 벡터 간의 선형적 관계는 벡터 공간을 다룰 때 중요하게 사용된다.
- 선형 독립의 관계를 가지는 벡터를 선형 결합하면 벡터 공간에 속한 모든 벡터를 생성할 수 있음

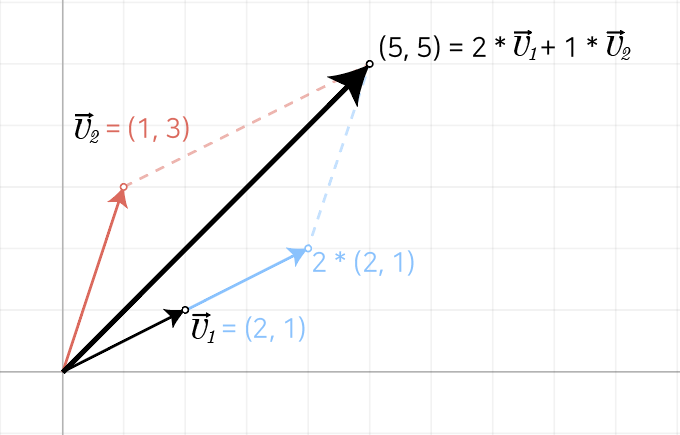
2차원 평면의 예제를 통해 백터 공간의 모든 벡터 생성하는지 살펴보기
두 벡터 U, V와 두 스칼라 a, b를 결합해 새로운 벡터 W를 생성하는 수식
W = a·U + b·V
두 벡터 U와 V가 선형 독립의 관계를 가진다면
위 선형 결합식으로 2차원 벡터 공간에 속한 모든 벡터를 생성할 수 있음
벡터 W = (5, 5)인 경우
(5, 5) = 5·(1, 0) + 5·(0, 1)
(5, 5) = 2·(2, 1) + 1·(1, 3)- 위 예제에서 제시한 (2, 1), (1, 3)을 결합했을 때 (5, 5)가 아닌 다른 벡터로 생성할 수 있음
순서쌍 (Wx, Wy)로 구성된 임의의 벡터 W를 생성하는 수식
(Wx, Wy) = a·(2, 1) + b·(1, 3)
x값과 y값을 분리해 식을 전개
2a + b = Wx
a + 3b + Wy
두 식을 a와 b에 대한 연립 방정식으로 풀어보면
그 값은 벡터 W의 좌표 값에 따라 결정되며 언제나 해가 존재함
a = (3Wx - Wy) / 5
b = (2Wy - Wx) / 5
따라서 벡터 (2, 1)과 벡터 (1,3)을 결합해
평면에 속한 모든 벡터를 생성할 수 있음
벡터 W값이 영벡터가 되는 a와 b의 해는 모두 0인 경우뿐
a = (3·0 - 0) / 5
b = (2·0 - 0) / 5- 위 식에서 벡터 (2, 1)과 (1, 3)은 서로 선형 독립의 관계를 가진다.
- 다른 두 벡터 (1, 2)와 (2, 4)를 결합할 경우
(5, 5) = a·(1, 2) + b·(2, 4)
a와 b를 연립방정식으로 보면
a + 2b = 5
2a + 4b = 5
이를 만족하는 a와 b는 구할 수 없다
2a + 4b = 10
2a + 4b = 5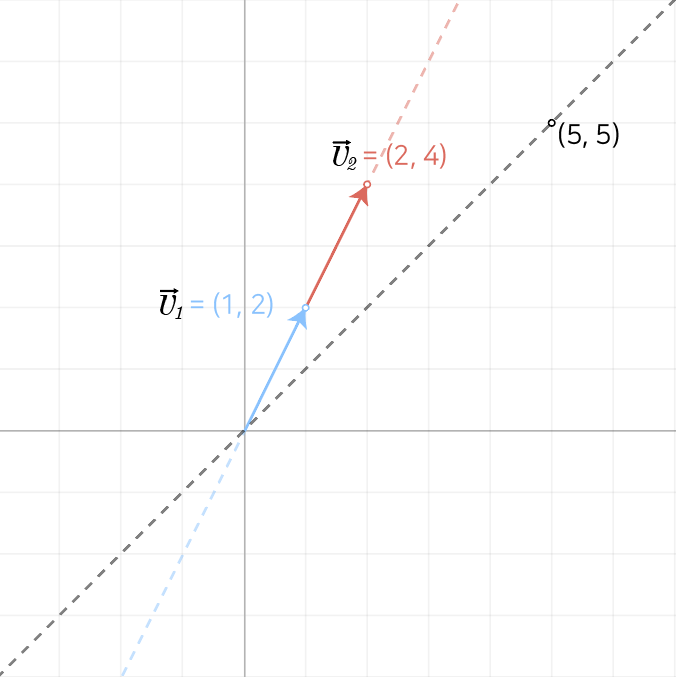
- 두 벡터 (1, 2)와 (2, 4)는 평행하지만 (5, 5)와는 서로 평행하지 않다.
- 평행한 두 벡터를 결합한 결과는 두 개의 벡터 결합이 아닌 하나의 벡터 (1, 2)에 스칼라 곱을 적용한 결과에 불과함
(x, y) = a·(1, 2) + b·(2, 4)
= a·(1, 2) + 2b·(1, 2)
= (a + 2b)·(1, 2)- 따라서 a와 b에 어떤 스칼라 값을 대입하더라도 선형 결합의 결과는 벡터 (1, 2)와 평핸한 벡터만 생성된다.
- (1, 2)와 (2, 5)의 관계를 선형 결합식으로 나타내면 아래와 같다.
2·(1, 2) + (-1)·(2, 4) = (0, 0)- 0이 아닌 임의의 계수 a와 b를 사용해 영벡터를 만들 수 있으므로 두 벡터는 선형 종속의 관계를 가진다.
- 벡터 3개의 선형 결합
평행하지 않은 두 벡터를 결합하면 평면의 모든 벡터를 만들 수 있음
만약 3개의 벡터를 사용한다면? 선형 종속과 선형 독립의 관점에서 분석하기
두 벡터 (2, 1)과 (1, 3)은 선형 독립의 관계를 가짐
0·(2, 1) + 0·(1, 3) = (0, 0)
선형 독립인 두 벡터에 스칼라 a와 b를 곱하고
새로운 스칼라 c와 임의의 벡터 (x, y)를 추가해
세개의 벡터로 구성된 선형 결합식을 만들면
a·(2, 1) + b·(1, 3) + c·(x, y) = (0, 0)- 세 벡터가 모두 선형 독립의 관계를 가지려면 위 식을 만족하는 모든 스칼라 a, b, c의 값은 0이 되어야 한다.
- 선형 독립인 두 벡터 (2, 1)과 (1, 3)을 결합해 평면의 모든 벡터를 생성할 수 있었음
- 따라서 두 벡터를 결합해 임의의 벡터 (x, y)에 -c를 곱한 -c·(x, y)를 생성할 수 있을 것
- 0이 아닌 스칼라 c를 사용해 영벡터를 만들 수 있으므로 선형 독립의 관계를 더 이상 만족하지 못함
-c·(x, y) + c·(x, y) = (0, 0)- 선형 독립의 관계가 유지되려면 2개의 벡터만 사용되어야 함
기저
- 벡터 공간 내 모든 백터를 생성할 수 있는 선형 독립 관계를 가지는 벡터의 집합을 기저(Basis)라고 한다.
- 집합의 개념인 기저에 속한 원소를 기저벡터(Basis vector)라고 한다.
- 벡터 (2, 1)은 기저 B = {(2, 1), (1, 3)}에 속한 기저벡터다.
- 기저벡터를 다른 값으로 변경하면 기저벡터로부터 세워진 벡터 공간의 모든 원소가 바뀐다.
- 이는 선형 변환의 기본 원리가 된다.
- 기저의 개념은 차원(Dimension)이라는 새로운 용어를 정의하는데 사용된다.
- 평면으로 구성된 벡터 공간을 생성하기 위한 기저는 수많은 경우의 수가 존재함
- 단, 기저 집합의 원소 수는 언제나 2개뿐이다.
- 따라서 명확한 정의에 의해 평면에 대응하는 벡터 공간을 비로소 2차원으로 정의할 수 있게 되었음
- 위에서 설명한 벡터 공간은 두 개의 실수 집합을 결합해 생성한 벡터 공간
- 수 집합의 기호와 차원의 정보를 첨자로 결합해 R^2로 나타낼 수 있음
- 이를 2차원 실벡터 공간(Real vector space)라고 함
- 한 축만 사용하는 단위 벡터 (1,0) , (0,1) 로 구성된 집합을 표준기저(Standard basis)라고 하며 기저의 각 원소를 표준기저벡터(Standard basis vector)라고 한다.
표준 기저 벡터는 순서대로 e1, e2로 표기
e1 = (1, 0)
e2 = (0, 1)- 벡터 공간의 차원에는 제약이 없기 때문에 R^3, R^4, ..., R^n으로 무한 확장이 가능함
- 3차원 벡터 공간의 표준기저는 늘어난 차원만큼 다음과 같이 구성된다.
e1 = (1, 0, 0)
e2 = (0, 1, 0)
e3 = (0, 0, 1)게임에서의 벡터
- 게임 개발에서 벡터는 다양한 용도로 활용되며, 주로 위치, 방향, 속도 등을 나타내기 위해 사용한다.
- 위치 표현
- 게임 오브젝트의 위치를 나타내기 위해 벡터가 사용된다.
- 위치 벡터는 해당 오브젝트가 어디에 위치하는지 정확히 표현한다.
- 이동 및 속도
- 오브젝트의 이동을 처리할 때 (보통 속도 * 방향 벡터)를 사용한다.
- 카메라 및 시야 관리
- 플레이어의 시점을 나타내거나, 카메라의 위치 및 방향을 제어할 때 벡터가 사용된다.
- 또한, 카메라가 향하는 방향을 나타내는 시야 벡터로서도 사용된다.
출처
https://m.yes24.com/Goods/Detail/107025224
이득우의 게임 수학 - 예스24
39가지 실시간 렌더링 게임 프로그래밍 실습 예제를 하나씩 따라 해보며 독자가 직접 체득하는 흥미로운 게임 수학의 세계! 게임 개발자와 그래픽 아티스트들이 궁금해 했던 3D 가상 세계와 메타
m.yes24.com
https://wecandev.tistory.com/204
[이득우 게임수학] 3. 벡터 : 가상 공간의 탄생
벡터(Vector)란 평면에서 시각적으로 의미 있는 물체를 생성하기 위해 평면을 구성하는 원소이다. 3.1 데카르트 좌표계 데카르트 좌표계(Cartesian coordinate syste)는 직선의 수 집합을 수직으로 배치하
wecandev.tistory.com
https://velog.io/@apth1023/%EA%B2%8C%EC%9E%84-%EC%88%98%ED%95%99-%EB%B2%A1%ED%84%B0
[게임 수학] 벡터
벡터의 기본 개념과 이를 응용한 실습(UE_Blueprint)을 진행해보도록 하겠습니다.
velog.io
https://walll4542developer.github.io/math/Cartesian-coordinate-system/
게임 수학 입문 03 - 데카르트 좌표계(Cartesian coordinate system)
실수와 실수의 곱집합을 사용하여 직선으로 표현되는 영역을 평면으로 확장해 표현할 수 있었습니다. 이렇게 직선의 수 집합을 수직으로 배치해 평면을 표기하는 방식을 데카르트 좌표계(Cartesi
walll4542developer.github.io
https://walll4542developer.github.io/math/Vector-Combination/
게임 수학 입문 04 - 벡터의 결합과 생성(Vector Combination)
벡터 공간의 기본 연산을 사용해 벡터를 움직이는 방법에 대해서 알아봤습니다. 이번에는 벡터의 기본 연산을 사용해 벡터 공간의 구조를 분석하고 이로부터 벡터 공간이 가진 다양한 성질을
walll4542developer.github.io
'게임수학' 카테고리의 다른 글
| [게임수학] 벡터의 내적 (0) | 2024.04.22 |
|---|---|
| [게임수학] 어파인 공간(Affine space) (0) | 2024.04.22 |
| [게임수학] 행렬 (1) | 2024.04.22 |
| [게임수학] 삼각함수 (0) | 2024.04.22 |
| [게임수학] 수 (0) | 2024.04.22 |
