3차원 공간
- 3차원 공간을 설계하는 방법은 왼손 좌표계와 오른손 좌표계 크게 두가지로 구분된다.
- 왼손 좌표계는 내가 바라보는 정면이 +z축 이고 위가 +y, 오른쪽이 +x인 방향이다.
- 오른손 좌표계는 나한테 오는 방향(나의 뒤방향)이 +z 축이고, 위가 +y, 오른쪽이 +x인 방향이다.
- 왼손과 오른손은 z축의 방향차이로 확인할 수 있다.
왼손 좌표계
- 왼손 좌표계의 대표적인 예는 Unity 게임 엔진이다.
- 왼손 좌표계를 사용하면 UX 측면에서 큰 이점이 생긴다.
- 3D상에서 2D를 표현할 때 Z축 값을 사용해 레이어 구분이 필요할 때가 있다.
- 이때 왼손 좌표계를 사용하면 화면에서 멀어질수록 Z축 값이 올라간다.
- Z축의 값과 오브젝트의 레이어 순서는 서로 비슷하기 때문에 구분이 가능하다.
- Y-UP를 사용하는 이유
- 다이렉트 X와 OpenGL은 Y-UP을 사용한다.
- Unreal Engine이나 Unity가 널리 사용되기 전에는 다이렉트 X와 OpenGL을 많이 사용함
- 익숙한 좌표계 사용을 위해 상용 엔진도 이 방식을 사용
오른손 좌표계
- 오른손 좌표계를 사용하는 대표적인 예는 블랜더이다.
- 대부분 수학에서 2D의 데카르트 좌표계에서 3D 좌표계로 넘어갈 때 오른손 좌표계를 사용함
- Z-UP을 사용하는 이유
- 공학적인 접근방식에서 Z-UP이 거의 표준처럼 사용
3차원 공간의 트랜스폼
- 3차원 트랜스폼 체계는 2차원 공간의 트랜스폼에서 기저벡트가 하나더 증가했을 뿐이다.
- 이동 변환을 위해 한 차원 더 늘어난 4차원 공간을 사용한다.
이동변환 행렬과 크기변환 행렬
- 이동변환은 Identity Matrix를 기반으로 축만 변경된다.
- 한 축이 변경되면 다른 축은 변경되지 않는다.
- 크기변환은 Identity Matrix 범위 내에서 변경된다.
- 이동변환과 크기변환은 차원마다 행렬식이 추가되기만하면 된다.
┌ S_x 0 0 0 ┐
S = │ 0 S_y 0 0 │
│ 0 0 S_z 0 │
└ 0 0 0 1 ┘
┌ 1 0 0 t_x ┐
T = │ 0 1 0 t_y │
│ 0 0 1 t_z │
└ 0 0 0 1 ┘표준기저벡터의 변화를 사용한 회전변환 행렬
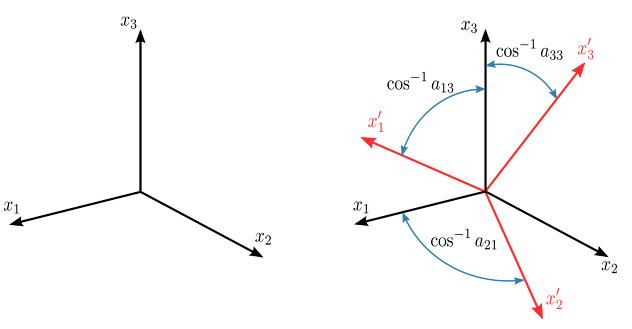
- 회전은 하나의 축을 변경하면 대부분의 축이 변경된다.
- 차원이 높아질 수록 해당 축의 회전은 더욱 넓은 범위의 축들을 변경하게 된다.
- 2D 공간의 회전(Z축 회전)은 x, y축만 영향을 끼침
- 3D 공간의 회전(X, Y축 회전) z축에도 영향을 끼침
표준기저벡터 X', Y', Z'(위 그림에서의 x'1, x'2, x'3) 값은
X'(x'1) = (X'x, X'y, X'z)
Y'(x'2) = (Y'x, Y'y, Y'z)
Z'(x'3) = (Z'x, Z'y, Z'z)
아래와 같은 식으로 적용할 수 있다.
┌ X'x Y'x Z'x 0 ┐
R = │ X'y Y'y Z'y 0 │
│ X'z Y'z Z'z 0 │
└ 0 0 0 1 ┘- 이 방법으로 3차원 공간의 회전을 지정한다는 것은 매번 3개의 변화된 표준기저벡터 값을 계산해야한다.
- 회전을 지정할 때는 일반적으로 회전하는 중심축과 각으로 표현된 회전량을 지정하는 방식을 사용한다,
- 2차원 공간은 하나의 평면만 존재하기 때문에 각으로 회전량을 지정하면 원하는 회전을 설계할 수 있다.
- 하지만 3차원 공간은 무수히 많은 평면으로 구성되기 때문에 새로운 방식이 필요하다.
오일러 각
- 오일러 각(Euler's angle)은 3차원 공간에서 물체가 놓인 방향을 3개의 각을 사용해 표시하는 방법이다.
- 한눈에 알아보기 쉽고 앞서 배웠던 회전 행렬로 적용이 용이한 엄청난 개념이 있는 덕분에 회전을 쉽게 적용할 수 있다.
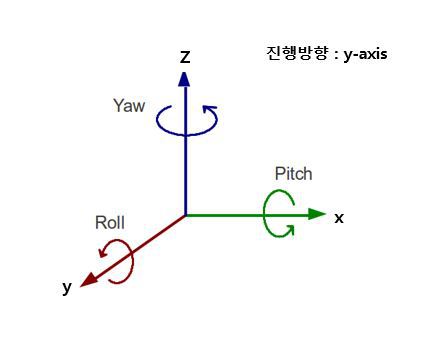
- 표준기저벡터를 축으로 하는 회전의 움직임은 방향에 따라 요(Yaw), 롤(Roll), 피치(Pitch)로 불린다.
- 3축의 회전 행렬은 다음과 같이 설계할 수 있다.
┌ 1 0 0 ┐
R_x = │ 0 cosθ -sinθ │
└ 0 sinθ cosθ ┘
┌ cosθ 0 sinθ ┐
R_y = │ 0 1 0 │
└ -sinθ 0 cosθ ┘
┌ cosθ -sinθ 0 ┐
R_z = │ sinθ cosθ 0 │
└ 0 0 1 ┘- 주의 깊에 살펴볼 부분은 y축의 회전행렬 R_y다.
- 다른 행렬은 모두 우측상단의 sin 함수가 음의 부호인 반면 R_y는 좌측 하단의 sin 함수가 음의 부호를 가진다.
- 3차원 공간에서는 x -> y -> z -> x -> y의 순서로 세 축이 순환하기 때문에 y축이 직교하는 평면은 xz 평면이 아니라 zx 평면이다.
회전 행렬 유도
- 세 번의 연속적인 회전으로 총 6가지 경우가 발생한다.
- x -> y -> z
- x -> z -> y
- y -> x -> z
- y -> z -> x
- z -> x -> y
- z -> y -> x
- 이중 5번째 순서에 대해 알아본다면
R = R_yaw · R_pitch · R_roll
┌ cosα cosy + sinα sinβ sinγ -cosα sinγ + sinα sinβ cosγ sinα cosβ ┐
R_α · R_β · R_γ = │ cosβ sinγ cosβ cosγ -sinβ │
└ -sinα cosγ + cosα sinβ sinγ sinα sinγ + cosα sinβ cosγ cosα cosβ ┘- 계산된 회전행렬의 열벡터는 표준기저벡터가 회전 변환된 로컬 축을 의미한다.
- 따라서 오일러 각으로 변화된 각 로컬 축 값은 다음과 같이 계산해 얻을 수 있다.
x_local = (cosα·cosy + sinα·sinβ·sinγ, cosβ·sinγ, -sinα·cosγ + cosα·sinβ·sinγ)
y_local = (-cosα·siny + sinα·sinβ·cosγ, cosβ·cosγ, sinα·sinγ + cosα·sinβ·sinγ)
z_local = (sinα·cosβ, -sinβ, cosα·cosβ)- 3차원 공간의 트랜스폼도 회전 변환이 발생할 때마다 로컬 축 데이터를 갱신하면 게임 로직에서 유용하게 사용할 수 있을 뿐만 아니라, 렌더링 로직에 필요한 회전행렬도 바로 만들어 낼 수 있다.
- 계산식으로 얻어낸 로컬 축 벡터를 각각 X = (X_x, X_y, X_z), Y = (Y_x, Y_y, Y_z), Z = (Z_x, Z_y, Z_z)로 지정하고, 이들을 열벡터로 꽃아넣어 얻어지는 3차원 공간의 회전행렬 R은 다음과 같다.
┌ X_x Y_x Z_x 0 ┐
R = │ X_y Y_y Z_y 0 │
│ X_z Y_z Z_z 0 │
└ 0 0 0 1 ┘3차원 모델링 행렬
- 3차원 공간의 트랜스폼을 구성하는 크기(S), 회전(R), 이동(T) 변환 행렬은 다음과 같다.
┌ S_x 0 0 0 ┐
S = │ 0 S_y 0 0 │
│ 0 0 S_z 0 │
└ 0 0 0 1 ┘
┌ X_x Y_x Z_x 0 ┐
R = │ X_y Y_y Z_y 0 │
│ X_z Y_z Z_z 0 │
└ 0 0 0 1 ┘
┌ 1 0 0 t_x ┐
T = │ 0 1 0 t_y │
│ 0 0 1 t_z │
└ 0 0 0 1 ┘
3개의 행렬을 TRS연산 순서에 따라 곱해 만든 모델링 행렬 M은 다음과 같다.
┌ X_x S_x Y_x S_y Z_x S_z t_x ┐
M = T · R · S = │ X_y S_x Y_y S_y Z_y S_z t_y │
│ X_z S_x Y_z S_y Z_z S_z t_z │
└ 0 0 0 1 ┘카메라 공간
- 월드에서의 좌표가 어떻든 카메라 관점에서 봤을 때 카메라는 세상의 좌표와 다르게 반대로 바라보는 모습이 될것
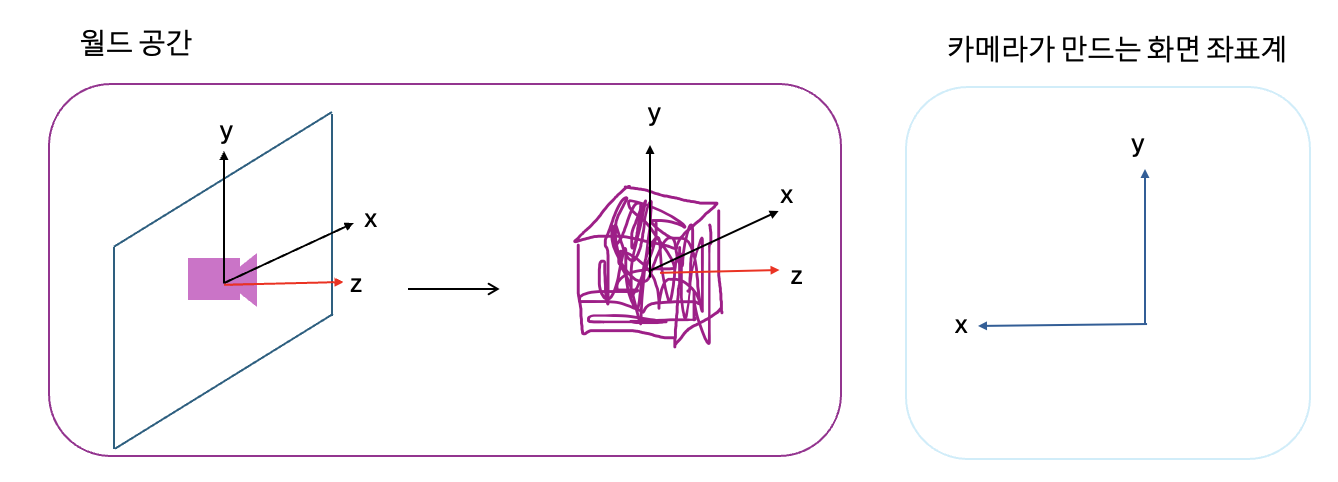
- 서로 반대되는 좌표계로 인해 와 값이 예상과 다르게 반대로 뒤집힐 것
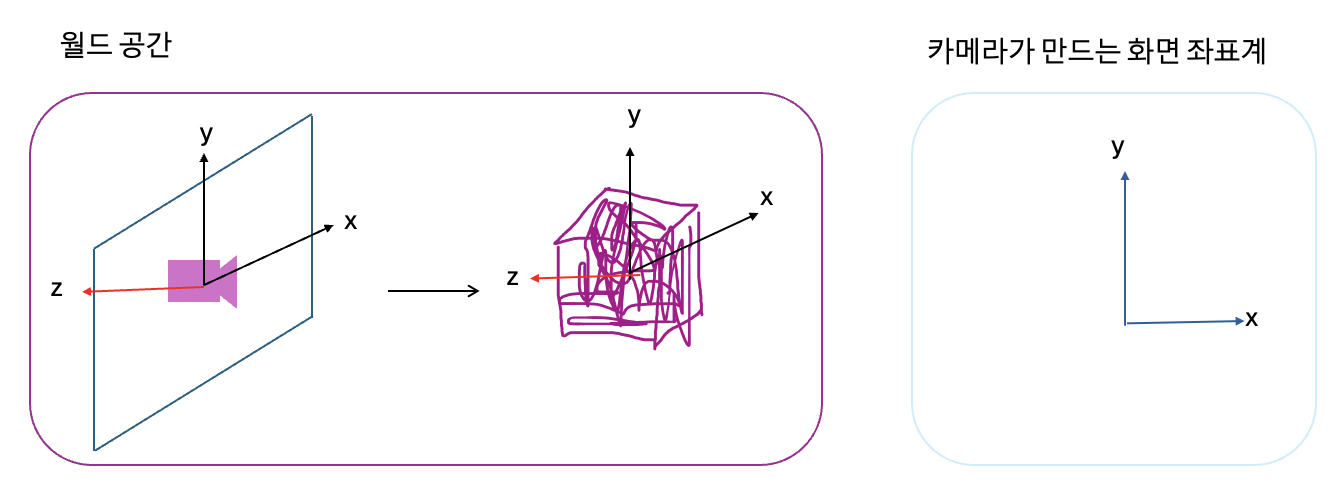
- 원래 좌표계를 사용하고자 한다면 카메라를 회전시켜서 축이 카메라 뒤편을 향하게 하면 우리가 원하는 좌표계로 물체가 나타날 것이다.
- 카메라는 크기의 개념이 없기 때문에, 카메라의 트랜스폼은 크기 변환을 제외한 회전과 이동변환으로만 구성된다.
┌ 1 0 0 t_x ┐
T = │ 0 1 0 t_y │
│ 0 0 1 t_z │
└ 0 0 0 1 ┘
┌ X_x Y_x Z_x 0 ┐
R = │ X_y Y_y Z_y 0 │
│ X_z Y_z Z_z 0 │
└ 0 0 0 1 ┘뷰 변환 행렬
- 뷰 행렬을 구하기 위해서는 역행렬을 계산해야한다.
- 이동 T의 역행렬 T^-1은 덧셈의 역원인 반대수를 사용해 구할 수 있다.
- 이동의 역행렬을 적용하면 모든 좌표는 카메라를 중심으로 재배치된다.
- 회전 변환은 전치 행렬로 역행렬인 R^-1을 구할 수 있다.
- 전치하는 이유는 물체가 가만히 있는데 카메라가 30도 회전하는 경우 사용자는 물체가 -30도 회전하는 것으로 느낄 것이기 때문
┌ 1 0 0 -t_x ┐
T^-1 = │ 0 1 0 -t_y │
│ 0 0 1 -t_z │
└ 0 0 0 1 ┘
┌ X_x X_y X_z 0 ┐
R^-1 = │ Y_x Y_y Y_z 0 │
│ Z_x Z_y Z_z 0 │
└ 0 0 0 1 ┘- 최종 뷰 행렬을 구하는 방법
- 뷰 행렬을 구하려면 이동의 역행렬을 먼저 적용할지, 회전의 역행렬을 먼저 적용할지 선택해야 함
- 적용 순서는 이동의 역행렬을 먼저 적용해야한다.
- 이유는 카메라에 회전을 적용할 시점에 모든 좌표는 카메라를 중심으로 변환되어 있어야하기 때문
- 이는 트랜스폼의 순서를 거꾸로 돌리는 것과 동일한 원리
크기 변환 S를 제외한 카메라의 트랜스폼으로부터 얻어지는 모델링 행렬 M
M = T · R
모델링 행렬의 역행렬 M^-1은 뷰 행렬이 된다.
M^-1 = (T · R)^-1 = R^-1 · T^-1
//최종 뷰 행렬 V
┌ -X_x -X_y -X_z x·t ┐
V = R^-1 · T^-1 = │ Y_x Y_y Y_z -y·t │
│ -Z_x -Z_y -Z_z z·t │
└ 0 0 0 1 ┘- 최종 뷰 좌표계는 y축으로 180도 회전한 구조를 가져야한다.
- 따라서 R^-1 · T^-1의 결과 행렬의 x축 기저와 z축 기저를 반전시켜야한다.
오일러 각의 특징
- 오일러 각은 3차원 공간의 회전을 지정할 때 직관적인 인터페이스를 제공한다.
- 표준기저벡터를 회전축으로 사용하기 때문에 회전을 설계하기가 용이하다.
- 적은 용량으로 3차원 공간의 회전 정보를 기록할 수 있다.
짐벌락 현상
- 오일러 각을 사용하면 특정 상황에서 회전의 움직임이 제한되는 짐벌락(Gimbal lock) 현상을 감안해야한다.
- z축을 90도 회전
- x축을 -90도 회전
- y축을 회전하면 처음의 z축 회전과 동일함을 알 수 있다.
회전 보간의 계산
- 경과된 시간에 따라 회전이 변화되도록 중간 회전값을 계산하는 것을 회전 보간(Rotaional interpolation)이라고 한다.
- 중간 회전 값은 선형 보간의 식을 사용해 얻을 수 있다.
θ` = (1-t)θ_start + tθ_end- 예를 들어 동일한 평면 상에서 15°에서 시작해 165°로 끝나는 회전의 1/3비율에 해당하는 회전 보간은 65° 이다.
2/3·15° + 1/3·165° = 65°- 선형 보간식이 성립하려면 두 각의 회전 변환을 곱한 결과가 두 각의 합의 회전 변환과 동일해야한다.
- 2차원 공간의 회전에서는 두 결과가 동일하기 때문에 2차원 공간의 회전에서 선형 보간식을 사용하는데 아무런 문제가 없다.
- 3차원 공간의 오일러 각 회전에서 선형 보간식을 사용할 수 있는지 확인하면 다음과 같다.
세 기저벡터 중 y축에 대해서만 회전하는 오일러 각 회전
y축으로 α와β만큼 회전하는 오일러 각의 데이터는 다음과 같다.
(0, α, 0) (0, β, 0)
두 오일러 각에 대응하는 회전변환 R_α와 R_β는 다음과 같다.
R_α = R_yawα·I·I = R_yawα
R_β = R_yawβ·I·I = R_yawβ
두 오일러 각을 합한 회전 변환 R_(α+β)는 다음과 같다.
R_(α+β) = R_yaw(α+β)·I·I = R_yaw(α+β)
두 오일러 각에 대응하는 회전변환 R_α와 R_β 곱한 결과
R_α·R_β = (R_yawβ·R_pitchβ·R_rallβ)·(R_yawα·R_pitchα·R_rallα)
= (R_yawβ·I·I)·(R_yawα·I·I)
= R_yawβ·R_yawα
= R_(β+α)
= R_yaw(α+β)- y축만 사용하는 두 오일러 각을 곱한 결과는 두 오일러 각을 합한 회전 변환 R_(α+β)와 동일하다.
- 오일러 각에서 한 축만 사용하는 것은 2차원 평면에서의 회전과 동일함
- 한축에 대해서 회전하는 것은 문제가 없지만 두 축에 대해서 회전하는 오일러 각은 선형 보간식을 사용할 수 없다.
x축과 y축 두 축에 대해서 회전하는 오일러 각 회전
두 축에대해 α와β만큼 회전하는 오일러 각의 데이터는 다음과 같다.
(α, α, 0) (β, β, 0)
두 오일러 각에 대응하는 회전변환 R_α와 R_β는 다음과 같다.
R_α = R_yawα·R_pitchα·I = R_yawα·R_pitchα
R_β = R_yawβ·R_pitchβ·I = R_yawβ·R_pitchβ
두 오일러 각을 합한 회전 변환 R_(α+β)는 다음과 같다.
R_(α+β) = R_yaw(α+β)·R_pitch(α+β)·I = R_yaw(α+β)·R_pitch(α+β)
두 오일러 각에 대응하는 회전변환 R_α와 R_β 곱한 결과
R_α·R_β = (R_yawβ·R_pitchαβ·R_rallβ)·(R_yawα·R_pitchβα·R_rallα)
= (R_yawβ·R_pitchβ·I)·(R_yawα·R_pitchα·I)
= R_yawβ·R_pitchβ·R_yawα·R_pitchα
!= R_yaw(α+β)- 일반적으로 게임에서 케릭터 회전은 y축에 대응되는 yaw 회전만을 사용하기 때문에 케릭터 회전 보간은 오일러 각으로 충분히 구현 가능하다.
- 하지만 비행기 조종과 같은 3차원 공간에서 2개 이상의 기저축이 결합된 방식으로 회전을 진행하는 경우 오일러 각 방식을 사용해 회전 보간을 구현하는 것은 어려워진다.
- 3차원 공간에서 자유로운 회전 보간을 구현하고 싶은 경우 로드리게스 회전 공식을 사용하거나 사원수를 사용해야한다.
출처
https://m.yes24.com/Goods/Detail/107025224
이득우의 게임 수학 - 예스24
39가지 실시간 렌더링 게임 프로그래밍 실습 예제를 하나씩 따라 해보며 독자가 직접 체득하는 흥미로운 게임 수학의 세계! 게임 개발자와 그래픽 아티스트들이 궁금해 했던 3D 가상 세계와 메타
m.yes24.com
https://wecandev.tistory.com/214
[이득우 게임수학] 10. 3차원 공간 : 입체 공간의 생성
10.1 3차원 공간의 설계 3차원 공간을 설계하는 방법은 왼손 좌표계와 오른손 좌표계 크게 두가지로 구분된다. 왼손 좌표계는 내가 바라보는 정면이 +z축 이고 위가 +y, 오른쪽이 +x인 방향이다. 오
wecandev.tistory.com
[게임 수학] 3차원 공간 맛보기
🧐 해당 파트는 게임 개발 환경을 구성하는 컴퓨터 그래픽스(Computer Graphics)를 이해하기 위한 기초 수학의 간단한 개념에 대해 설명하고 있습니다!혹여나 이해가 잘 안되거나 잘못된 정보를 발
velog.io
'게임수학' 카테고리의 다른 글
| [게임수학] 원근 투영과 깊이 (1) | 2024.04.23 |
|---|---|
| [게임수학] 벡터의 외적 (0) | 2024.04.23 |
| [게임수학] 정점과 삼각형 (0) | 2024.04.23 |
| [게임수학] 벡터의 내적 (0) | 2024.04.22 |
| [게임수학] 어파인 공간(Affine space) (0) | 2024.04.22 |
