벡터의 외적
- 3차원 벡터의 외적은 x기호를 사용한다.
- 외적의 결과는 내적과 다르게 또다른 벡터이다.
- 이는 연산 결과가 항상 스칼라로 나오는 내적과 대비된다.
- 외적은 행렬식으로도 구할 수 있다.

- 3차원 벡터 u와 v의 외적 u x v는 다음과 같다.
u = (u_x, u_y, u_z), v = (v_x, v_y, v_z)
u x v = (u_y v_z - v_y u_z, u_z v_x - v_z u_x, u_x v_y - v_x u_y)- 외적은 회전의 순환 순서 x -> y -> z -> x에 맞춰 벡터를 순서대로 나열하는 형태이다.
- 와적 계산식의 패턴은 x성분의 결과를 만들기 위해 x와 상관 없는 나머지 두 성분 y와 z를 결합해 만든다는 것이다.
- 나머지 y와 z를 만들 때도 동일함
- 이것도 항상 같은 성분만 사용하는 내적과 대비
- 외적은 교환법칙이 성립하지 않는다.
- 외적은 결합법칙도 성립하지 않는다.
- 단, 덧셈에 대한 분배법칙은 성립한다.
평행성 판별
- 동일한 벡터를 내적하면 벡터 크기를 제곱한 값이 나온다.
- 그러나 동일한 벡터를 외적하면 영벡터가 나온다.
- 또한 평행한 벡터를 외적해도 영벡터가 나온다.
u x u = (u_yu_z - u_yu_z, u_zu_x - u_zu_x, u_xu_y - u_xu_y) = (0, 0, 0)- u와 반대 방향의 벡터 -u를 외적하는 경우에도 동일하다.
u x -u = (-u_yu_z + u_yu_z, -u_zu_x + u_zu_x, -u_xu_y + u_xu_y) = (0, 0, 0)- u와 평행하지만 크기가 다른 v라는 벡터를 외적하여도 결과가 영벡터가 된다.
- 즉, 평행한 두 벡터를 외적하면 항상 영벡터가 나온다는 것을 알 수 있다.
- 외적의 성질은 평행성을 판별하는 데 사용된다.
- 내적의 경우 두 벡터의 직교성을 판별하는 데 사용된다.

- 위 그림처럼 벡터 u를 벡터 v에 수평인 벡터 u_β와 u_⊥로 분리하면 벡터 u는 수평 성분과 수직 성분의 덧셈으로 분리된다.
- 외적은 덧셈의 분배법칙이 성립하므로 벡처 u를 분리한 벡터 u_⊥, u_β와 v의 외적은 다음과 같이 전개된다.
v x u = v x (u_⊥+u_β) = v x u_⊥ + v x u_β
벡터 v와 평행한 벡터 u_β와의 외적은 크기와 관계 없이 영벡터가 된다.
따라서 위 식은 다음과 같이 간략하게 정리된다.
v x u = v x u_⊥- 외적은 상대방에 직교하는 벡터 성분만 사용되는 성질이 있음을 알 수 있다.

- 두 벡터의 사잇각을 Θ라고 할 때 위 그림을 살펴보면 두 벡터의 사잇각이 큰 (a)의 직교하는 성분 u_⊥의 크기는 그보다 사잇각이 작은 (b)의 직교하는 성분 u_⊥보다 크다.
- 직교 성분 u_⊥는 sin 함수에 비례하므로 외적의 크기도 sin 함수에 비례한다.
외적의 결과가 sin 함수에 비례하는지 확인
|u x v|^2 = (u x v)·(u x v)
= (u_x v_z - u_z vz)^2 + (u_z v_x - u_x v_z)^2 + (u_x v_z - u_y v_x)^2
= u_y^2 v_z^2 - 2u_y u_z v_y v_z + u_z^2 v_y^2 + u_z^2 v_x^2
- 2u_y u_y v_z + u_x^2 v_z^2 + u_x^2 v_y^2 - 2u_x u_x v_y + u_y^2 v_x^2
(|u||v|)^2 = (sqrt(u_x^2 + u_y^2 + u_z^2) sqrt(v_x^2 + v_y^2 + v_z^2))^2
= (u_x^2 + u_y^2 + u_z^2)(v_x^2 + v_y^2 + v_z^2)
= u_x^2 v_x^2 + u_x^2 v_y^2 + u_x^2 v_z^2
+ u_y^2 v_x^2 + u_y^2 v_y^2 + u_y^2 v_z^2
+ u_z^2 v_x^2 + u_z^2 v_y^2 + u_z^2 v_z^2
(u·v)^2 = (u_x v_x + u_y v_y + u_z v_z)^2
= (u_x^2 v_x^2 + u_y^2 v_y^2 + u_z^2 v_z^2 + 2u_x u_y v_x v_y
+ 2u_x u_z v_x v_z + 2u_y u_z v_y v_z
세 식의 결과를 비교하면 다음과 같은 관계를 가지는 것을 알 수 있다.
|u x v|^2 = (|u||v|)^2 - (u·v)^2
위 식의 내적 u·v를 코사인 공식으로 바꿔 전개
|u x v|^2 = (|u||v|)^2 - (|u||v|cosΘ)^2
= (|u||v|)^2(1 - cos^2Θ)
= (|u||v|)^2 sin^2Θ- 따라서 벡터 외적의 크기는 sin 함수에 비례한다는 것을 알 수 있다.
|u x v| = |u| |v| |sinθ|
- 외적으로 생성된 벡터의 크기는 위 그림과 같이 두 벡터가 만드는 평행사변형의 넓이로 나타낼 수 있다.
외적의 특성
- A와 B의 벡터의 외적, AxB는 A와도 수직이고, B와도 수직이다.
- 내적과 달리 교환 법칙이 성립하지 않으며 순서를 바꾸면 반대 방향의 벡터가 나온다.
- AxB = -(BxA)
- 내적과 동일하게 분배 법칙은 성립한다.
- Ax(B+C) = (AxB) + (AxC)
- 외적 벡터의 크기는 평행사면형의 넓이이다.
- 두 벡터가 평행하면 크기는 0이다.
- sin값이 0이기 때문이다.
법선 벡터
- 벡터 외적은 두 벡터에 직교하는 벡터를 생성한다.
- 두 벡터 u, v 가 있을때 u와 v의 외적결과에 u를 내적하면 0이 된다.
- 반대로 u와 v의 외적결과에 v를 내적해도 0이 된다.
- 그래서 외적의 결과는 두 벡터에 모두 직교함을 알수 있다.
u·(u x v) = u_x u_y v_z - u_x v_y u_z + u_y u_z v_x
- u_y v_z u_x + u_z u_x v_y - u_z v_x u_y = 0
- 점 P1, P2, P3 를 결합해 만든 평면이 있다고 할 때
- u = P2 - P1, v = P3 - P1 이 둘을 외적하면 세 점이 만들어내는 평면에 직교하는 벡터가 생성될 것
- 이는 평면이 향하는 방향을 나타내며 이 벡터를 법선 벡터(Normal vector)라고 한다.

- 외적은 교환법칙이 성립하지 않기 때문에 u x v와 v x u는 서로 반대 방향으로 법선 벡터가 생성된다.
- 3차원 공간에서 평면은 앞면과 뒷면으로 구성되어 있기 떄문에 두 개의 다른 벡터가 나오게 된다.
- 오른손 좌표계를 사용하는 경우 외적의 결과는 오른손 법칙을 따른다.
- 평면의 앞면을 파악하고 싶을때 아래 그림과 같이 엄지손가락이 향하는 방향을 파악하면 된다.

좌우 방향 판별
- sin 함수와 관련 있는 외적의 성질은 게임 개발에서 유용하게 활용할 수 있다.
- 대표적인 외적의 활용 방법은 왼쪽과 오른쪽의 판별이다.

- 캐릭터 정면 시선 벡터를 F, 캐릭터에서 대상으로 향하는 벡터가 A, y축 (0,1,0) 벡터를 UP 이라고 할 때
- A와 F를 외적하고 UP을 내적한 결과를 가지고 좌우 방향을 판별 할 수 있다.
- 만약 물체가 시선 뱡향의 왼쪽에 있다면 시선벡터에서 물체로 향하는 벡터로 외적한 결과는 오른손 법칙에 따라 평면의 위쪽으로 향하게 될 것이다.
- 반대로 물체가 시선 방향의 오른쪽에 있다면 외적의 결과는 평면의 아래쪽 방향으로 향할 것이다.
- 외적의 성질을 활용하면 시선 방향을 기준으로 물체가 왼쪽에 있는지 오른쪽에 있는지를 파악할 수 있다.
- 외적의 결과는 벡터이므로, 참 거짓을 파악할 수 있도록 스칼라로 변환해야 함
- 이를 위해 외적의 결과에 내적을 추가로 활용해야 한다.
- 외적 결과에 평면의 위쪽 방향을 나타내는 벡터를 내적하면
- 두 벡터의 방향이 같다면 내적 결과는 양수, 반대 방향이라면 음수가 된다.
- 따라서 물체가 케릭터의 시선 방향 왼쪽에 있다면 내적의 결과는 양수, 오른쪽에 있다면 음수가 될 것이다.
- 외적과 내적 연산을 조합해 파악할 수 있는 경우의 수는 다음과 같다.
- (A x F) · UP > 0 : 물체가 시선 방향에서 왼쪽에 있음
- (A x F) · UP < 0 : 물체가 시선 방향에서 오른쪽에 있음
- (A x F) · UP == 0 : 물체가 시선 방향에 있음
- 이러한 좌우 방향 판별에 사용되는 외적의 응용은 sin 함수에 비레하는 외적의 성질에 기인한다고 할 수 있다.
- 반면 내적은 cos 함수에 비례하기 때문에 앞 뒤 방향 판별에 사용된다.
벡터로부터 회전행렬 생성
- 직교하는 벡터를 생성하는 외적의 성질은 카메라의 회전을 설정하는데도 사용된다.

- 위 그림과 같이 3차원 공간에서 좌우로 기울어지지 않은 카메라가 아래쪽에 위치한 물체를 바라보고 있는 상황이 있는 경우
- 오일러 각 방식을 사용해 카메라의 회전을 지정할 수 있자만, 외적을 사용하면 카메라의 시선 벡터 정보로부터 카메라의 세 가지 로컬 축을 구하고 이러부터 회전행렬까지 얻어낼 수 있다.
- 세 로컬 축을 구하는 방법을 단계별로 알아보자

- 먼저 위 그림처럼 물체의 위치에서 카메라의 위치를 뺀 후 크기를 1로 정규화시킨 시선벡터 v를 생성하면, 이 벡터는 카메라 트랜스폼의 로컬 z축이 될 것이다.
- 카메라의 로컬 x축은 위 그림에서 보이는 것 처럼 업벡터(Up vector)라고 불리는 월드 공간의 y축과 카메라의 로컬 z축을 외적하면 얻을 수 있다.
- 마지막으로 로컬 z축과 로컬 x축을 외적하면 남은 로컬 y축을 구할 수 있다.
- 이때는 두 벡터가 단위 벡터이므로 외적의 결과도 단위 벡터가 될 것이다.
- 정리하면 카메라가 바라보는 시선 벡터 v가 주어지는 업벡터로부터 로컬 공간을 구성하는 세기저벡터 x, y, z를 다음과 같이 구할 수 있다.
x = u x z / |u x z|
y = z x x
z = v/|v|- 카메라 트랜스폼의 회전행렬 R은 로컬 벡터를 열벡터로 지정해 다음과 같이 생성할 수 있다.
┌ X_x Y_x Z_x 0 ┐
R = │ X_y Y_y Z_y 0 │
│ X_z Y_z Z_z 0 │
└ 0 0 0 1 ┘- 시선 벡터로부터 카메라 로컬 축을 계산하는 데 있어 추가로 고려해야 할 예외 상황이 있다.
- 그중 하나는 카메라의 위쪽 방향이다.
- 앞서 살펴본 상황은 카메라의 위쪽 방향이 월드 공간의 y축을 향한다고 가정한 것이다.
- 하지만 아래 그림과 같이 카메라가 뒤집혀 있는 상황인 경우, 로컬 x축을 구하기 위한 업벡터로 월드 공간 y축의 반대 방향인 (0, -1, 0)을 사용해야 한다.

- 일반적인 상황에서는 카메라가 위를 향해 세워져 있겠지만, 그렇지 않은 경우도 간혹 발생할 수 있으니 외적에 사용될 업벡터의 값을 입력받도록 설계하는 것이 안전하다.

- 그다음 고려할 예외 상황으로는 위 그림과 같이 로컬 z축이 업벡터와 평행할 때다.
- 두 벡터가 평행하면 외적 결과가 영벡터가 되어 더 이상 계산을 진행할 수 없다.
- 이 경우 외적을 계산하는 대신, 로컬 z축에 직교하는 로컬 x축의 값을 수동으로 지정해야 한다.
백페이스 컬링
- 게임은 실시간으로 빠르게 렌더링을 처리해야 하기 때문에 카메라에 노출되지 않는 메시(Mesh)의 뒷면(Backface)은 그리지 않는 것이 효과적이다.
- 이런 뒷면을 생략하는 기법을 백페이스 컬링(Backface culling)이라고 한다.
- 백페이스 컬링은 메시의 삼각형을 구성하는 세 정점의 외적을 활용해 구현할 수 있다.
- 아래 그림과 같이 삼각형을 구성하는 메시 데이터가 설정된 상황을 생각해보자

- 삼각형의 세 점을 지정하는 인덱스 버퍼에는 점의 순서가 나열되어 있다.
- 이를 활용하여 삼각형의 방향을 지정하지 않아도 외적을 사용해 삼각형이 향하는 방향을 파악할 수 있다.

- 위 그림통해 인덱스 버퍼의 순서에 따라 삼각형의 방향이 어떻게 결정되는지를 알 수 있다.
- (a)는 시계 방향으로 정점이 나열되어 있으므로 삼각형이 향하는 방향은 지면의 뒤편을 향하게 된다.
- (b)는 반시계 방향으로 정점이 나열되어 있어서 지면을 향할 것이다.
- 이렇게 정한 삼각형의 방향과 카메라의 시선 방향을 대조해 서로 마주보면 삼각형을 그리고, 같은 방향을 바라보면 그리기를 생략하는 것이 백페이스 컬링의 알고리즘이다.

- 이에 대한 원리는 위 그림을 통해 알 수 있다.
- (a)는 삼각형의 방향과 카메라의 시선 방향이 같은 방향을 향하고 있다. 따라서 해당 삼각형은 그리기를 생략해 렌더링 계산량을 줄일 수 있다.
- (b)는 삼각형의 방향과 카메라의 시선 방향이 마주보고 있다. 따라서 해당 삼각형은 그려준다.
로드리게스 회전 공식
- 3차원 회전을 관리하기 위해 오일러 각을 사용하고 있지만, 오일러 각은 짐벌락 현상이 발생하고, 회전 보간이 어렵다는 문제가 있었다.
- 오일러 각의 문제는 임의의 축에 대한 평면의 회전 방식을 사용하여 해결 가능하다.
- 이 방식을 축-각 회전(Axis-Angle rotation)이라 부른다.

- 축-각 회전은 위 그림과 같이 3차원 공간에서 지정된 임의의 축에 직교하는 평면에서 회전이 진행되는 형태를 띈다.

- 축-각 회전을 수행하는 회전 공식은 내적과 외적을 사용해 직접 유도해볼 수 있다.
- 위 그림과 같이 관련된 점과 벡터에 각각 기호를 붙였다.
- 회전축은 회전이 발생하는 평면에 직교하는 법선 벡터다.
- 이를 벡터 n으로 지정하고 편의를 위해 크기를 1로 정규화시킨다.
- 회전시킬 점을 P, 점가 각 Θ만큼 회전한 최종 점을 P'으로 표기하고, 월드 공간의 원점을 O로, 회전 평면의 중심점을 O'으로 지정한다.
- 이때 점 P의 좌표는 (x, y, z, 1)로 설정한다.
- 원점 O에서부터 회전시킬 점 P까지의 벡터를 u로 지정하고, 점 P와 벡터 u의 값은 마지막 차원의 값만 다를 뿐 (x, y, z)는 동일하다. 따라서 구할 점 P'의 좌표는 벡터 u를 구하면 얻을 수 있다.
u = P - O = (x, y, z, 0)- 임의의 축 n에 대해 벡터 u를 각 Θ만큼 회전시켜 벡터 u'을 계산하는 축-각 회전 공식은 다음과 같다.
u' = cosΘ·u + (1-cosΘ)·(u·n)·n + sinΘ·(n x u)
- 원점에서 회전시킬 점으로 향하는 벡터 u를 평면의 회전축에 해당하는 법선 벡터 n에 투영하면, 투영할 벡터의 크기가 2이므로 투영 공식에 의해 벡터 OO'의 값은 (u·n)·n이 된다.
- 이를 줄여서 벡터 v로 칭한다.
- 위 그림에서 보여지는 공간의 원점에서 회전 평면의 원점으로 향하는 벡터 v는 다음과 같이 계산된다.
OO' = v = (u·n)·n- 회전 평면의 중점 O'에서 점P으로 향하는 벡터 O'P는 두 벡터의 차가 되므로 u - v가 될 것이다.

- 회전 평면을 위에서 내려다보면 회전이 어떻게 동작하는지 관찰할 수 있다.
- 위 그림은 위에서 회전 평면을 내려다본 것이다.
- 이 평면의 벡터 O'P를 각 Θ만큼 회전시킨 벡터 O'P'을 구하는 것이 목표가 될 것이다.

- 벡터 O'P'를 가로 성분과 세로 성분으로 분리하면, 가로 성분에 해당하는 벡터는 위 그림과 같이 벡터 O'P에 cosΘ를 곱해 얻을 수 있다.

- 나머지 세로 성분에 해당하는 벡터를 구하기 위해선 같은 방향을 향하는 벡터가 필요한데 이는 위 그림과 같이 법선 벡터 n과 벡터 O'P를 외적해 얻을 수 있다.
- 이를 벡터 O'Q로 지정하면 벡터 O'Q는 다음과 같이 구할 수 있다.
O'Q = n x (u - v)- 벡터 O'Q에 sinΘ를 곱하면 세로 성분에 해당하는 벡터를 얻을 수 있다.
- 두 벡터를 모두 얻었으니 다음 수식으로 벡터 O'P를 각 Θ만큼 회전한 벡터 O'P'의 값을 얻게 된다.
O'P' = cosΘ · O'P + sinΘ · O'Q
위 식을 벡터 n, u와 v를 사용해 전개
O'P' = cosΘ · (u - v) + sinΘ · (n x (u - v))
분배 법칙을 적용해 전개
O'P' = cosΘ · (u - v) + sinΘ · (n x u - n x v)
벡터 n와 v는 평행하므로 우변 끝에 위치한 외적 n x v의 값은 영벡터가 된다.
O'P' = cosΘ · (u - v) + sinΘ · (n x u)
- 마지막으로 구해야할 최종 벡터 OP'은 위 그림과 같이 선분 O'P'에 벡터 v를 더해 얻을 수 있다.
OP' = v + cosΘ · (u - v) + sinΘ · (n x u)
벡터 v를 (u·n)·n으로 치환하면 최종 수식이 유도된다.
u' = cosΘ·u + (1-cosΘ)·(u·n)·n + sinΘ·(n x u)- 위 공식은 1840년에 프랑수 수학자 로드리게스가 발표했으며, 이름을 인용해 로드리게스 회전 공식이라고 한다.
삼중곱
- 벡터의 외적과 내적을 두 번 연속 사용하는 삼중곱(Triple product)연산은, 세 개의 벡터 u,v,w 를 사용하여 내적과 외적의 순서에 따라 4가지 경우의 수가 발생한다.
1. u · (v · w)
2. u · (v x w)
3. u x (v · w)
4. u x (v x w)- 그러나 1번은 괄호 안의 벡터 내적의 결과값은 스칼라가 되므로 벡터를 세번 곱햇다고 보기 어렵다.
- 3번의 경우 벡터와 스칼라는 외적할 수 없으므로 연산이 불가능 하다.
- 2,4번만이 유효한 삼중곱 연산이다.
스칼라 삼중곱
- 2번 연산은 (u · (v x w)) 스칼라 삼중곱(Scalar triple product)이라고 부른다.
- 왼쪽과 오른쪽의 판별 방법과 백페이스 컬링에 사용한 공식이 모두 스칼라 삼중곱이다.

- 스칼라 삼중곱 연산의 의미를 시작적으로 파악하기 위해 외적으로 만든 벡터의 크기는 두 벡터가 이루는 평행사변형의 크기임과 동시에 외적으로 만들어진 법선 벡터의 크기임 표현한 그림을 그리면 위와 같다.

- 이 상황에서 임의의 벡터 u의 크기를 법선 벡터 v x w에 수직으로 투영한 벡터의 높이는 위 그림처럼 cos 함수에 비례한다.

- 높이 |u|cosΘ에 평행사변형의 넓이 |v x w|를 곱하면 위 그림에서 볼 수 있는 육면체의 부피가 나올 것이다.
- 이는 스칼라 삼중곱이 만들어내는 값의 절대값과 동일하다.
- 즉, 스칼라 삼중곱의 절대값은 세 벡터 u, v, w가 만드는 평행육면체의 부피를 의미한다.
- 세 벡터에서 바닥에 해당하는 두 벡터를 다른 벡터로 변경해도 최종 육면체의 부피 값은 변하지 않으므로 삼중곱의 결과는 동일하다.
- 부호에 유의해 벡터 u, v, w가 만들어내는 스칼라 삼중곱은 다음과 같은 성질을 가진다.
u · (v x w) = v · (w x u) = w · (u x v)- 스칼라 삼중곱은 3차원 공간의 세 벡터가 모두 선형 독립의 관계를 가지는지 판단하는 판별식으로 생각할 수 있다.
- 결과값이 0이 아니면 세 벡터는 모두 선형 독립의 관계를 가진다.
벡터 삼중곱
- 4번 연산은 (u x (v x w)) 벡터 삼중곱(Vector triple product)이라고 한다.
u x (v x w) = (u · w) · v - (u · v) · w- 위의 식을 삼중곱 전개(Triple product expansion)또는 라그랑주 공식(Lagrange's formula)이라 한다.
- 좌변 식의 최종 연산은 외적이므로 이의 결과는 벡터로 나옴을 알 수 있다.
- 최종 벡터의 x성분만 먼저 전개한다면, 먼저 v x w의 외적을 계산하는 식은 다음과 같다.
v x w = (v_y w_z - w_y v_z, v_z w_x - w_z v_x, v_x w_y - w_x v_y)- 이때 외적의 x요소에는 u벡터와 (v x w)벡터의 y 성분과 z 성분만 사용된다.
- u x (v x w)로 만들어지는 x 성분을 전개하면 아래와 같다.
u x (v x w)_x = u_y(v_x w_y - w_x v_y) - (v_z w_x - w_z v_x)u_z
= v_x(u_y w_y + u_z w_z) - w_x(u_y u_y + u_z v_z)
= v_z(u_y w_y + u_z w_z) - w_x(u_y u_y + u_z v_z)
+ v_x u_x w_x - v_x u_x w_x
= v_x(u_x w_x + u_y w_y + u_z w_z) - w_x(u_x v_x + u_y v_y + u_z v_z)
= v_x(u · w) - w_x(u · v)- 나머지 두 개의 성분도 동일한 방식으로 전개할 수 있으며, 이 결과를 정리하면 다음과 같다.
u x (v x w)_y = v_y(u · w) - w_y(u · v)
u x (v x w)_z = v_z(u · w) - w_z(u · v)- 다소 복잡한 외적을 두개의 내적 연산으로 변환한다는 특징을 지닌다.
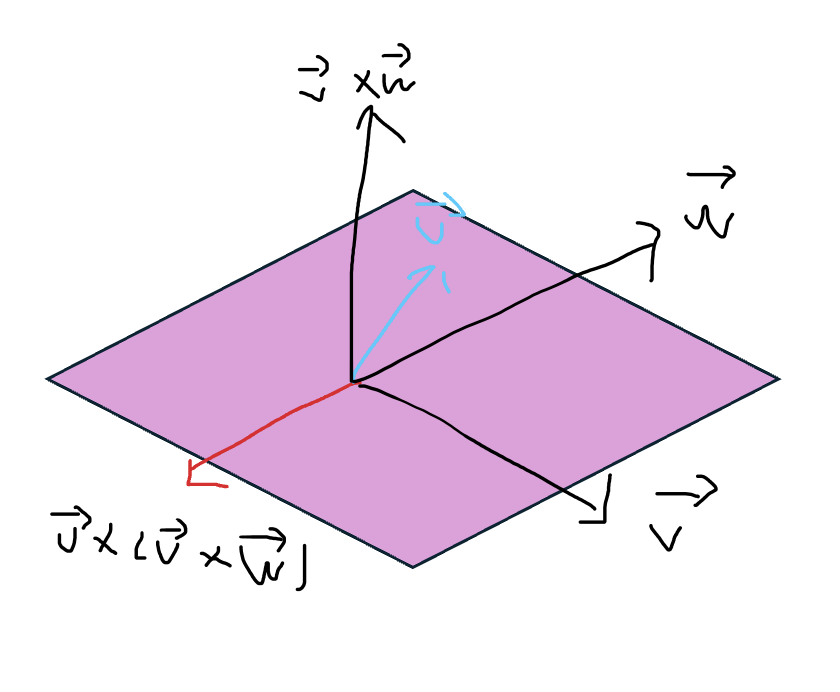
- 벡터 삼중곱으로 만들어지는 벡터는 두 벡터가 만드는 평면에 속함을 알 수 있다.
출처
https://m.yes24.com/Goods/Detail/107025224
이득우의 게임 수학 - 예스24
39가지 실시간 렌더링 게임 프로그래밍 실습 예제를 하나씩 따라 해보며 독자가 직접 체득하는 흥미로운 게임 수학의 세계! 게임 개발자와 그래픽 아티스트들이 궁금해 했던 3D 가상 세계와 메타
m.yes24.com
https://wecandev.tistory.com/216
[이득우 게임수학] 11. 외적: 3차원 공간의 분석과 응용
11.1 벡터의 외적 3차원 벡터의 외적은 x기호를 사용한다. 3차원 벡터 u와 v의 외적 u x v는 다음과 같다 u = (u_x, u_y, u_z), v = (v_x, v_y, v_z) u x v = (u_y v_z - v_y u_z, u_z v_x - v_z u_x, u_x v_y - v_x u_y) 외적은 교환
wecandev.tistory.com
[면접기술] 벡터의 외적과 내적
게임 프로그래밍에서 왜 벡터를 쓰는가?게임상의 오브젝트들의 정보를 나타낼 때, 좀 더 간단하고 편하게 나타내기 위해서 사용.벡터로 속도, 바람, 저항, 충돌, 위치 판단 등 많은 것들을 표현
velog.io
'게임수학' 카테고리의 다른 글
| [게임수학] 절두체(Frustum) (0) | 2024.04.25 |
|---|---|
| [게임수학] 원근 투영과 깊이 (1) | 2024.04.23 |
| [게임수학] 3차원 공간 (0) | 2024.04.23 |
| [게임수학] 정점과 삼각형 (0) | 2024.04.23 |
| [게임수학] 벡터의 내적 (0) | 2024.04.22 |
