Trie(트라이)?
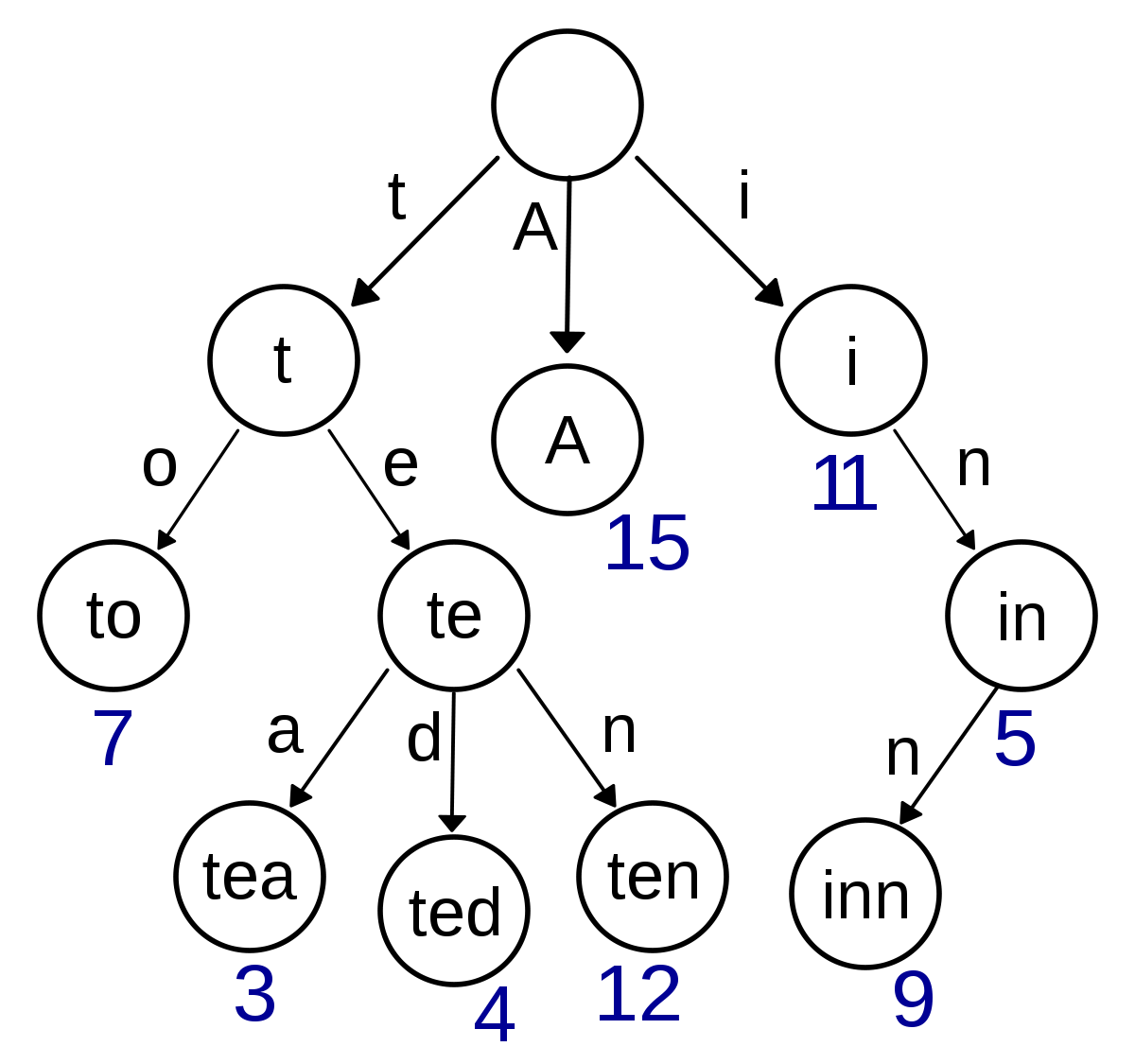
- 트라이는 문자열을 저장하고 효율적으로 탐색하기 위한 트리형태의 자료구조이다.
- 우리가 검색할 때 볼 수 있는 자동완성 기능, 사전 검색 등 문자열을 탐색하는데 특화되어있는 자료구조라고 한다.
- 래딕스 트리(radix tree), 접두사 트리(prefix tree)혹은 탐색 트리(retrieval tree)라고도 한다.
- 트라이는 retrieval tree에서 나온 단어이다.
- 예) Datastructure라는 단어를 검색하기 위해서는 제일 먼저 'D'를 찾고, 다음에 'a', 't', ... 의 순서로 찾으면 된다. 이러한 개념을 적용한 것이 트라이(Trie)이다.
- 정수형에서 이진탐색트리를 이용하면 시간복잡도 O(logN)
- 하지만 문자열에서 적용했을 때, 문자열 최대 길이가 M이면 O(M*logN)이 된다.
- 트라이를 활용하면? → O(M)으로 문자열 검색이 가능함
장단점
- 트라이(Trie)는 문자열 검색을 빠르게 한다.
- 문자열을 탐색할 때, 하나하나씩 전부 비교하면서 탐색을 하는 것보다 시간 복잡도 측면에서 훨씬 더 효율적이다.
- 각 노드에서 자식들에 대한 포인터들을 배열로 모두 저장하고 있다는 점에서 저장 공간의 크기가 크다는 단점도 있다.
- 메모리 측면에서 비효율적일 수 있음
트리이 삽입 과정
- 'abc', 'ab', 'car' 단어들을 'abc'부터 트라이에 저장한다고 가정
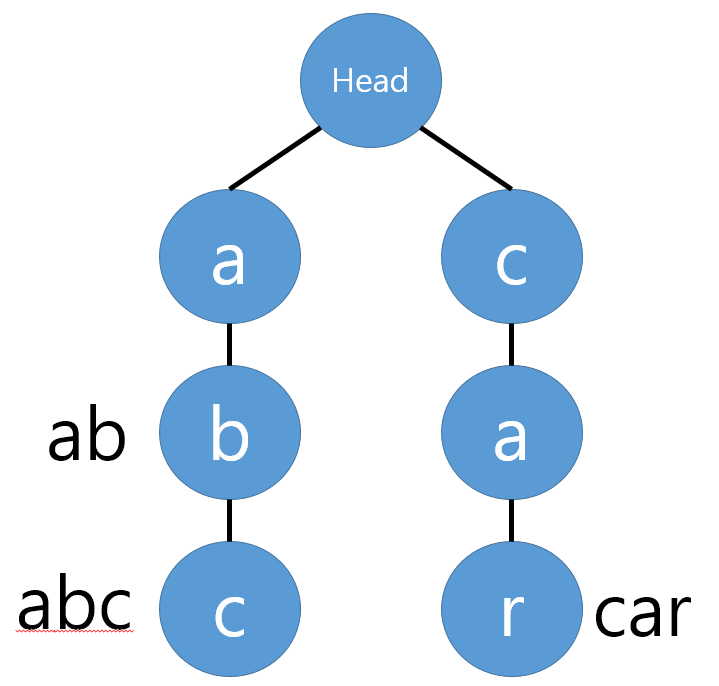
- abc 삽입
- 첫 번째 문자는 'a'이다. 초기에 트라이 자료구조 내에는 아무것도 없으므로 Head의 자식노드에 'a'를 추가해준다.
- 'a'노드에도 현재 자식이 하나도 없으므로, 'a'의 자식노드에 'b'를 추가해준다.
- 'c'도 마찬가지로 'b'의 자식노드로 추가해준다.
- 'abc' 단어가 여기서 끝남을 알리기 위해 현재 노드에 abc라고 표시한다. (Data)
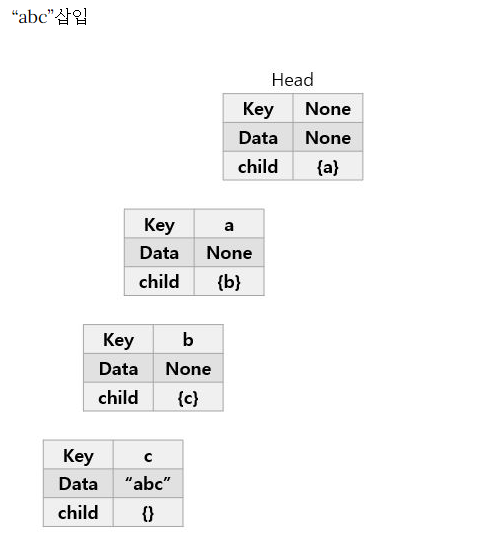
- ab 삽입
- 현재 Head의 자식노드로 'a'가 이미 존재한다. 따라서 'a'노드를 추가하지 않고, 기존에 있는 'a'노드로 이동한다.
- 'b'도 'a'의 자식노드로 이미 존재하므로 'b'노드로 이동한다.
- 'ab' 단어가 여기서 끝이므로 현재 노드에 ab를 표시한다.
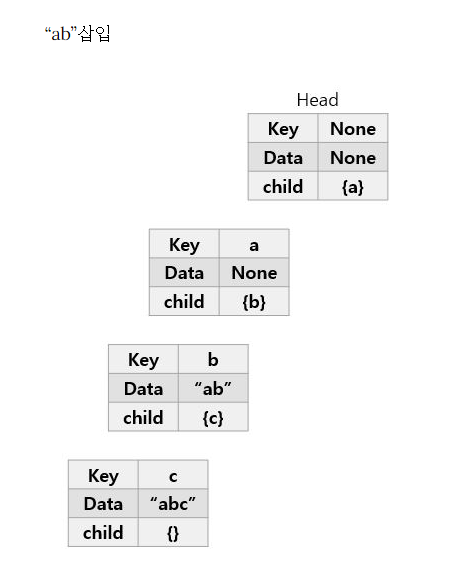
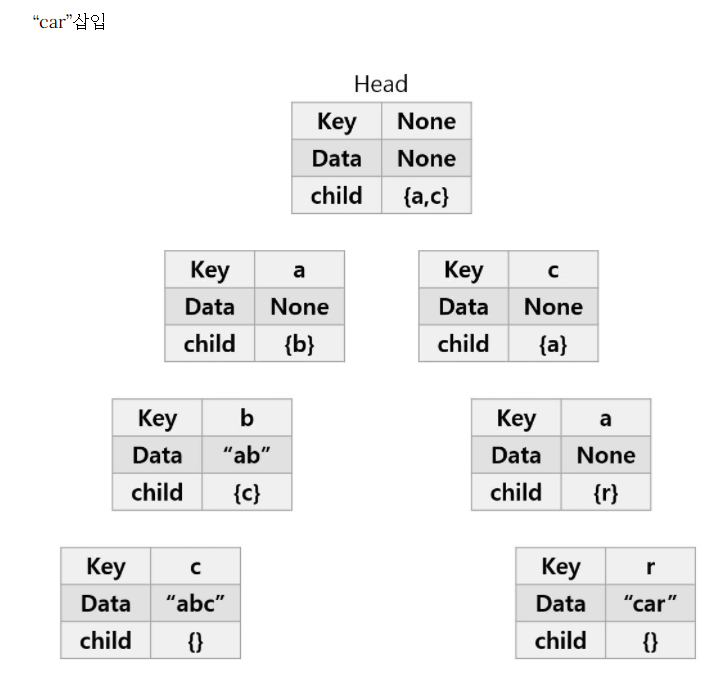
- car 삽입
- Head의 자식노드로 'a'만 존재하고, 'c'는 존재하지 않는다. 따라서 'c'를 자식노드로 추가한다.
- 'c'의 자식노드가 없으므로 마찬가지로 'a'를 추가한다.
- 'a'의 자식노드가 없으므로 마찬가지로 'r'을 추가한다.
- 'car' 단어가 여기서 끝이므로 현재 노드에 car를 표시한다.
트라이 탐색 과정
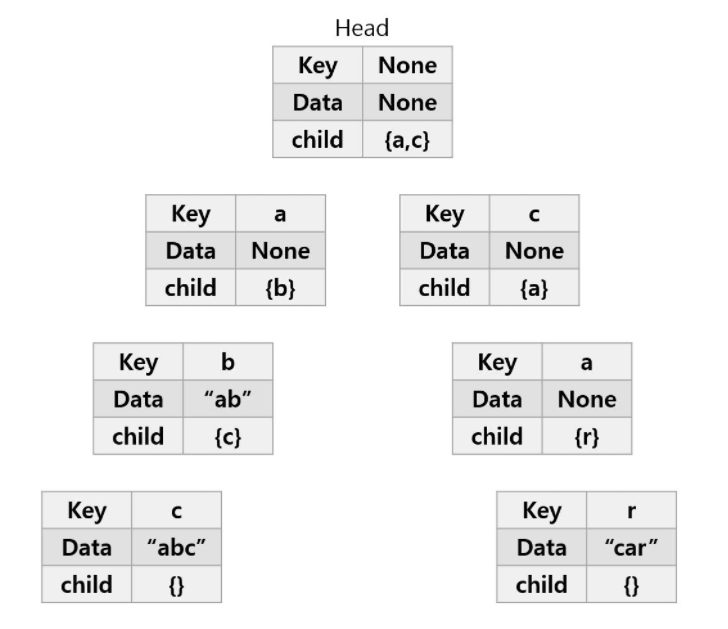
- 위의 트라이에 'abc' 문자열이 있는지 탐색
- Head의 child에 'a'가 존재 --> 'a'노드(key='a')로 이동
- 'a'노드의 child에 'b'가 존재 --> 'b'노드(key='b')로 이동
- 'b'노드의 child에 'c'가 존재 --> 'c'노드(key='c')로 이동
- 문자열 탐색이 완료됨 --> 현재 노드('c'노드)에 Data값이 존재!
- 따라서 'abc'라는 문자열이 존재함을 알 수 있다.
- 'ca'라는 문자열이 있는지 탐색
- Head의 child에 'c'가 존재 --> 'c'노드(key='c')로 이동
- 'c'노드의 child에 'a'가 존재 --> 'a'노드(key='a')로 이동
- 문자열 탐색이 완료됨 --> 현재 노드('a'노드)에 Data값이 없음!
- 따라서 'ca'라는 문자열은 존재 X
트리이 구현
#include<iostream>
#include<string>
using namespace std;
class Trie{
public:
bool isEnd;
Trie* children[26];
Trie() : children(), isEnd(false) {}
void insert(string& key, int index){
if(index == key.length() - 1)
isEnd = true;
else{
int next = key[index] - 'a';
if(children[next] == NULL)
children[next] = new Trie();
children[next]->insert(key,index+1);
}
}
// 접두사로서 검색 되더라도 true를 리턴
bool find1(string& key, int depth){
if(depth == key.length() - 1) return true;
int next = key[depth] - 'a';
if(children[next] == NULL)
return false;
return children[next]->find1(key,depth+1);
}
// 완전히 일치하는 단어 단위로만 찾고 true를 리턴
bool find2(string key, int depth){
if(depth==key.length() - 1&& isEnd)
return true;
if(depth == key.length() - 1&&!isEnd)
return false;
int next = key[depth] - 'a';
if(children[next]==NULL)
return false;
return children[next]->find2(key,depth+1);
}
};
int main() {
string words[] = { "what", "when", "yours", "apple", "her", "his", "you" };
Trie root;
for (int i = 0;i<7;i++)
root.insert(words[i], 0);
string search = "wh";
if (root.find1(search, 0)) cout << search << "가 검색 결과에 있습니다." << '\n';
else cout << search << "가 검색 결과에 없습니다." << '\n';
if (root.find2(search, 0)) cout << search << "가 검색 결과에 있습니다." << '\n';
else cout << search << "가 검색 결과에 없습니다." << '\n';
}
출처
https://velog.io/@kimdukbae/%EC%9E%90%EB%A3%8C%EA%B5%AC%EC%A1%B0-%ED%8A%B8%EB%9D%BC%EC%9D%B4-Trie
[자료구조] 트라이 (Trie)
트라이(Trie)는 문자열을 저장하고 효율적으로 탐색하기 위한 트리 형태의 자료구조이다.우리가 검색할 때 볼 수 있는 자동완성 기능, 사전 검색 등 문자열을 탐색하는데 특화되어있는 자료구조
velog.io
https://ansohxxn.github.io/algorithm/trie/#google_vignette
(C++) 문자열 집합 : 트라이 자료구조
🚀 트라이 자료구조
ansohxxn.github.io
https://github.com/gyoogle/tech-interview-for-developer
GitHub - gyoogle/tech-interview-for-developer: 👶🏻 신입 개발자 전공 지식 & 기술 면접 백과사전 📖
👶🏻 신입 개발자 전공 지식 & 기술 면접 백과사전 📖. Contribute to gyoogle/tech-interview-for-developer development by creating an account on GitHub.
github.com
'CS > Data Structure' 카테고리의 다른 글
| [Data Structure] Hash (0) | 2024.04.03 |
|---|---|
| [Data Structure] B-Tree&B+Tree (0) | 2024.04.03 |
| [Data Structure] Binary Search Tree (1) | 2024.03.31 |
| [Data Structure] Tree (0) | 2024.03.31 |
| [Data Structure] Heap (0) | 2024.03.31 |
Trie(트라이)?

- 트라이는 문자열을 저장하고 효율적으로 탐색하기 위한 트리형태의 자료구조이다.
- 우리가 검색할 때 볼 수 있는 자동완성 기능, 사전 검색 등 문자열을 탐색하는데 특화되어있는 자료구조라고 한다.
- 래딕스 트리(radix tree), 접두사 트리(prefix tree)혹은 탐색 트리(retrieval tree)라고도 한다.
- 트라이는 retrieval tree에서 나온 단어이다.
- 예) Datastructure라는 단어를 검색하기 위해서는 제일 먼저 'D'를 찾고, 다음에 'a', 't', ... 의 순서로 찾으면 된다. 이러한 개념을 적용한 것이 트라이(Trie)이다.
- 정수형에서 이진탐색트리를 이용하면 시간복잡도 O(logN)
- 하지만 문자열에서 적용했을 때, 문자열 최대 길이가 M이면 O(M*logN)이 된다.
- 트라이를 활용하면? → O(M)으로 문자열 검색이 가능함
장단점
- 트라이(Trie)는 문자열 검색을 빠르게 한다.
- 문자열을 탐색할 때, 하나하나씩 전부 비교하면서 탐색을 하는 것보다 시간 복잡도 측면에서 훨씬 더 효율적이다.
- 각 노드에서 자식들에 대한 포인터들을 배열로 모두 저장하고 있다는 점에서 저장 공간의 크기가 크다는 단점도 있다.
- 메모리 측면에서 비효율적일 수 있음
트리이 삽입 과정
- 'abc', 'ab', 'car' 단어들을 'abc'부터 트라이에 저장한다고 가정

- abc 삽입
- 첫 번째 문자는 'a'이다. 초기에 트라이 자료구조 내에는 아무것도 없으므로 Head의 자식노드에 'a'를 추가해준다.
- 'a'노드에도 현재 자식이 하나도 없으므로, 'a'의 자식노드에 'b'를 추가해준다.
- 'c'도 마찬가지로 'b'의 자식노드로 추가해준다.
- 'abc' 단어가 여기서 끝남을 알리기 위해 현재 노드에 abc라고 표시한다. (Data)

- ab 삽입
- 현재 Head의 자식노드로 'a'가 이미 존재한다. 따라서 'a'노드를 추가하지 않고, 기존에 있는 'a'노드로 이동한다.
- 'b'도 'a'의 자식노드로 이미 존재하므로 'b'노드로 이동한다.
- 'ab' 단어가 여기서 끝이므로 현재 노드에 ab를 표시한다.

- car 삽입
- Head의 자식노드로 'a'만 존재하고, 'c'는 존재하지 않는다. 따라서 'c'를 자식노드로 추가한다.
- 'c'의 자식노드가 없으므로 마찬가지로 'a'를 추가한다.
- 'a'의 자식노드가 없으므로 마찬가지로 'r'을 추가한다.
- 'car' 단어가 여기서 끝이므로 현재 노드에 car를 표시한다.

트라이 탐색 과정

- 위의 트라이에 'abc' 문자열이 있는지 탐색
- Head의 child에 'a'가 존재 --> 'a'노드(key='a')로 이동
- 'a'노드의 child에 'b'가 존재 --> 'b'노드(key='b')로 이동
- 'b'노드의 child에 'c'가 존재 --> 'c'노드(key='c')로 이동
- 문자열 탐색이 완료됨 --> 현재 노드('c'노드)에 Data값이 존재!
- 따라서 'abc'라는 문자열이 존재함을 알 수 있다.
- 'ca'라는 문자열이 있는지 탐색
- Head의 child에 'c'가 존재 --> 'c'노드(key='c')로 이동
- 'c'노드의 child에 'a'가 존재 --> 'a'노드(key='a')로 이동
- 문자열 탐색이 완료됨 --> 현재 노드('a'노드)에 Data값이 없음!
- 따라서 'ca'라는 문자열은 존재 X
트리이 구현
#include<iostream>
#include<string>
using namespace std;
class Trie{
public:
bool isEnd;
Trie* children[26];
Trie() : children(), isEnd(false) {}
void insert(string& key, int index){
if(index == key.length() - 1)
isEnd = true;
else{
int next = key[index] - 'a';
if(children[next] == NULL)
children[next] = new Trie();
children[next]->insert(key,index+1);
}
}
// 접두사로서 검색 되더라도 true를 리턴
bool find1(string& key, int depth){
if(depth == key.length() - 1) return true;
int next = key[depth] - 'a';
if(children[next] == NULL)
return false;
return children[next]->find1(key,depth+1);
}
// 완전히 일치하는 단어 단위로만 찾고 true를 리턴
bool find2(string key, int depth){
if(depth==key.length() - 1&& isEnd)
return true;
if(depth == key.length() - 1&&!isEnd)
return false;
int next = key[depth] - 'a';
if(children[next]==NULL)
return false;
return children[next]->find2(key,depth+1);
}
};
int main() {
string words[] = { "what", "when", "yours", "apple", "her", "his", "you" };
Trie root;
for (int i = 0;i<7;i++)
root.insert(words[i], 0);
string search = "wh";
if (root.find1(search, 0)) cout << search << "가 검색 결과에 있습니다." << '\n';
else cout << search << "가 검색 결과에 없습니다." << '\n';
if (root.find2(search, 0)) cout << search << "가 검색 결과에 있습니다." << '\n';
else cout << search << "가 검색 결과에 없습니다." << '\n';
}
출처
https://velog.io/@kimdukbae/%EC%9E%90%EB%A3%8C%EA%B5%AC%EC%A1%B0-%ED%8A%B8%EB%9D%BC%EC%9D%B4-Trie
[자료구조] 트라이 (Trie)
트라이(Trie)는 문자열을 저장하고 효율적으로 탐색하기 위한 트리 형태의 자료구조이다.우리가 검색할 때 볼 수 있는 자동완성 기능, 사전 검색 등 문자열을 탐색하는데 특화되어있는 자료구조
velog.io
https://ansohxxn.github.io/algorithm/trie/#google_vignette
(C++) 문자열 집합 : 트라이 자료구조
🚀 트라이 자료구조
ansohxxn.github.io
https://github.com/gyoogle/tech-interview-for-developer
GitHub - gyoogle/tech-interview-for-developer: 👶🏻 신입 개발자 전공 지식 & 기술 면접 백과사전 📖
👶🏻 신입 개발자 전공 지식 & 기술 면접 백과사전 📖. Contribute to gyoogle/tech-interview-for-developer development by creating an account on GitHub.
github.com
'CS > Data Structure' 카테고리의 다른 글
| [Data Structure] Hash (0) | 2024.04.03 |
|---|---|
| [Data Structure] B-Tree&B+Tree (0) | 2024.04.03 |
| [Data Structure] Binary Search Tree (1) | 2024.03.31 |
| [Data Structure] Tree (0) | 2024.03.31 |
| [Data Structure] Heap (0) | 2024.03.31 |
