Heap(힙)?
- 데이터에서 최대값과 최소값을 빠르게 찾기 위해 고안된 완전 이진 트리(Complete Binary Tree)
- 힙은, 우선순위 큐를 위해 만들어진 자료구조다.
- 우선순위 큐란 우선순위 개념을 큐에 도입한 자료구조이다.
- 데이터들이 우선순위를 가지고 있어 우선순위가 높은 데이터가 먼저 나가게 된다.

- 반정렬 상태를 유지
- 큰 값이 상위 레벨에 있고 작은 값이 하위 레벨에 있다는 정도
- 간단히 말하면 부모 노드의 키 값이 자식 노드의 키 값보다 항상 큰(작은) 이진 트리를 말한다.
- 힙 트리는 중복된 값을 허용
- 이진 탐색 트리는 중복 값을 허용하지 않음
완전 이진 트리?

- 이진 트리에 노드를 삽입할 때 왼쪽부터 차례대로 삽입하는 트리이다.
- 왼쪽이 비어있고 오른쪽이 채워져 있는 형태는 완전 이진 트리라고 할 수 없다.
힙 종류
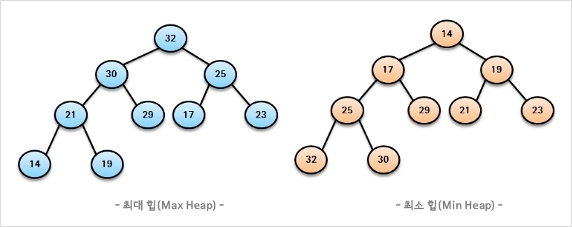
- 최대 힙(Max Heap)
- 부모 노드의 키 값이 자식 노드의 키 값보다 크거나 같은 완전 이진 트리
- key(부모 노드) >= key(자식 노드)
- 최소 힙(Min Heap)
- 부모 노드의 키 값이 자식 노드의 키 값보다 작거나 같은 완전 이진 트리
- key(부모 노드) <= key(자식 노드)
힙을 사용하는 이유?
- 최솟값이나 최댓값을 찾기 위해 배열을 사용하면 Ο(n)만큼 시간이 걸린다.
- 힙을 사용하면 O(logn)만큼 소요되므로, 배열을 사용할 때보다 빠르게 최솟값과 최댓값을 구할 수 있다.
- 우선순위 큐와 같이 최댓값 또는 최솟값을 빠르게 찾아야하는 알고리즘 등에 활용
힙 vs 이진 탐색 트리

공통점
- 모두 완전 이진 트리이다.
차이점
- 힙은 각 노드의 값이 자식 노드보다 크거나 같다.
- 이 점은 최대 힙의 경우 해당한다.
- 이진 탐색 트리는 각 노드의 왼쪽 자식은 더 작은 값으로, 오른쪽 자식은 더 큰 값으로 이루어져있다.
- 힙은 왼쪽 노드의 값이 크든 오른쪽 노드의 값이 크든 상관 없다.
- 힙은 최대/최소 검색을, 이진 탐색 트리는 탐색을 위한 구조이다.
힙 구현
- 힙을 저장하는 표준적인 자료구조는 배열이다.
- 구현을 쉽게 하기 위해 배열의 첫번째 인덱스인 0은 사용되지 않음
- 특정 위치의 노드 번호는 새로운 노드가 추가되어도 변하지 않음
- 예) 루트 노드의 오른쪽 노드 번호는 항상 3
- 부모 노드와 자식 노드와의 관계
- 왼쪽 자식 index = (부모 index) * 2
- 오른쪽 자식 index = (부모 index) * 2 + 1
- 부모 index = 자식 index / 2
힙의 삽입
- 힙은 완전 이진 트리이기 때문에, 삽입할 노드는 기본적으로 왼쪽 최하단부 노드부터 채워진다.
- 채워진 노드의 위치에서, 부모 노드의 값보다 클 경우에는 부모 노드와 위치를 바꾸며 이를 반복한다.
기본 과정
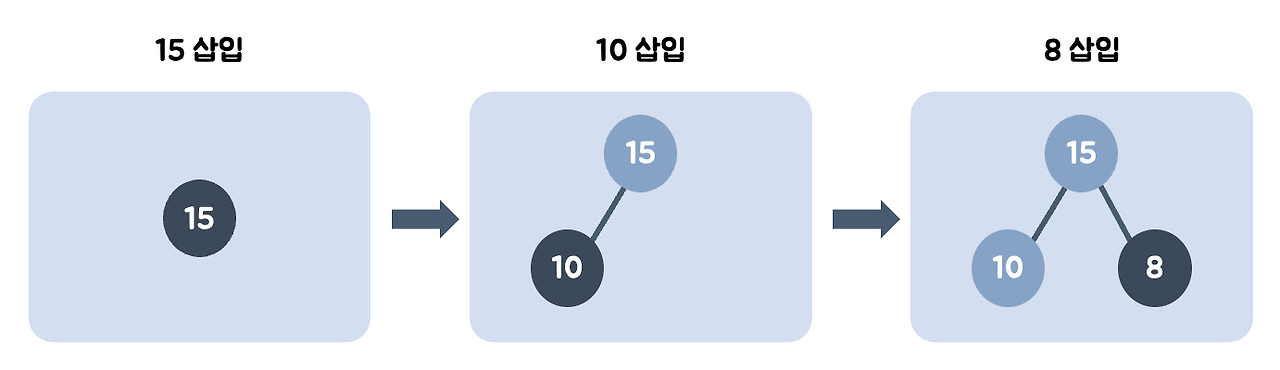
- 15를 왼쪽 최하단 노드에 삽입한다.
- 10을 왼쪽 최하단 노드에 삽입한 뒤, 부모와 비교한다. 부모보다 작으므로 그 자리에 위치한다.
- 왼쪽 최하단 노드가 이미 있으므로 8을 오른쪽 최하단 노드에 삽입한 뒤, 부모와 비교한다. 부모보다 작으므로 그 자리에 위치한다.
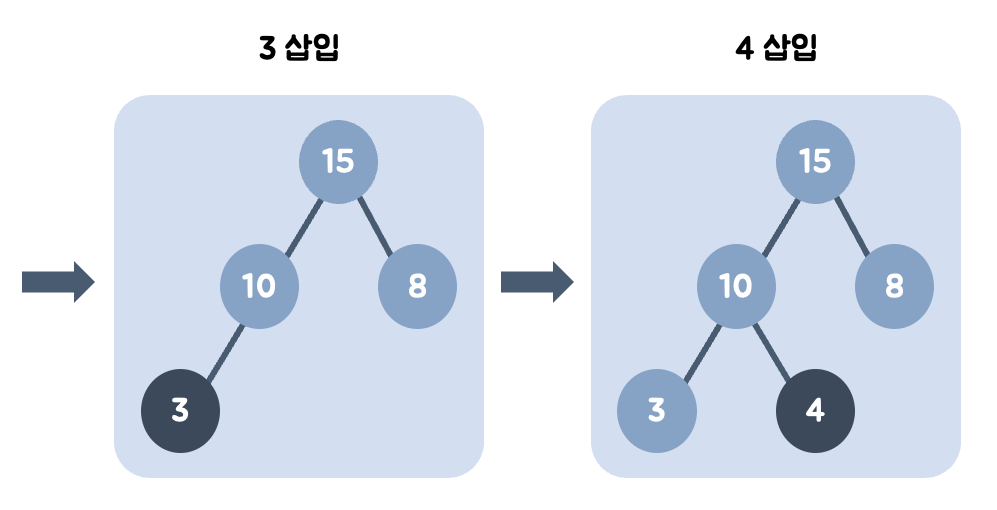
- 3을 왼쪽 최하단 노드에 삽입한 뒤, 부모와 비교한다. 부모보다 작으므로 그 자리에 위치한다.
- 왼쪽 최하단 노드가 이미 있으므로 4를 오른쪽 최하단 노드에 삽입한 뒤, 부모와 비교한다. 부모보다 작으므로 그 자리에 위치한다.
힙에 존재하는 데이터보다 큰 경우


- 20을 왼쪽 최하단부 노드에 삽입한다.
- 20의 부모 노드인 8과 비교한다. 20이 더 크므로 8과 위치를 바꾼다. (swap)
- 20의 부모 노드인 15와 비교한다. 20이 더 크므로 15와 위치를 바꾼다. (swap)
최대 힙 삽입 구현
void insert_max_heap(int x){
heap[++heapSize] = x;
// 힙 크기를 하나 증가하고, 마지막 노드에 x를 넣음
for( int i = heapSize; i > 1; i /= 2) {
// 마지막 노드가 자신의 부모 노드보다 크면 swap
if(heap[i/2] < heap[i]) {
swap(i/2, i);
} else {
break;
}
}
}- 부모 노드는 자신의 인덱스의 /2 이므로, 비교하고 자신이 더 크면 swap하는 방식
힙의 삭제
- 최대 힙에서 최대값은 루트 노드이므로 루트 노드가 삭제됨
- 최대 힙에서 삭제 연산은 최대값 요소를 삭제하는 것
- 삭제된 루트 노드에는 힙의 마지막 노드를 가져옴
- 힙을 재구성하여 구조가 올바르도록 조정한다.
기본 과정

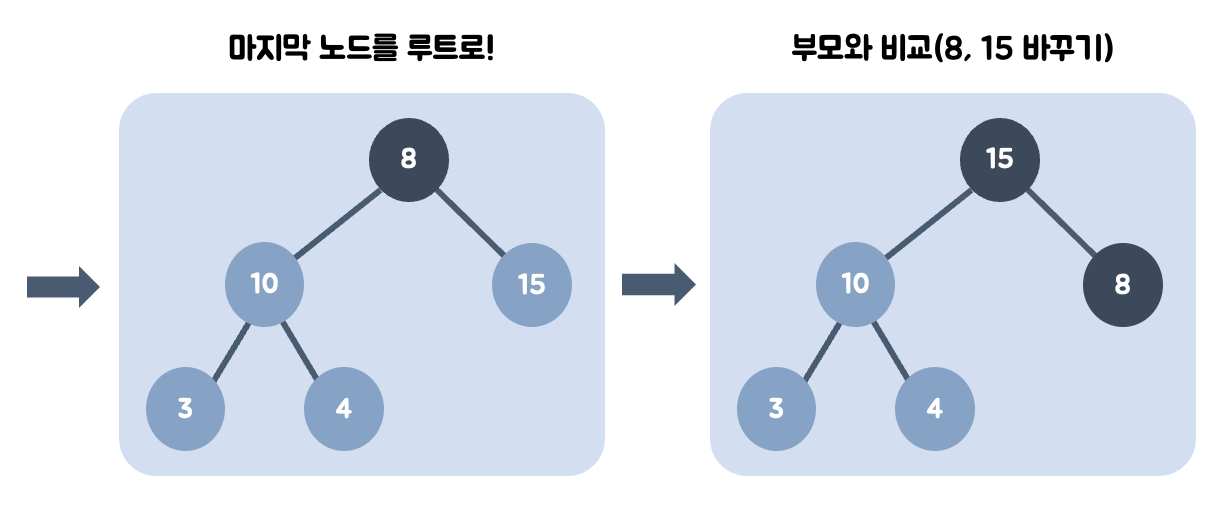
- 최대값을 갖는 부모 노드를 삭제한다.
- 부모 노드가 비었으므로, 가장 최하단부 노드를 루트로 옮긴다.
- 부모 노드인 8보다 값이 큰 자식 노드가 있는지 비교한다.
- 왼쪽, 오른쪽 자식 노드 모두 부모 노드보다 클 경우
- 왼쪽 자식 노드와 오른쪽 자식 노드를 비교하여, 더 큰 자식 노드와 부모 노드의 위치를 바꾼다. (swap)
- 왼쪽, 오른쪽 자식 노드 중 하나만 부모 노드보다 클 경우
- 둘 중에 부모 노드보다 큰 자식 노드와 부모 노드의 위치를 바꾼다. (swap)
- 왼쪽, 오른쪽 자식 노드 모두 부모 노드보다 클 경우
최대 힙 삭제 구현
int delete_max_heap() {
if(heapSize == 0) // 배열이 비어있으면 리턴
return 0;
int item = heap[1]; // 루트 노드의 값을 저장
heap[1] = heap[heapSize]; // 마지막 노드 값을 루트로 이동
heap[heapSize--] = 0; // 힙 크기를 하나 줄이고 마지막 노드 0 초기화
for(int i = 1; i*2 <= heapSize;) {
// 마지막 노드가 왼쪽 노드와 오른쪽 노드보다 크면 끝
if(heap[i] > heap[i*2] && heap[i] > heap[i*2+1]) {
break;
}
// 왼쪽 노드가 더 큰 경우, swap
else if (heap[i*2] > heap[i*2+1]) {
swap(i, i*2);
i = i*2;
}
// 오른쪽 노드가 더 큰 경우
else {
swap(i, i*2+1);
i = i*2+1;
}
}
return item;
}최대 힙 전체 소스 코드
#include <iostream>
using namespace std;
#define MAX_ELEMENT 200
class MaxHeap{
public:
int heap[MAX_ELEMENT];
int heapSize = 0;
void swap(int idx1, int idx2){
int temp = heap[idx1];
heap[idx1] = heap[idx2];
heap[idx2] = temp;
}
void insert_max_heap(int x){
heap[++heapSize] = x;
// 힙 크기를 하나 증가하고, 마지막 노드에 x를 넣음
for( int i = heapSize; i > 1; i /= 2) {
// 마지막 노드가 자신의 부모 노드보다 크면 swap
if(heap[i/2] < heap[i]) {
swap(i/2, i);
} else {
break;
}
}
}
int delete_max_heap() {
if(heapSize == 0) // 배열이 비어있으면 리턴
return 0;
int item = heap[1]; // 루트 노드의 값을 저장
heap[1] = heap[heapSize]; // 마지막 노드 값을 루트로 이동
heap[heapSize--] = 0; // 힙 크기를 하나 줄이고 마지막 노드 0 초기화
for(int i = 1; i*2 <= heapSize;) {
// 마지막 노드가 왼쪽 노드와 오른쪽 노드보다 크면 끝
if(heap[i] > heap[i*2] && heap[i] > heap[i*2+1]) {
break;
}
// 왼쪽 노드가 더 큰 경우, swap
else if (heap[i*2] > heap[i*2+1]) {
swap(i, i*2);
i = i*2;
}
// 오른쪽 노드가 더 큰 경우
else {
swap(i, i*2+1);
i = i*2+1;
}
}
return item;
}
};
int main(){
MaxHeap heap;
heap.insert_max_heap(10);
heap.insert_max_heap(30);
heap.insert_max_heap(50);
heap.insert_max_heap(5);
cout<<heap.delete_max_heap()<<'\n';
}우선순위 큐를 활용한 힙 구현
- C++ 라이브러리인 우선순위 큐를 활용하여 최대 힙과 최소 힙을 구현할 수 있다.
- C++에서는 최대 힙이 기본 값이며 최소 힙을 사용하기 위해서는 비교 연산자를 사용해야한다.
최대 힙 구현
#include <iostream>
#include<queue>
#include<vector>
using namespace std;
priority_queue<int> pQ;
int main() {
pQ.push(2);
pQ.push(6);
pQ.push(5);
pQ.push(1);
pQ.push(4);
pQ.push(3);
for (int i = 1; i <= 6; i++) {
cout << pQ.top() << " ";
pQ.pop();
}
return 0;
}최소 힙 구현
#include <iostream>
#include<queue>
#include<vector>
using namespace std;
priority_queue<int, vector<int>, greater<>> pQ;
int main() {
pQ.push(2);
pQ.push(6);
pQ.push(5);
pQ.push(1);
pQ.push(4);
pQ.push(3);
for (int i = 1; i <= 6; i++) {
cout << pQ.top() << " ";
pQ.pop();
}
return 0;
}
출처
https://velog.io/@gnwjd309/data-structure-heap
[자료구조] 힙(Heap) 이해하기
Heap이란 무엇인가요!
velog.io
우선순위 큐(priority_queue) 최대 힙, 최소 힙 in C++ - (2)
C++ 에서는 최대힙이 디폴트 값이다. 따라서 추가적인ㅇ 조치를 하지 않아도 내림차순으로 출력이 된다.priority_queue<int, vector, greater> pQ; : 최소 힙을 사용하게 하여, 오름차순으로 출력되게 한다.
velog.io
https://gmlwjd9405.github.io/2018/05/10/data-structure-heap.html
'CS > Data Structure' 카테고리의 다른 글
| [Data Structure] Binary Search Tree (1) | 2024.03.31 |
|---|---|
| [Data Structure] Tree (0) | 2024.03.31 |
| [Data Structure] Queue (0) | 2024.03.31 |
| [Data Structure] Stack (0) | 2024.03.31 |
| [Data Structure] Linked List (0) | 2024.03.26 |
