-
Binary Search Tree(이진 탐색 트리)?
-
이진 트리(Binary Tree)?
-
정 이진 트리(Full Binary Tree)
-
완전 이진 트리(Complete Binary Tree)
-
완전 이진 탐색 트리(Complete binary search tree)
-
포화 이진 트리 (Perfect Binary Tree)
-
편향 이진트리(skewed binary tree)
-
균형 이진 트리 (Balanced Binary Tree)
-
높이 균형 이진 탐색 트리 (Adelson-Velsky and Landis, AVL 트리)
-
Red-Black 트리
-
이진 탐색 트리의 핵심 연산
-
탐색
-
삽입
-
삭제
-
전체 소스 코드
Binary Search Tree(이진 탐색 트리)?
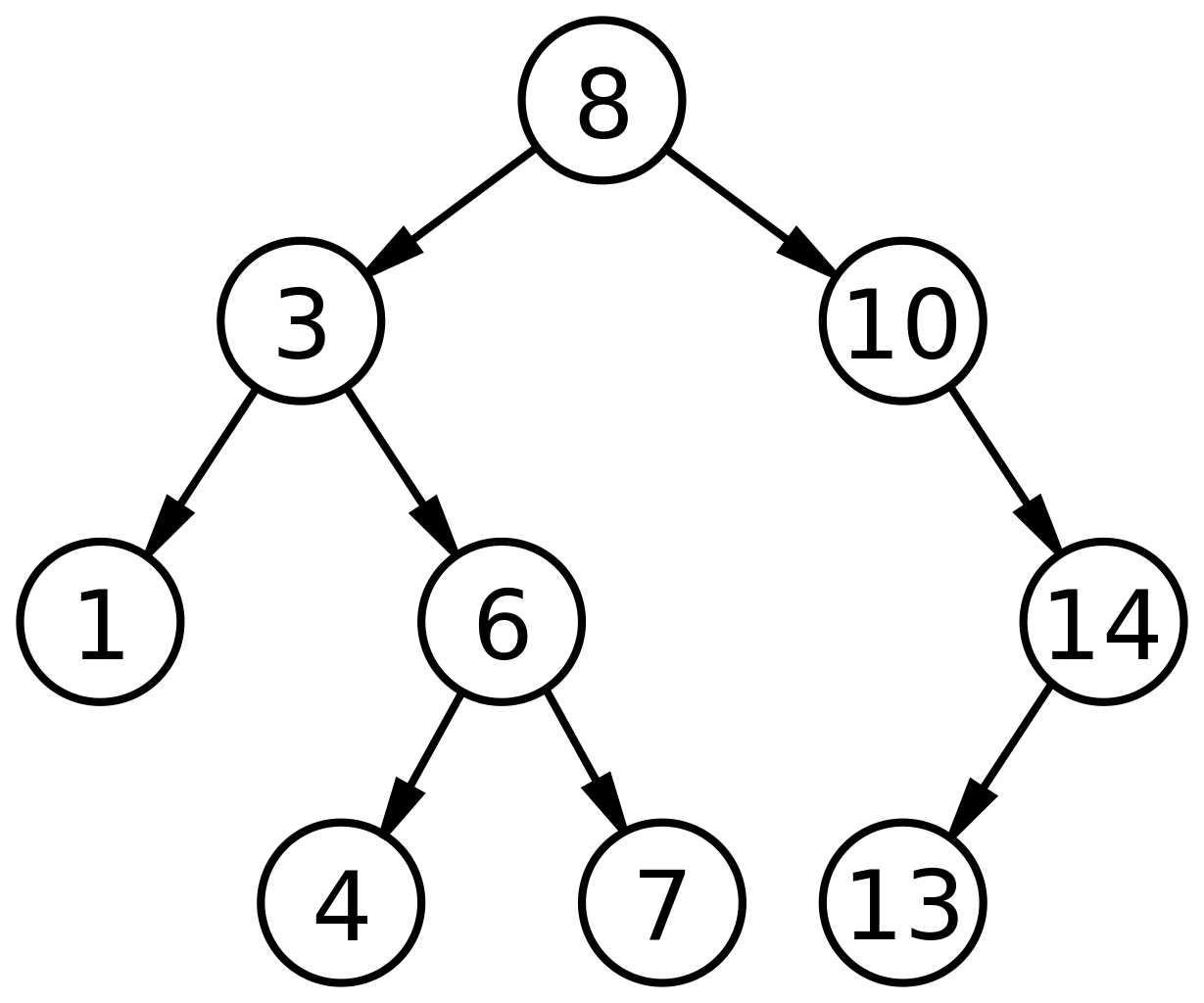
- 왼쪽 자식은 부모보다 작고 오른쪽 자식은 부모보다 큰 이진 트리이다.
- BST는 아래와 같은 조건을 가진다.
- 부모 노드의 왼쪽 노드는 부모 노드보다 작아야 한다.
- 부모 노드의 오른쪽 노드는 부모 노드보다 커야 한다.
- BST는 삽입, 삭제, 탐색과정에서 모두 트리의 높이만큼 탐색하기 때문에 O(logN)의 시간 복잡도를 가진다.
- 트리가 편향트리가 되어버렸을 때 결국 배열과 다름 없어지고 시간 복잡도는 O(N)이 된다.
- 중복된 노드가 존재하지 않는다.
- 검색 목적 자료구조인데, 굳이 중복이 많은 경우에 트리를 사용하여 검색 속도를 느리게 할 필요가 없음
- 트리에 삽입하는 것보다, 노드에 count 값을 가지게 하여 처리하는 것이 훨씬 효율적
- 이진탐색트리의 순회는 중위순회(inorder) 방식
- 왼쪽 - 루트 - 오른쪽
- 중위 순회로 정렬된 순서를 읽을 수 있음
이진 트리(Binary Tree)?
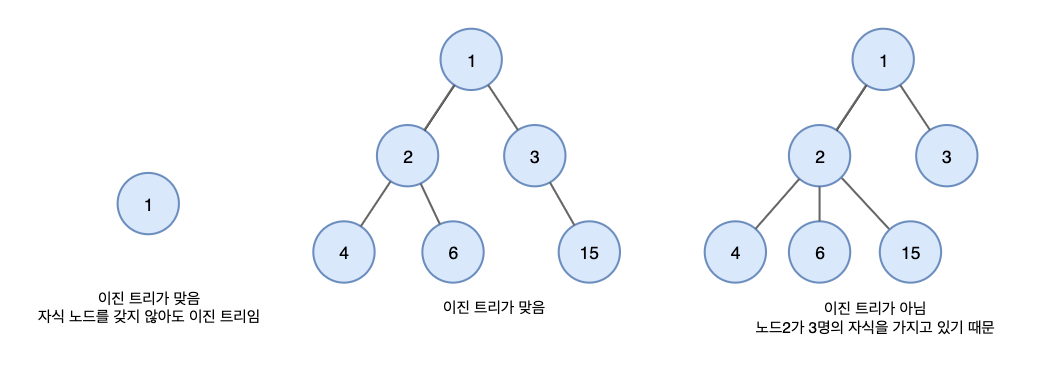
- 모든 노드들이 둘 이하(0,1,2 개)의 자식을 가진 트리이다.
정 이진 트리(Full Binary Tree)
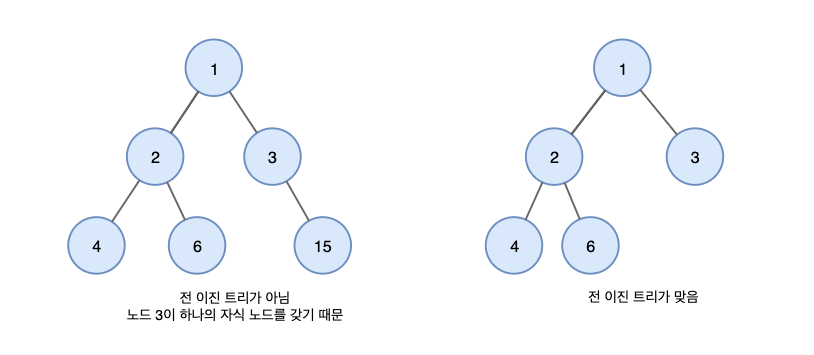
- 모든 노드가 0개 또는 2개의 자식 노드를 갖는 트리이다.
완전 이진 트리(Complete Binary Tree)
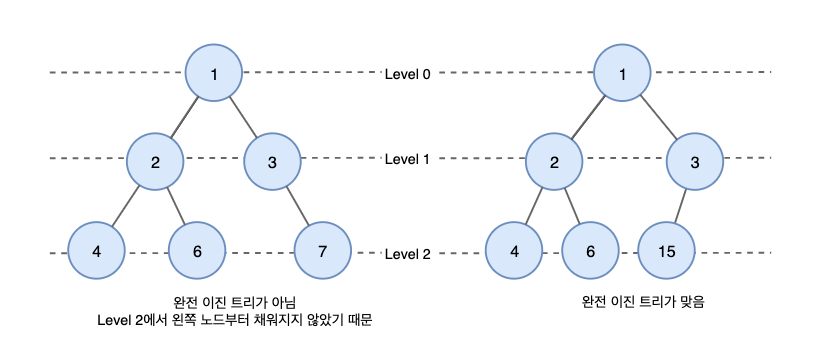
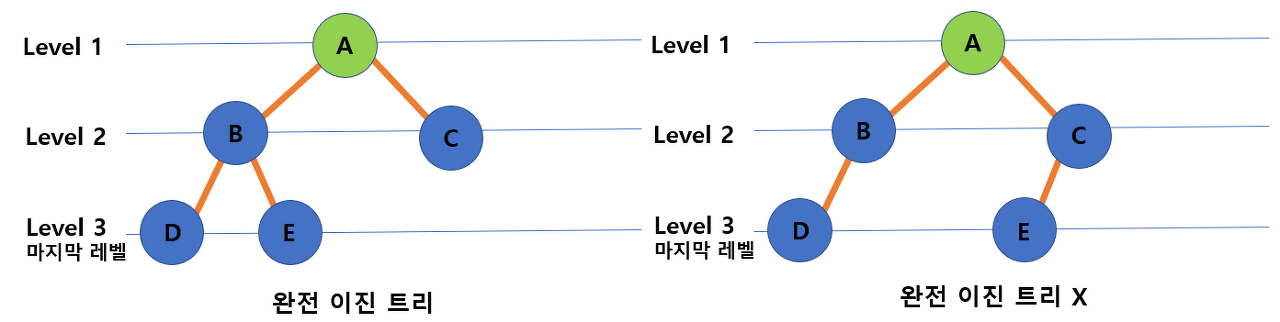
- 마지막 레벨을 제외하고 모든 레벨이 완전히 채워져 있는 트리이다.
- 마지막 레벨은 꽉 차 있지 않아도 되지만 노드가 왼쪽에서 오른쪽으로 채워져야 한다.
- 완전 이진 트리의 개념은 힙(heap)과 관련이 있다.
완전 이진 탐색 트리(Complete binary search tree)
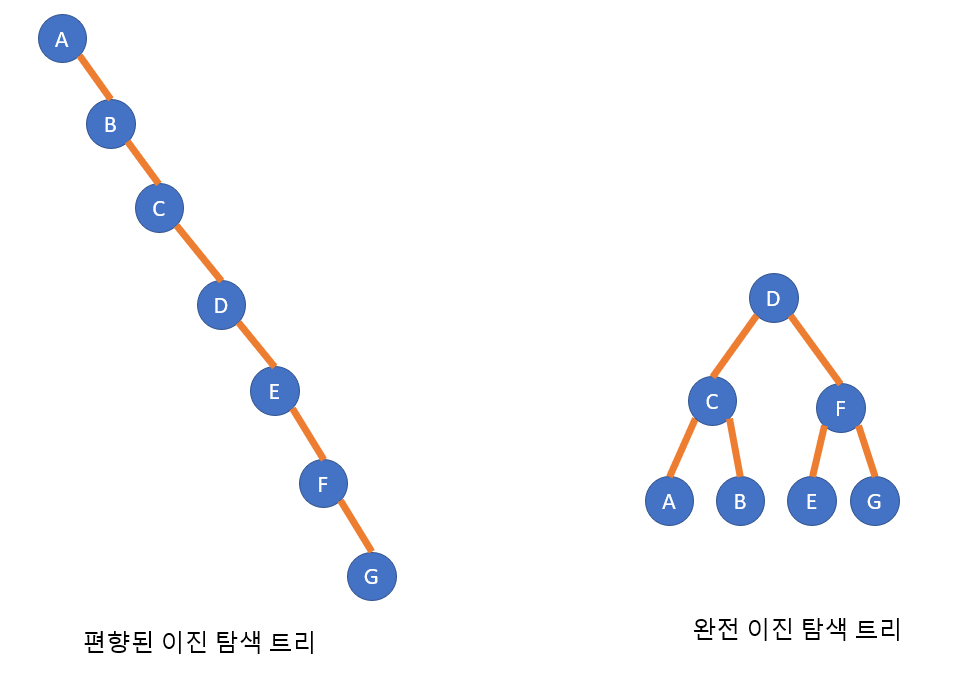
- 완전 이진 트리의 성질을 가지는 이진 탐색 트리이다.
- 편향된 이진 탐색 트리와 다르게 항상 O(log n)의 검색 속도를 보장한다.
- 트리에 자료가 삽입될 때 마다 완전 이진 탐색 트리의 형태를 유지하기 위해 트리의 모양을 바꾸어야 하기 때문에 삽입 시 시간이 많이 소요된다.
- 삽입이 적고 탐색이 많은 경우에 유리
- 삽입하는 빈도수가 높아지면 효율성이 떨어지고 이를 해결한 것이 AVL트리
포화 이진 트리 (Perfect Binary Tree)
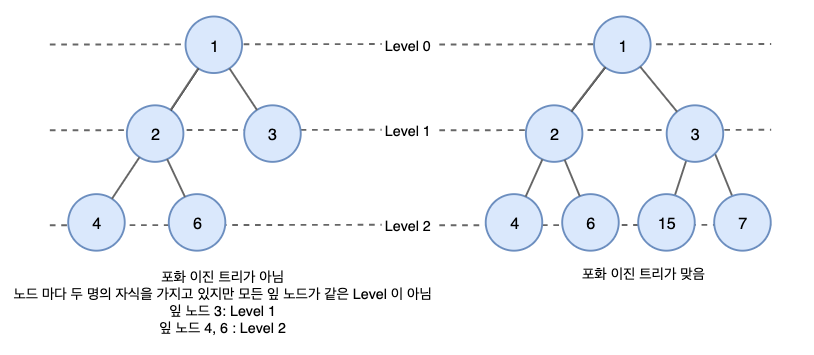
- 정 이진 트리이면서 완전 이진 트리인 경우이다.
- 모든 리프 노드의 레벨이 동일하고, 모든 레벨이 가득 채워져 있는 트리이다.
- 즉, 모든 노드가 두 개의 자식 노드를 가지며 모든 잎 노드가 동일한 깊이 또는 레벨을 갖는다.
편향 이진트리(skewed binary tree)
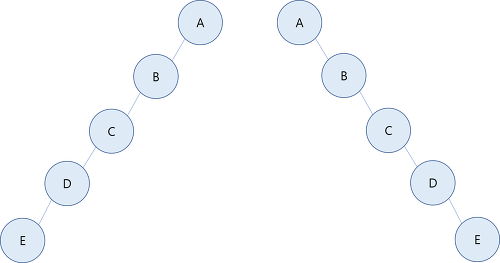
- 같은 높이의 이진 트리 중에서 최소 개수의 노드 개수를 가지면서 왼쪽 혹은 오른쪽 서브트리만을 가지는 이진트리이다.
- 즉, 모든 노드가 왼쪽에 있거나 반대로 오른쪽에 있는 트리이다.
- 각 부모 노드가 오직 한 개의 연관 자식 노드를 갖는 트리이다.
- 사향 이진 트리(Degenerate (or Pathological) Tree) 라고도 부른다.
- Linked List 성능과 동일하다.
균형 이진 트리 (Balanced Binary Tree)
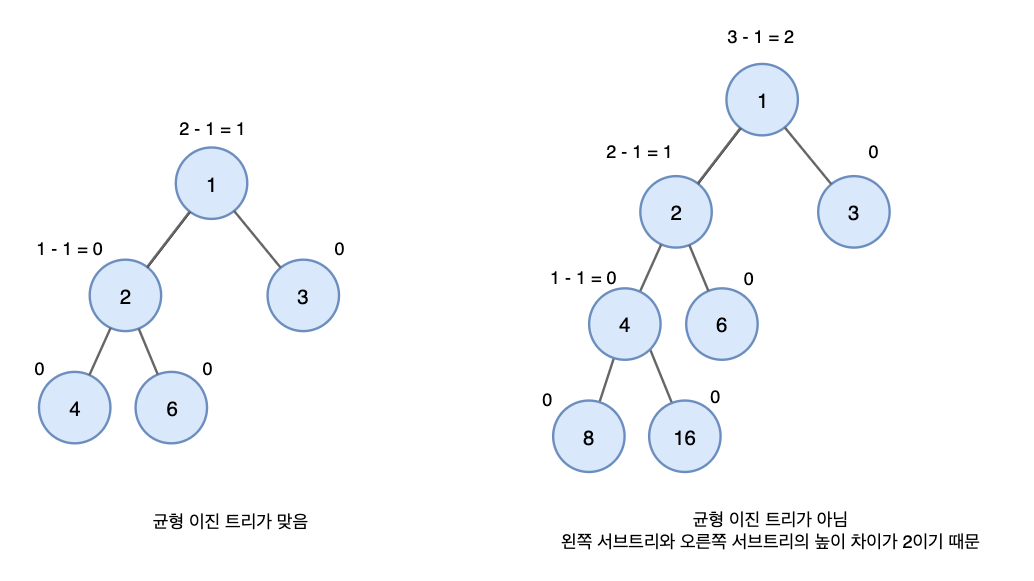
- 높이 균형이 맞춰진 이진트리이다.
- 왼쪽과 오른쪽 트리의 높이 차이가 모두 1만큼 나는 트리이다.
- 예) AVL(높이 균형 이진 탐색 트리)과 Red-Black 트리가 있다.
높이 균형 이진 탐색 트리 (Adelson-Velsky and Landis, AVL 트리)
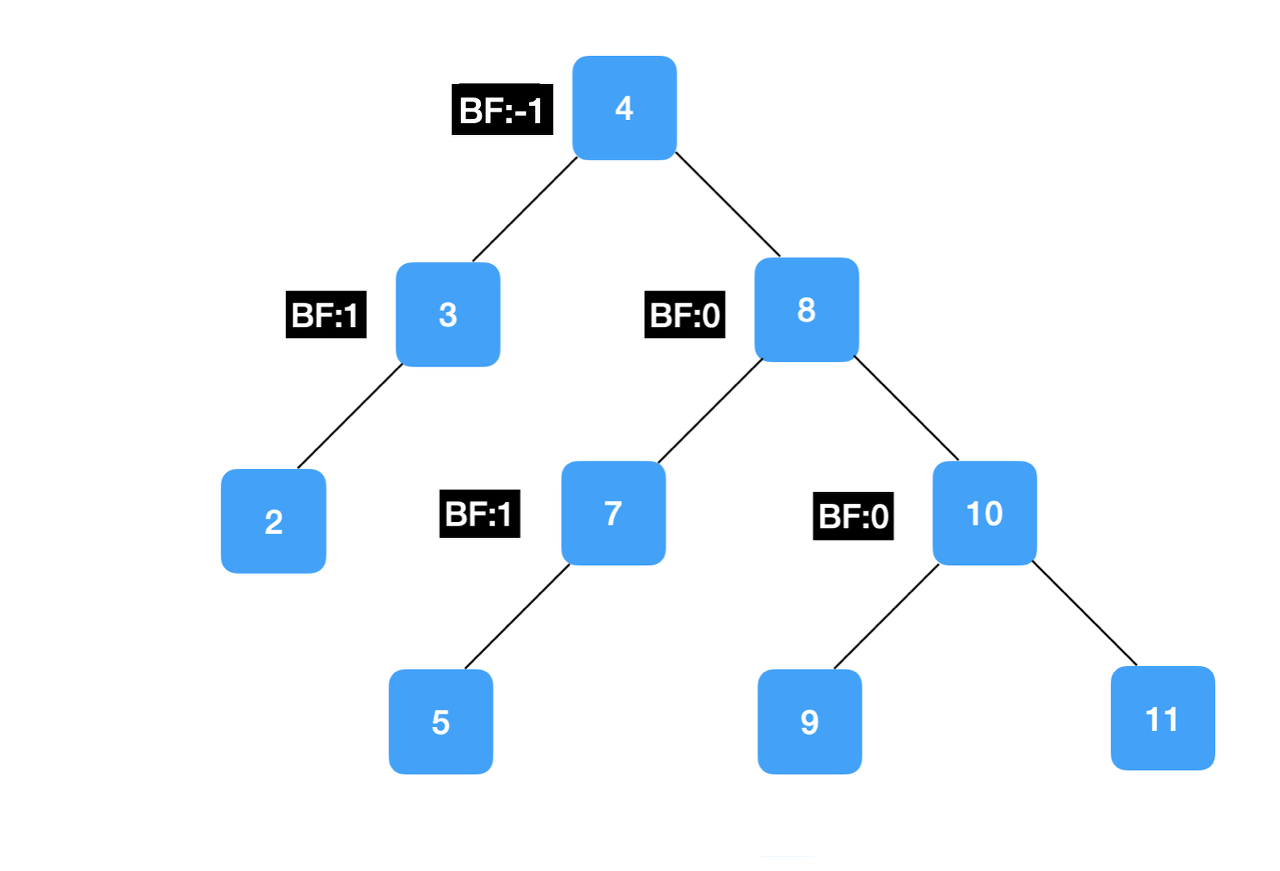
- 스스로 균형을 잡는 이진 탐색 트리이다.
- 균형을 잡을 때 핵심되는 것은 Balance Factor라는 것
- Balance Factor는 왼쪽과 오른쪽의 자식의 높이 차이를 뜻한다.
- 이 때 균형이 잡혔다는 것은 BF가 최대 1까지 차이나는 것
- 즉 -1부터 1까지일 때를 의미한다.
- AVL트리는 삽입, 삭제, 탐색 모두 평균이든 최악의 경우든 O(logN)이다.
- 이진탐색 트리는 삽입, 삭제, 탐색 모두 평균은 O(logN)이지만 최악은 O(N)
- AVL 트리에서 삽입, 삭제 연산을 수행할 때 트리의 균형을 유지하기 위해 LL-회전, RR-회전, LR-회전, RL-회전연산이 사용된다.
Red-Black 트리

- 자가 균형 이진 탐색 트리이다.
- 이진 탐색 트리와 달리 최악의 경우에도 O(log n)의 시간복잡도로 삽입, 삭제, 검색을 할 수 있기 때문에 사용한다.
- 자세한 내용은 이 포스팅을 참고하면 된다.
- AVL 트리는 균형을 엄격하게 유지하는데, red-black tree는 색상이 추가되어 여유롭게 균형을 유지하기 때문에 AVL 트리에 비하여 삽입, 삭제가 빠르다.
이진 탐색 트리의 핵심 연산
탐색
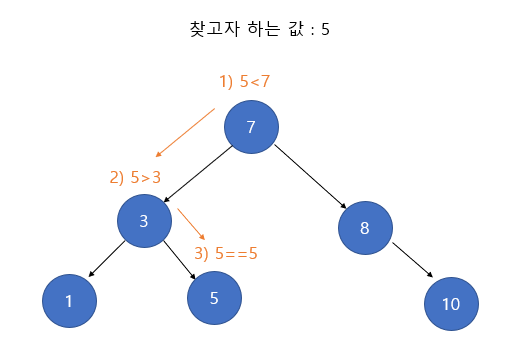
- 이진 탐색 트리의 탐색은 다음과 같은 과정을 거친다.
- 루트 노드의 키와 찾고자 하는 값을 비교한다. 찾고자 하는 값이면 탐색을 종료한다.
- 찾고자 하는 값이 루트 노드의 키보다 작다면, 왼쪽 서브 트리로 탐색을 진행한다.
- 찾고자 하는 값이 루트 노드의 키보다 크다면, 오른쪽 서브 트리로 탐색을 진행한다.
- 만약 탐색에 실패했다면 그대로 종료한다.
- 위 탐색 과정을 거치면 최대 트리 높이(h)만큼 탐색이 진행되게 된다.
탐색 소스 코드
bool search(int key){
Node* current = root;
while(current != NULL){
if(current->data == key)
return true;
else if(current->data>key)
current = current->left;
else
current = current->right;
}
return false;
}- 이진 트리의 탐색의 구현은 반복을 통해 구현할 수 있다.
- 재귀를 통해서도 구현할 수도 있다. 재귀 함수를 통해 구현하는 것이 직관적이다.
삽입
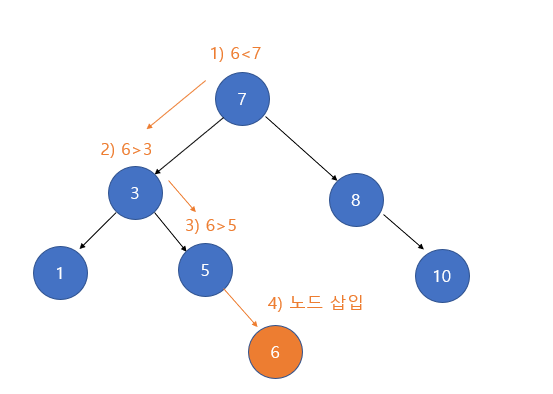
- 이진 탐색 트리의 삽입은 탐색 과정과 유사하게 진행된다.
- 삽입할 값을 루트 노드와 비교해 같다면 오류를 발생한다. (중복 값을 허용하지 않음)
- 삽입할 값이 루트 노드의 키보다 작다면 왼쪽 서브 트리를 탐색해서 비어있다면 추가하고, 비어있지 않다면 다시 값을 비교
- 삽입할 값이 루트 노드의 키보다 크다면 오른쪽 서브 트리를 탐색해서 비어있다면 추가하고, 비어있지 않다면 다시 값을 비교
삽입 소스 코드
void insert(int key) {
Node* newNode = new Node(key);
if (root == NULL) {
root = newNode;
return;
}
Node* current = root;
Node* parent = NULL;
while(true){
parent = current;
if(key < current->data){
current = current->left;
if(current==NULL){
parent->left = newNode;
return;
}
}
else{
current = current->right;
if(current==NULL){
parent->right = newNode;
return;
}
}
}
}- 새로운 노드는 malloc을 통해 동적할당 한다.
- 반복은 노드를 가리키는 포인터가 NULL을 가리키거나 추가를 완료하였다면 종료
삭제
- 이진 탐색 트리에서의 삭제는 삽입보다 조금 더 복잡하다.
- 삭제를 위해서는 3가지 상황을 나누어 구현해야한다.
- 삭제하려는 노드가 단말 노드인 경우 (자식 노드가 없는 경우)
- 삭제하려는 노드의 서브 트리가 하나인 경우 (한 개의 자식만 가지는 경우)
- 삭제하려는 노드의 서브 트리가 두 개인 경우 (두 개의 자식을 가지는 경우)
삭제하려는 노드가 단말 노드인 경우
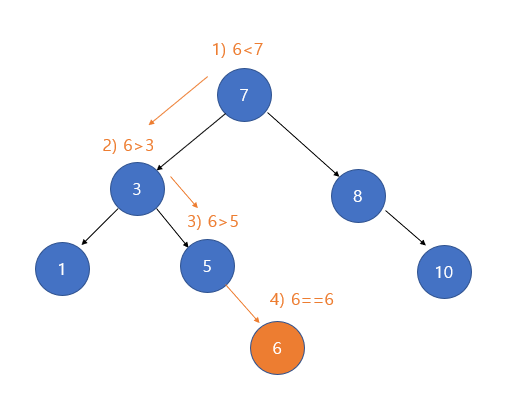 |
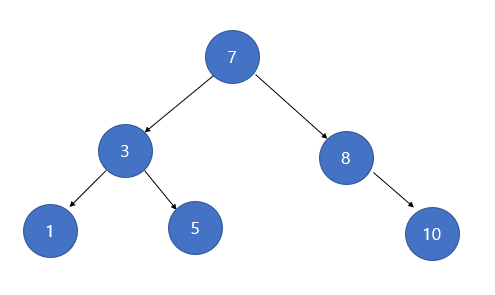 |
- 자식 노드가 없는 경우는 간단하다
- 삭제할 노드의 부모 노드가 있다면 부모 노드의 자식 노드를 NULL로 만들고, 삭제할 노드를 삭제 해주면 된다.
삭제하려는 노드의 서브 트리가 하나인 경우
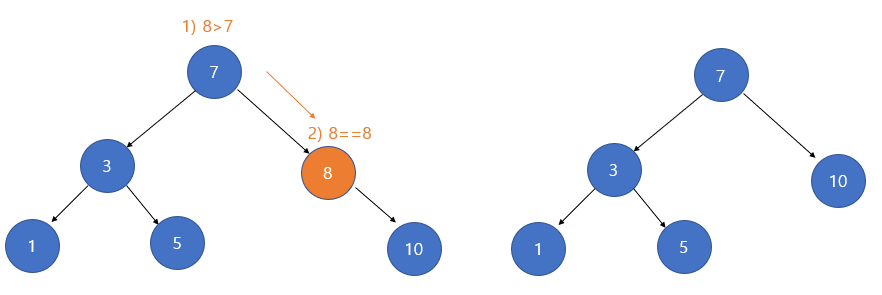
- 삭제하려는 노드의 서브 트리가 하나인 경우도 간단하다.
- 삭제할 노드의 자식노드를 삭제할 노드의 부모노드가 가리키게 하고 해당 노드를 삭제하면 된다.
삭제하려는 노드의 서브트리가 두 개인 경우
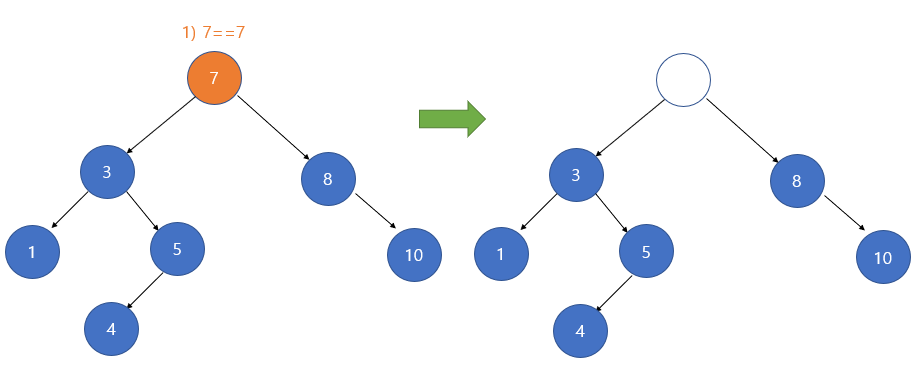
- 삭제하려는 노드의 서브 트리가 두 개인 경우 두 가지 방식을 사용할 수 있다.
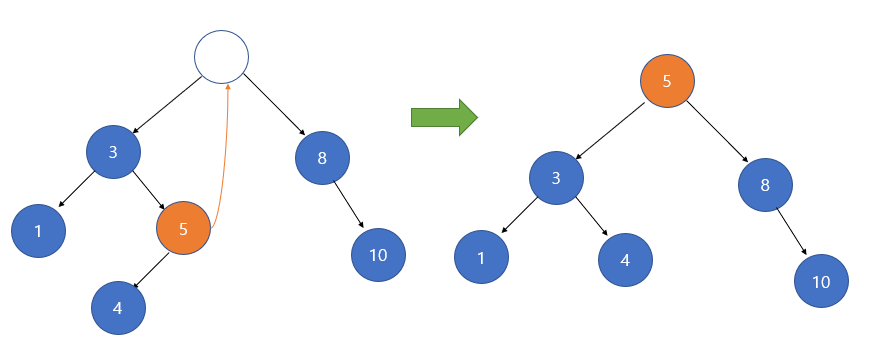
- 첫번째 방식은 삭제할 노드 왼쪽 서브 트리의 가장 큰 자손을 해당 노드의 자리로 옮기는 것이다.
- 삭제할 노드의 왼쪽 서브 트리에서 가장 큰 자손을 해당 노드의 자리에 올리면, 이진 탐색 트리의 조건을 만족하면서 트리가 유지되는 것을 확인할 수 있다.
- 자리를 옮기면서 다른 노드들(4번노드)도 자리가 적절히 이동한 것을 확인 할 수 있다.
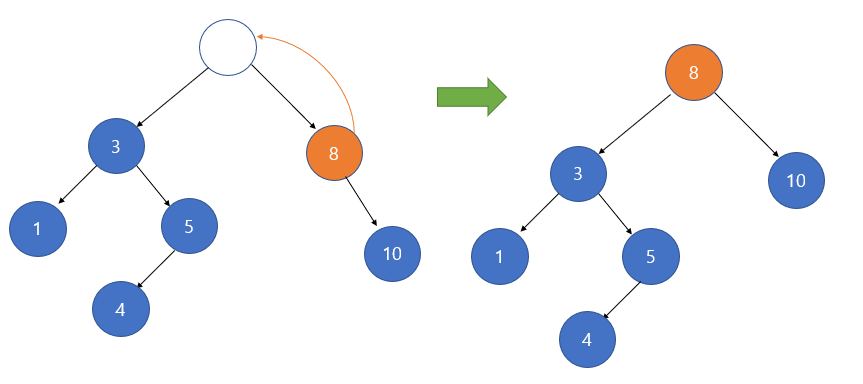
- 두번째 방식은 삭제할 노드 오른쪽 서브 트리의 가장 작은 자손을 해당 노드의 자리에 올리는 것이다.
삭제 소스 코드
bool deleteNode(int key){
Node* parent = root;
Node* current = root;
bool isLeft = false;
while(current->data != key){
parent = current;
if(current->data > key){
isLeft = true;
current = current->left;
}
else{
isLeft = false;
current = current->right;
}
}
// 자식 노드가 없는 경우
if(current->left == NULL && current->right == NULL){
if(current == root)
root = NULL;
if(isLeft == true)
parent->left = NULL;
else
parent->right = NULL;
}
// 하나의 자식을 갖는 경우
else if(current->right == NULL){
if(current==root)
root = current->left;
else if(isLeft)
parent->left = current->left;
else
parent->right = current->left;
}
else if(current->left == NULL){
if(current==root)
root = current->right;
else if(isLeft)
parent->left = current->right;
else
parent->right = current->right;
}
// 두개의 자식을 갖는 경우
else if(current->left != NULL && current->right != NULL){
// 오른쪽 서브트리의 최소 값을 찾음
Node* minNode = getMinNode(current);
if(current==root)
root = minNode;
else if(isLeft)
parent->left = minNode;
else
parent->right = minNode;
minNode->left = current->left;
}
delete current;
return true;
}전체 소스 코드
#include<iostream>
using namespace std;
class Node {
public:
int data;
Node* left;
Node* right;
Node(int data){
this->data = data;
left = NULL;
right = NULL;
}
};
class BinarySearchTree {
public:
Node* root;
BinarySearchTree() {
root = NULL;
}
// 삽입 연산
void insert(int key) {
Node* newNode = new Node(key);
if (root == NULL) {
root = newNode;
return;
}
Node* current = root;
Node* parent = NULL;
while(true){
parent = current;
if(key < current->data){
current = current->left;
if(current==NULL){
parent->left = newNode;
return;
}
}
else{
current = current->right;
if(current==NULL){
parent->right = newNode;
return;
}
}
}
}
// 탐색 연산
bool search(int key){
Node* current = root;
while(current != NULL){
if(current->data == key)
return true;
else if(current->data>key)
current = current->left;
else
current = current->right;
}
return false;
}
// 삭제 연산
bool deleteNode(int key){
Node* parent = root;
Node* current = root;
bool isLeft = false;
while(current->data != key){
parent = current;
if(current->data > key){
isLeft = true;
current = current->left;
}
else{
isLeft = false;
current = current->right;
}
}
// 자식 노드가 없는 경우
if(current->left == NULL && current->right == NULL){
if(current == root)
root = NULL;
if(isLeft == true)
parent->left = NULL;
else
parent->right = NULL;
}
// 하나의 자식을 갖는 경우
else if(current->right == NULL){
if(current==root)
root = current->left;
else if(isLeft)
parent->left = current->left;
else
parent->right = current->left;
}
else if(current->left == NULL){
if(current==root)
root = current->right;
else if(isLeft)
parent->left = current->right;
else
parent->right = current->right;
}
// 두개의 자식을 갖는 경우
else if(current->left != NULL && current->right != NULL){
// 오른쪽 서브트리의 최소 값을 찾음
Node* minNode = getMinNode(current);
if(current==root)
root = minNode;
else if(isLeft)
parent->left = minNode;
else
parent->right = minNode;
minNode->left = current->left;
}
delete current;
return true;
}
Node* getMinNode(Node* deleteNode){
Node* minNode = NULL;
Node* minParent = NULL;
Node* current = deleteNode->right;
while(current!=NULL){
minParent = minNode;
minNode = current;
current = current->left;
}
if(minNode!=deleteNode->right){
minParent->left = minNode->right;
minNode->right = deleteNode->right;
}
return minNode;
}
void display(Node* root){
if(root!=NULL){
display(root->left);
cout<<" "<<root->data;
display(root->right);
}
}
};
int main() {
BinarySearchTree* bst=new BinarySearchTree();
bst->insert(3); bst->insert(8);
bst->insert(1); bst->insert(4); bst->insert(6);
bst->insert(2); bst->insert(10);
bst->insert(9); bst->insert(20);
bst->insert(25); bst->insert(15); bst->insert(16);
cout<<"트리삽입 결과 : ";
bst->display(bst->root);
cout << '\n';
cout<<"이진 트리에서 4를 탐색 "<<bst->search(4)<<'\n';
cout<<"이진 트리에서 2를 삭제"<<bst->deleteNode(2)<<'\n';
bst->display(bst->root);
cout<<"\n이진트리에서 4를 삭제"<<bst->deleteNode(4)<<'\n';
bst->display(bst->root);
cout<<"\n이진트리에서 10을 삭제"<<bst->deleteNode(10)<<'\n';
bst->display(bst->root);
}
// 결과
트리삽입 결과 : 1 2 3 4 6 8 9 10 15 16 20 25
이진 트리에서 4를 탐색 1
이진 트리에서 2를 삭제1
1 3 4 6 8 9 10 15 16 20 25
이진트리에서 4를 삭제1
1 3 6 8 9 10 15 16 20 25
이진트리에서 10을 삭제1
1 3 6 8 9 15 16 20 25%
출처
[CS - 자료구조] 이진 트리 (Binary Tree) 개념과 종류
이것도 면접 질문으로 받았었다. 바이너리 트리에 대해서 배우기는 했지만 종류 같은 것들이 대강은 기억나지만 디테일 하게 기억이 나지 않았다. 그래서 풀 바이너리 트리 물어보는데 컴플릿
velog.io
https://code-lab1.tistory.com/10
[자료구조] 이진탐색트리(Binary Search Tree)의 개념, 이해 | C언어 이진탐색트리 구현
이진탐색트리(Binary Search Tree)이란? 이진탐색트리란 다음과 같은 특징을 갖는 이진트리를 말한다. ( #이진트리 - 각 노드의 자식 노드가 최대 2개인 트리) 1. 각 노드에 중복되지 않는 키(key)가 있다
code-lab1.tistory.com
https://github.com/gyoogle/tech-interview-for-developer/tree/master
GitHub - gyoogle/tech-interview-for-developer: 👶🏻 신입 개발자 전공 지식 & 기술 면접 백과사전 📖
👶🏻 신입 개발자 전공 지식 & 기술 면접 백과사전 📖. Contribute to gyoogle/tech-interview-for-developer development by creating an account on GitHub.
github.com
'CS > Data Structure' 카테고리의 다른 글
| [Data Structure] Hash (0) | 2024.04.03 |
|---|---|
| [Data Structure] B-Tree&B+Tree (0) | 2024.04.03 |
| [Data Structure] Tree (0) | 2024.03.31 |
| [Data Structure] Heap (0) | 2024.03.31 |
| [Data Structure] Queue (0) | 2024.03.31 |
Binary Search Tree(이진 탐색 트리)?

- 왼쪽 자식은 부모보다 작고 오른쪽 자식은 부모보다 큰 이진 트리이다.
- BST는 아래와 같은 조건을 가진다.
- 부모 노드의 왼쪽 노드는 부모 노드보다 작아야 한다.
- 부모 노드의 오른쪽 노드는 부모 노드보다 커야 한다.
- BST는 삽입, 삭제, 탐색과정에서 모두 트리의 높이만큼 탐색하기 때문에 O(logN)의 시간 복잡도를 가진다.
- 트리가 편향트리가 되어버렸을 때 결국 배열과 다름 없어지고 시간 복잡도는 O(N)이 된다.
- 중복된 노드가 존재하지 않는다.
- 검색 목적 자료구조인데, 굳이 중복이 많은 경우에 트리를 사용하여 검색 속도를 느리게 할 필요가 없음
- 트리에 삽입하는 것보다, 노드에 count 값을 가지게 하여 처리하는 것이 훨씬 효율적
- 이진탐색트리의 순회는 중위순회(inorder) 방식
- 왼쪽 - 루트 - 오른쪽
- 중위 순회로 정렬된 순서를 읽을 수 있음
이진 트리(Binary Tree)?

- 모든 노드들이 둘 이하(0,1,2 개)의 자식을 가진 트리이다.
정 이진 트리(Full Binary Tree)

- 모든 노드가 0개 또는 2개의 자식 노드를 갖는 트리이다.
완전 이진 트리(Complete Binary Tree)


- 마지막 레벨을 제외하고 모든 레벨이 완전히 채워져 있는 트리이다.
- 마지막 레벨은 꽉 차 있지 않아도 되지만 노드가 왼쪽에서 오른쪽으로 채워져야 한다.
- 완전 이진 트리의 개념은 힙(heap)과 관련이 있다.
완전 이진 탐색 트리(Complete binary search tree)

- 완전 이진 트리의 성질을 가지는 이진 탐색 트리이다.
- 편향된 이진 탐색 트리와 다르게 항상 O(log n)의 검색 속도를 보장한다.
- 트리에 자료가 삽입될 때 마다 완전 이진 탐색 트리의 형태를 유지하기 위해 트리의 모양을 바꾸어야 하기 때문에 삽입 시 시간이 많이 소요된다.
- 삽입이 적고 탐색이 많은 경우에 유리
- 삽입하는 빈도수가 높아지면 효율성이 떨어지고 이를 해결한 것이 AVL트리
포화 이진 트리 (Perfect Binary Tree)

- 정 이진 트리이면서 완전 이진 트리인 경우이다.
- 모든 리프 노드의 레벨이 동일하고, 모든 레벨이 가득 채워져 있는 트리이다.
- 즉, 모든 노드가 두 개의 자식 노드를 가지며 모든 잎 노드가 동일한 깊이 또는 레벨을 갖는다.
편향 이진트리(skewed binary tree)

- 같은 높이의 이진 트리 중에서 최소 개수의 노드 개수를 가지면서 왼쪽 혹은 오른쪽 서브트리만을 가지는 이진트리이다.
- 즉, 모든 노드가 왼쪽에 있거나 반대로 오른쪽에 있는 트리이다.
- 각 부모 노드가 오직 한 개의 연관 자식 노드를 갖는 트리이다.
- 사향 이진 트리(Degenerate (or Pathological) Tree) 라고도 부른다.
- Linked List 성능과 동일하다.
균형 이진 트리 (Balanced Binary Tree)

- 높이 균형이 맞춰진 이진트리이다.
- 왼쪽과 오른쪽 트리의 높이 차이가 모두 1만큼 나는 트리이다.
- 예) AVL(높이 균형 이진 탐색 트리)과 Red-Black 트리가 있다.
높이 균형 이진 탐색 트리 (Adelson-Velsky and Landis, AVL 트리)

- 스스로 균형을 잡는 이진 탐색 트리이다.
- 균형을 잡을 때 핵심되는 것은 Balance Factor라는 것
- Balance Factor는 왼쪽과 오른쪽의 자식의 높이 차이를 뜻한다.
- 이 때 균형이 잡혔다는 것은 BF가 최대 1까지 차이나는 것
- 즉 -1부터 1까지일 때를 의미한다.
- AVL트리는 삽입, 삭제, 탐색 모두 평균이든 최악의 경우든 O(logN)이다.
- 이진탐색 트리는 삽입, 삭제, 탐색 모두 평균은 O(logN)이지만 최악은 O(N)
- AVL 트리에서 삽입, 삭제 연산을 수행할 때 트리의 균형을 유지하기 위해 LL-회전, RR-회전, LR-회전, RL-회전연산이 사용된다.
Red-Black 트리

- 자가 균형 이진 탐색 트리이다.
- 이진 탐색 트리와 달리 최악의 경우에도 O(log n)의 시간복잡도로 삽입, 삭제, 검색을 할 수 있기 때문에 사용한다.
- 자세한 내용은 이 포스팅을 참고하면 된다.
- AVL 트리는 균형을 엄격하게 유지하는데, red-black tree는 색상이 추가되어 여유롭게 균형을 유지하기 때문에 AVL 트리에 비하여 삽입, 삭제가 빠르다.
이진 탐색 트리의 핵심 연산
탐색

- 이진 탐색 트리의 탐색은 다음과 같은 과정을 거친다.
- 루트 노드의 키와 찾고자 하는 값을 비교한다. 찾고자 하는 값이면 탐색을 종료한다.
- 찾고자 하는 값이 루트 노드의 키보다 작다면, 왼쪽 서브 트리로 탐색을 진행한다.
- 찾고자 하는 값이 루트 노드의 키보다 크다면, 오른쪽 서브 트리로 탐색을 진행한다.
- 만약 탐색에 실패했다면 그대로 종료한다.
- 위 탐색 과정을 거치면 최대 트리 높이(h)만큼 탐색이 진행되게 된다.
탐색 소스 코드
bool search(int key){
Node* current = root;
while(current != NULL){
if(current->data == key)
return true;
else if(current->data>key)
current = current->left;
else
current = current->right;
}
return false;
}- 이진 트리의 탐색의 구현은 반복을 통해 구현할 수 있다.
- 재귀를 통해서도 구현할 수도 있다. 재귀 함수를 통해 구현하는 것이 직관적이다.
삽입

- 이진 탐색 트리의 삽입은 탐색 과정과 유사하게 진행된다.
- 삽입할 값을 루트 노드와 비교해 같다면 오류를 발생한다. (중복 값을 허용하지 않음)
- 삽입할 값이 루트 노드의 키보다 작다면 왼쪽 서브 트리를 탐색해서 비어있다면 추가하고, 비어있지 않다면 다시 값을 비교
- 삽입할 값이 루트 노드의 키보다 크다면 오른쪽 서브 트리를 탐색해서 비어있다면 추가하고, 비어있지 않다면 다시 값을 비교
삽입 소스 코드
void insert(int key) {
Node* newNode = new Node(key);
if (root == NULL) {
root = newNode;
return;
}
Node* current = root;
Node* parent = NULL;
while(true){
parent = current;
if(key < current->data){
current = current->left;
if(current==NULL){
parent->left = newNode;
return;
}
}
else{
current = current->right;
if(current==NULL){
parent->right = newNode;
return;
}
}
}
}- 새로운 노드는 malloc을 통해 동적할당 한다.
- 반복은 노드를 가리키는 포인터가 NULL을 가리키거나 추가를 완료하였다면 종료
삭제
- 이진 탐색 트리에서의 삭제는 삽입보다 조금 더 복잡하다.
- 삭제를 위해서는 3가지 상황을 나누어 구현해야한다.
- 삭제하려는 노드가 단말 노드인 경우 (자식 노드가 없는 경우)
- 삭제하려는 노드의 서브 트리가 하나인 경우 (한 개의 자식만 가지는 경우)
- 삭제하려는 노드의 서브 트리가 두 개인 경우 (두 개의 자식을 가지는 경우)
삭제하려는 노드가 단말 노드인 경우
 |
 |
- 자식 노드가 없는 경우는 간단하다
- 삭제할 노드의 부모 노드가 있다면 부모 노드의 자식 노드를 NULL로 만들고, 삭제할 노드를 삭제 해주면 된다.
삭제하려는 노드의 서브 트리가 하나인 경우

- 삭제하려는 노드의 서브 트리가 하나인 경우도 간단하다.
- 삭제할 노드의 자식노드를 삭제할 노드의 부모노드가 가리키게 하고 해당 노드를 삭제하면 된다.
삭제하려는 노드의 서브트리가 두 개인 경우

- 삭제하려는 노드의 서브 트리가 두 개인 경우 두 가지 방식을 사용할 수 있다.

- 첫번째 방식은 삭제할 노드 왼쪽 서브 트리의 가장 큰 자손을 해당 노드의 자리로 옮기는 것이다.
- 삭제할 노드의 왼쪽 서브 트리에서 가장 큰 자손을 해당 노드의 자리에 올리면, 이진 탐색 트리의 조건을 만족하면서 트리가 유지되는 것을 확인할 수 있다.
- 자리를 옮기면서 다른 노드들(4번노드)도 자리가 적절히 이동한 것을 확인 할 수 있다.

- 두번째 방식은 삭제할 노드 오른쪽 서브 트리의 가장 작은 자손을 해당 노드의 자리에 올리는 것이다.
삭제 소스 코드
bool deleteNode(int key){
Node* parent = root;
Node* current = root;
bool isLeft = false;
while(current->data != key){
parent = current;
if(current->data > key){
isLeft = true;
current = current->left;
}
else{
isLeft = false;
current = current->right;
}
}
// 자식 노드가 없는 경우
if(current->left == NULL && current->right == NULL){
if(current == root)
root = NULL;
if(isLeft == true)
parent->left = NULL;
else
parent->right = NULL;
}
// 하나의 자식을 갖는 경우
else if(current->right == NULL){
if(current==root)
root = current->left;
else if(isLeft)
parent->left = current->left;
else
parent->right = current->left;
}
else if(current->left == NULL){
if(current==root)
root = current->right;
else if(isLeft)
parent->left = current->right;
else
parent->right = current->right;
}
// 두개의 자식을 갖는 경우
else if(current->left != NULL && current->right != NULL){
// 오른쪽 서브트리의 최소 값을 찾음
Node* minNode = getMinNode(current);
if(current==root)
root = minNode;
else if(isLeft)
parent->left = minNode;
else
parent->right = minNode;
minNode->left = current->left;
}
delete current;
return true;
}전체 소스 코드
#include<iostream>
using namespace std;
class Node {
public:
int data;
Node* left;
Node* right;
Node(int data){
this->data = data;
left = NULL;
right = NULL;
}
};
class BinarySearchTree {
public:
Node* root;
BinarySearchTree() {
root = NULL;
}
// 삽입 연산
void insert(int key) {
Node* newNode = new Node(key);
if (root == NULL) {
root = newNode;
return;
}
Node* current = root;
Node* parent = NULL;
while(true){
parent = current;
if(key < current->data){
current = current->left;
if(current==NULL){
parent->left = newNode;
return;
}
}
else{
current = current->right;
if(current==NULL){
parent->right = newNode;
return;
}
}
}
}
// 탐색 연산
bool search(int key){
Node* current = root;
while(current != NULL){
if(current->data == key)
return true;
else if(current->data>key)
current = current->left;
else
current = current->right;
}
return false;
}
// 삭제 연산
bool deleteNode(int key){
Node* parent = root;
Node* current = root;
bool isLeft = false;
while(current->data != key){
parent = current;
if(current->data > key){
isLeft = true;
current = current->left;
}
else{
isLeft = false;
current = current->right;
}
}
// 자식 노드가 없는 경우
if(current->left == NULL && current->right == NULL){
if(current == root)
root = NULL;
if(isLeft == true)
parent->left = NULL;
else
parent->right = NULL;
}
// 하나의 자식을 갖는 경우
else if(current->right == NULL){
if(current==root)
root = current->left;
else if(isLeft)
parent->left = current->left;
else
parent->right = current->left;
}
else if(current->left == NULL){
if(current==root)
root = current->right;
else if(isLeft)
parent->left = current->right;
else
parent->right = current->right;
}
// 두개의 자식을 갖는 경우
else if(current->left != NULL && current->right != NULL){
// 오른쪽 서브트리의 최소 값을 찾음
Node* minNode = getMinNode(current);
if(current==root)
root = minNode;
else if(isLeft)
parent->left = minNode;
else
parent->right = minNode;
minNode->left = current->left;
}
delete current;
return true;
}
Node* getMinNode(Node* deleteNode){
Node* minNode = NULL;
Node* minParent = NULL;
Node* current = deleteNode->right;
while(current!=NULL){
minParent = minNode;
minNode = current;
current = current->left;
}
if(minNode!=deleteNode->right){
minParent->left = minNode->right;
minNode->right = deleteNode->right;
}
return minNode;
}
void display(Node* root){
if(root!=NULL){
display(root->left);
cout<<" "<<root->data;
display(root->right);
}
}
};
int main() {
BinarySearchTree* bst=new BinarySearchTree();
bst->insert(3); bst->insert(8);
bst->insert(1); bst->insert(4); bst->insert(6);
bst->insert(2); bst->insert(10);
bst->insert(9); bst->insert(20);
bst->insert(25); bst->insert(15); bst->insert(16);
cout<<"트리삽입 결과 : ";
bst->display(bst->root);
cout << '\n';
cout<<"이진 트리에서 4를 탐색 "<<bst->search(4)<<'\n';
cout<<"이진 트리에서 2를 삭제"<<bst->deleteNode(2)<<'\n';
bst->display(bst->root);
cout<<"\n이진트리에서 4를 삭제"<<bst->deleteNode(4)<<'\n';
bst->display(bst->root);
cout<<"\n이진트리에서 10을 삭제"<<bst->deleteNode(10)<<'\n';
bst->display(bst->root);
}
// 결과
트리삽입 결과 : 1 2 3 4 6 8 9 10 15 16 20 25
이진 트리에서 4를 탐색 1
이진 트리에서 2를 삭제1
1 3 4 6 8 9 10 15 16 20 25
이진트리에서 4를 삭제1
1 3 6 8 9 10 15 16 20 25
이진트리에서 10을 삭제1
1 3 6 8 9 15 16 20 25%
출처
[CS - 자료구조] 이진 트리 (Binary Tree) 개념과 종류
이것도 면접 질문으로 받았었다. 바이너리 트리에 대해서 배우기는 했지만 종류 같은 것들이 대강은 기억나지만 디테일 하게 기억이 나지 않았다. 그래서 풀 바이너리 트리 물어보는데 컴플릿
velog.io
https://code-lab1.tistory.com/10
[자료구조] 이진탐색트리(Binary Search Tree)의 개념, 이해 | C언어 이진탐색트리 구현
이진탐색트리(Binary Search Tree)이란? 이진탐색트리란 다음과 같은 특징을 갖는 이진트리를 말한다. ( #이진트리 - 각 노드의 자식 노드가 최대 2개인 트리) 1. 각 노드에 중복되지 않는 키(key)가 있다
code-lab1.tistory.com
https://github.com/gyoogle/tech-interview-for-developer/tree/master
GitHub - gyoogle/tech-interview-for-developer: 👶🏻 신입 개발자 전공 지식 & 기술 면접 백과사전 📖
👶🏻 신입 개발자 전공 지식 & 기술 면접 백과사전 📖. Contribute to gyoogle/tech-interview-for-developer development by creating an account on GitHub.
github.com
'CS > Data Structure' 카테고리의 다른 글
| [Data Structure] Hash (0) | 2024.04.03 |
|---|---|
| [Data Structure] B-Tree&B+Tree (0) | 2024.04.03 |
| [Data Structure] Tree (0) | 2024.03.31 |
| [Data Structure] Heap (0) | 2024.03.31 |
| [Data Structure] Queue (0) | 2024.03.31 |
