다익스트라 알고리즘?
- 그래프에서 최소 비용을 구하는 경우 사용되는 알고리즘
- 최소 비용 중, 주어진 두 노드(시작 노드, 도착 노드) 사이의 최소 비용인 경로를 찾을 때 유용하게 사용된다.
동작 원리
- 시작 노드와 직접적으로 연결된 모든 정점들의 거리를 비교해서 업데이트 시켜주고, 시작 노드를 방문한 노드로 체크한다.
- 방문한 정점들과 연결되어 있는 정점들 중, 비용이 적게드는 정점을 선택하고, 해당 정점을 방문한 정점으로 선택해준다.
- 2번 과정으로 갱신될 수 있는 정점들의 거리를 갱신시켜준다.
- 2번 과정과 3번 과정을 반복한다.

- 시작노드를 0번 노드로 가정
- dist 배열이 초기 INF로 초기화되어 있다고 생각한다.
- 1번 과정에 의해 0번 노드로 갈 수 있는 1번노드와 4번 노드, 5번 노드의 거리를 갱신
- 0번 노드를 방문한 노드로 체크 (형광색)
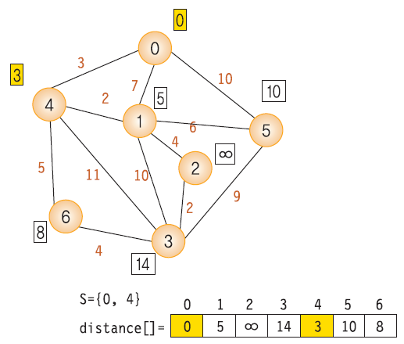
- 2번 과정에 의해 비용이 가장 적게드는 4번 노드를 선택하고 방문 표시해준다.
- 그후, 3번 과정에 의해 4번노드로 갈 수 있는 정점의 거리를 갱신한다.
- dist[1] = dist[3] + 2
- dist[3] = dist[4] + 11
- dist[6] = dist[4] + 5
- 이후, 4번 과정을 진행한다.

- 4번 노드에서 갈 수 있는 가장 비용이 적은 노드는 1번 노드가 된다.
- 3번 과정에 의해 정점의 거리를 갱신
알고리즘의 한계
- 다익스트라 알고리즘은 현재 선택된 정점들과 연결된 정점들중, 가장 비용이 적게드는 정점을 무조건적으로 방문했다고 체크한 후 연결된 다른 정점들의 값을 업데이트 시켜주었다.
- 이미 방문한 정점들은 방문 표시 후 다시는 값은 갱신하지 않는다.
- 다익스트라의 다신 방문하지 않는 특성으로 인해 가중치에 음수가 들어가면 이 알고리즘을 적용할 수 없다.
- 즉, 다익스트라 알고리즘은 모든 가중치가 양수인 경우 적용할 수 있다.
다익스트라 알고리즘 구현
void Dijkstra_Using_Heap(){
priority_queue<pair<int, int>> PQ;
PQ.push(make_pair(0, Start));
Dist[Start] = 0;
while (PQ.empty() == 0)
{
int Cost = -PQ.top().first;
int Cur = PQ.top().second;
PQ.pop();
for (int i = 0; i < Vertex[Cur].size(); i++)
{
int Next = Vertex[Cur][i].first;
int nCost = Vertex[Cur][i].second;
if (Dist[Next] > Cost + nCost)
{
Dist[Next] = Cost + nCost;
PQ.push(make_pair(-Dist[Next], Next));
}
}
}
for (int i = 1; i <= V; i++)
{
if (Dist[i] == INF)
cout << "INF" << endl;
else cout << Dist[i] << endl;
}
}
- queue에 값을 넣거나 뺄때 - 부호를 사용하는 이유는 최소힙을 구현하기 위해서다.
- 우선순위 큐를 일반적으로 사용하면 값이 클수록 더 높은 우선순위를 가지게된다.
- 따라서 값을 반전시켜 작은 값을 뽑는다.
출처
https://yabmoons.tistory.com/364
[ 다익스트라 알고리즘 ] 개념과 구현방법 (C++)
그래프 알고리즘에서 '최소 비용'을 구해야 하는 경우 사용할 수 있는 대표적인 알고리즘으로는'다익스트라 알고리즘' , '벨만-포드 알고리즘' , ' 플로이드 워샬 알고리즘' 이 있다.이번 글에서
yabmoons.tistory.com
'Algorithm' 카테고리의 다른 글
| [Algorithm] 최소 스패닝 트리 (0) | 2024.11.09 |
|---|---|
| [Algorithm] KMP 알고리즘 (0) | 2024.10.22 |
| <algorithm> 다익스트라(Dijkstra) 최단경로 알고리즘 (0) | 2024.02.24 |
| <algorithm> Red-Black Tree (RB Tree) (0) | 2024.01.26 |
| <algorithm> 그리디 알고리즘 (0) | 2023.11.22 |
