[게임수학] 수
수와 집합
- 게임을 구성하는 가상 세계를 이해하기 위한 첫걸음은 집합(set)이라는 개념으로 수를 이해하는것이다.
- 집합은 서로 구분이 되는 원소(Element)로 구성된 묶음을 의미한다.
- 수의 집합은 아래와 같이 구성된다.
- N (자연수) : 물건을 세거나 순서를 지정하기 위해 사용하는 수의 집합
- Z (정수) : 자연수와 자연수의 음수, 0을 포합하는 수의 집합
- Q (유리수) : 분모가 0이 아닌 두 정수의 비율 혹은 분수로 나타낼 수 있는 수의 집합
- I (무리수) : 두 정수 비 혹은 분수로 나타낼 수 없는 수의 집합
- C (복소수) : 실수와 제곱하면 -1이 되는 허수 단위 i를 조합해 a+bi(a, b는 실수) 형태로 표현하는 수의 집합
- H (사원수) : 실수와 제곱하면 -1이 되는 세 허수 단위 i,j,k 를 조합해 a+bi+cj+dk(a,b,c,d는 실수) 형태로 표현하는 수의 집합
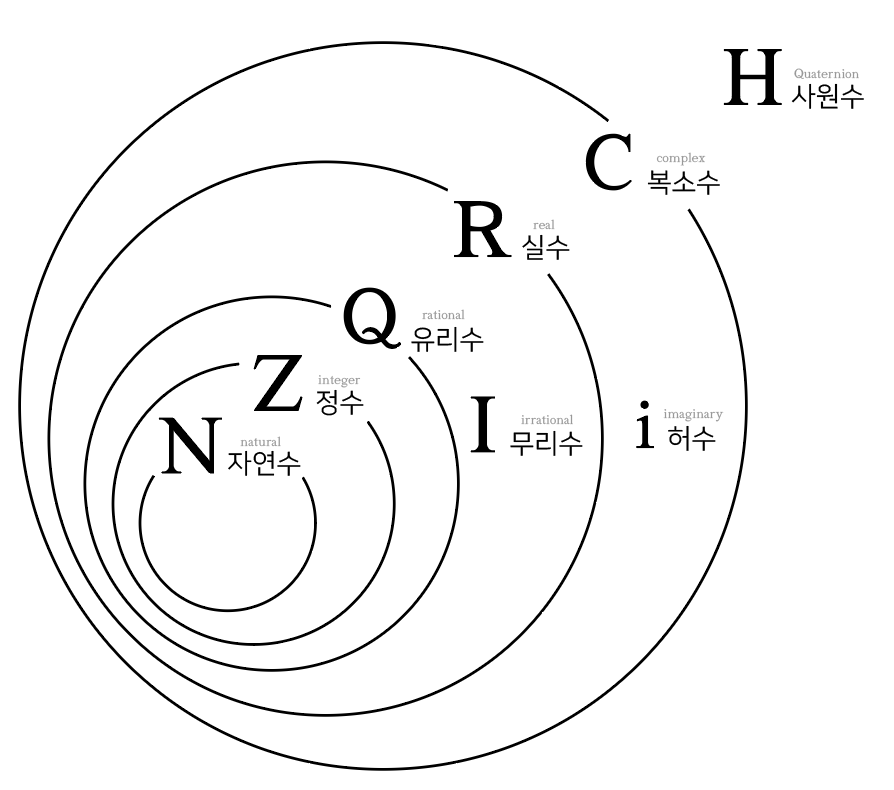
- 수집합의 관계는 위 그림과 같이 벤 다이어그램으로 도식화할 수 있다.
- 수를 이용해 가상 공간이라는 고차원 체계를 만들어야한다.
- 이를 위해 집합의 성질을 참과 거깃으로 명확하게 구분할 수 있는 명제가 필요함
- 명제 중에서 증명할 필요가 없는 기본 명제를 공리(Axiom)라고 한다.
- 공리를 기반으로 대상을 구분하는 집합론을 공리적 집합론(Axiomatic set theory)라고 한다.
- 공리적 집합론에서는 수가 가지는 연산에 대한 공리를 기반으로 수를 분류한다.
수의 연산
- 수 집합은 원소를 이용해 연산을 한다는 고유한 특징이 있다.
- 대표적인 연산으로는 덧셈, 뺄셈, 곱셈, 나눗셈의 사칙연산이 있다.
- 두 개의 원소를 사용해 새로운 원소를 만들어내기 때문에 이항연산(Binary Operation)이라고 부른다.
- 같은 집합에 속한 두 수를 투입한 이항연산의 결과가 항상 투입한 집합에 속하는 경우가 있다.
- 이러한 이항연산을 해당 집합에 닫혀있다(Closure)고 한다.
- 이항연산에는 아래와 같은 성질이 존재한다.
- 교환 법칙
- 결합 법칙
- 분배 법칙
- 항등원(identity)
- 역원(inverse)
교환 법칙
- 임의의 두 수 a와 b를 연산할 때 순서에 관계없이 항상 동일한 결과가 나오는 성질
a + b = b + a
a * b = b * a결합 법칙
- 연산이 두 번 이상 연속될 때, 앞의 연산을 먼저 계산한 결과와 뒤의 연산을 먼저 계산한 결과가 같은 성질
(a + b) + c = a + (b + c)
(a * b) * c = (a * b) * c분배 법칙
- 서로 다른 2가지 연산에 대해 좌분배법칙과 우분배법칙을 만족하면 분배법칙을 만족한다고 한다
a * (b + c) = a * b + a * c
(b + c) * a = b * a + c * aIdentity
- 임의의 수와의 연산 결과를 항상 동일한 수로 만들어주는 특별한 수
a + 0 = a //0: 덧셈의 항등원
a * 1 = a //1: 곱셈의 항등원Inverse
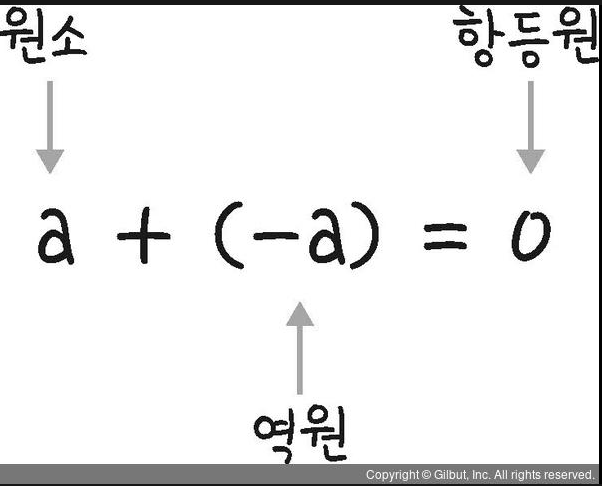
- 임의의 수와 연산 결과를 항상 항등원으로 만들어주는 특별한 수
a + (-a) = 0 //-a: a의 덧셈 역원 (반대수 Opposite number)
a * 1 / a = 1 //1/a: a의 곱셈 역원 (역수 Reciprocal)수의 구조
- 공리적 집합론에서 두 연산에 대해 아래와 같은 11개의 공리를 모두 만족하는 수의 집합을 체(Field)의 구조를 가진다고 표현한다.
- 연산에 대해 닫혀있다.
- 연산에 대해 결합 법칙이 성립한다.
- 연산에 대한 항등원이 존재한다.
- 연산에 대한 역원이 존재한다.
- 연산에 대해 교환 법칙이 성립한다.
- 두 번째 연산에 대해 닫혀 있다.
- 두 번째 연산에 대해 결합 법칙이 성립한다.
- 첫 번째 연산과 두 번째 연산에 대해 분배 법칙이 성립한다.
- 두 번째 연산에 대해 교환 법칙이 성립한다.
- 두 번째 연산에 대해 항등원이 존재한다.
- 두 번째 연산에 대해 역원이 존재한다. (0은 제외)
- 정수의 덧셈은 위 공리를 모두 만족한다.
- 정수의 뺄셈은 교환 법칙이 성립하지 않기 때문에 위 공리를 모두 만족하지 않는다.
- 정수 집합 Z에 곱셈 연산을 추가하고 살펴본다면 정수 집합은 곱셈에 닫혀 있고, 결합법칙과 분배법칙이 성립하며 교환법칙도 성립한다.
- 하지만 정수 집합의 원소 a에 대한 곱셈의 역원은 1/a인데 이는 정수가 아니기 때문에 11번의 공리를 만족하지 못한다.
- 덧셈에 대한 역원이 존재하지 않는 자연수(N)와 곱셈에 대한 역원이 존재하지 않는 정수(Z)는 11가지 공리를 만족하지 못한다.
- 하지만 유리수(Q), 실수(R)는 곱셈의 역원이 존재하기 때문에 덧셈과 곱셈 두 연산에 대해 11가지 공리를 모두 만족한다.
- 뺄셈과 나눗셈은 교환법칙을 만족하지 않기 때문에 체의 구조를 지니지 못한다.
- 뺄셈 대신 덧셈의 역원을 사용하고 나눗셈 대신 곱셈의 역원을 사용하면 되기 때문에 수 집합의 구조를 분석할 때는 덧셈과 곱셈의 두 가지 연산에 대해서만 살펴보는 것
수의 표현
- 체의 구조를 만족하는 수집합은 유리수(Q), 실수(R)가 있다.
- 직선 상에 유리수의 모든 원소를 순서대로 나열하는 상황을 가정한다면 무리수를 표현할 수 없기 때문에 빈틈이 생길것
- 이러한 빈틈을 무리수로 채워 완벽한 연속성을 가지는 직선을 만들어 내는 수가 실수(R)다.

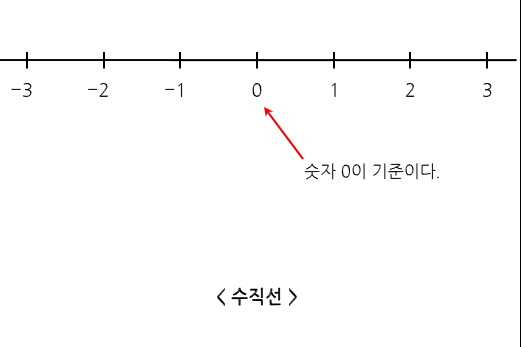
- 실수를 대응시켜 표현한 직선을 수직선(Number Line)이라하며 직각으로 만나는 직선을 의미하는 수직선(Perpendicular Line)과 같은 의미이다.

- 어떤 수의 원점으로부터의 거리는 수직 막대(Vertical Bar)기호를 써서 나타내는데 이를 절댓값(Absolute value)이라고 한다.

- 덧셈 연산은 점을 평행 이동시키는 작업으로 해석할 수 있다.
- -4와 -1의 합은 수의 위치를 왼쪽 방향으로 4칸만큼 이동시키는 작업
- 1과 2의 합은 오른쪽 방향으로 2칸 이동시키는 작업

- 곱셈은 원점을 기준으로 점의 위치를 지정된 배율만큼 늘리고 대칭시키는 작업으로 해석할 수 있다.
- 어떤 수와 2의 곱은 원점으로부터 거리를 같은 방향으로 2배 키우는 작업
- 왼쪽 항의 수가 가진 크기를 오른쪽 수가 가진 크기의 배율로 늘리거나 줄인 후 오른쪽 수의 부화가 양의 부호인 경우 원 방향을 유지하고, 음수인 경우 반대 방향으로 대칭시키는 작업
함수
- 함수(Function)란 두 집합에서 첫 번째 집합의 모든 원소가 빠짐없이 두 번째 집합의 어떤 원소로 대응하는 관계를 의미한다.
- 두 집합을 X와 Y라는 기호로 지정하고, 집합 X의 원소를 x, 집합 Y의 원소를 y라 할 때
- X에서 Y로 대응되는 함수를 y = f(x)로 나타낸다.
- 함수는 아래 규칙이 성립돼야 한다.
- 첫 번째 집합의 모든 원소에 대한 대응 관계가 존재해야 함
- 첫 번째 집합의 원소는 두 번째 집합의 한 원소에 대응되어야 함
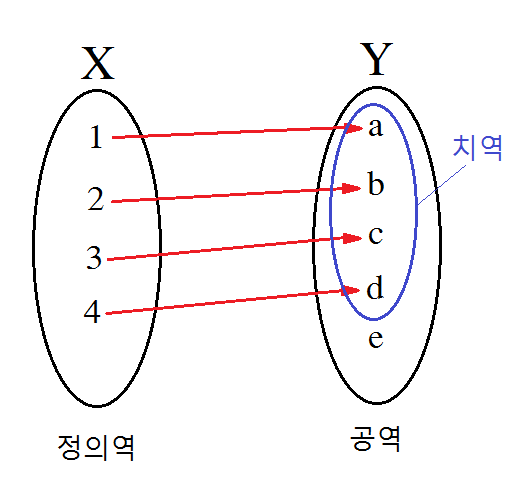
- 함수에서 첫 번째 집합을 정의역(Domain)이라고 하고, 두 번째 집합을 공역(Codomaion)이라 한다.
- 정의역에 대응되는 공역의 원소만 따로 모아 부분 집합(Subset)을 형성할 수 잇는데, 이를 치역(Range)이라고 부른다.
- 함수에 사용하는 정의역의 요소를 입력(Input), 입력에 대응하는 공역의 요소를 출력(Output)이라 한다.
함수의 종류
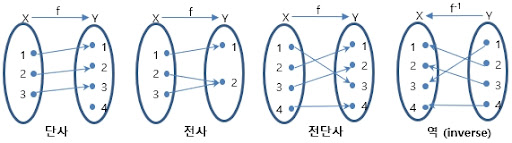
- 전사함수
- 전사함수(Surjection)는 공역의 모든 요소가 정의역에 대응되는 함수이다.
- 즉 공역와 치역이 동일한 함수다.
- 단사함수
- 단사함수(Injection)는 정의역과 공역의 요소가 일대일로 대응되는 함수이다.
- 정의역이 두 요소가 공역의 한 요소에 대응되는건 단사 함수가 아니다.
- 전단사함수
- 전단사함수(Bijection)는 정의역과 공역의 모든 요소가 빠짐없이 일대일로 대응되는 함수를 의미한다.
합성함수
- 2개의 함수를 연쇄적으로 이어서 하나의 함수로 만드는 연산을 함수의 합성(Function Composition)이라 한다.
- X,Y,Z 세 집합 사이에 두 함수 f(x)와 g(y)가 존재할 때
- 두 함수를 연쇄적으로 이어 합성함수를 만들면 중간에 위치한 집합 Y를 생략하고 집합 X와 Z의 직접적인 대응 관계를 표현할 수 있다.
- 이러한 합성함수는 g·f 혹은 g(f(x))로 표시
- 먼저 실행되는 함수 f가 (·)기호의 오른쪽에 놓인다는 점을 유의
- 합성함수 g·f는 g 써클 f로 부르는데, 대응 순서에 맞춰서 g 애프터 f 라고도 부른다.
항등함수와 역함수
- 정의역과 공역이 동일한 값으로 대응되는 함수를 항등함수(Identity Function)라고 하며 기호 id로 나타낸다.
- 항등함수는 연산의 항등원과 동일한 역할을 수행한다.
- 만약 합성함수를 사용해 함수에 연산의 개념을 도입하면 세 집합의 대응관계는 다음과 같이 표현된다.
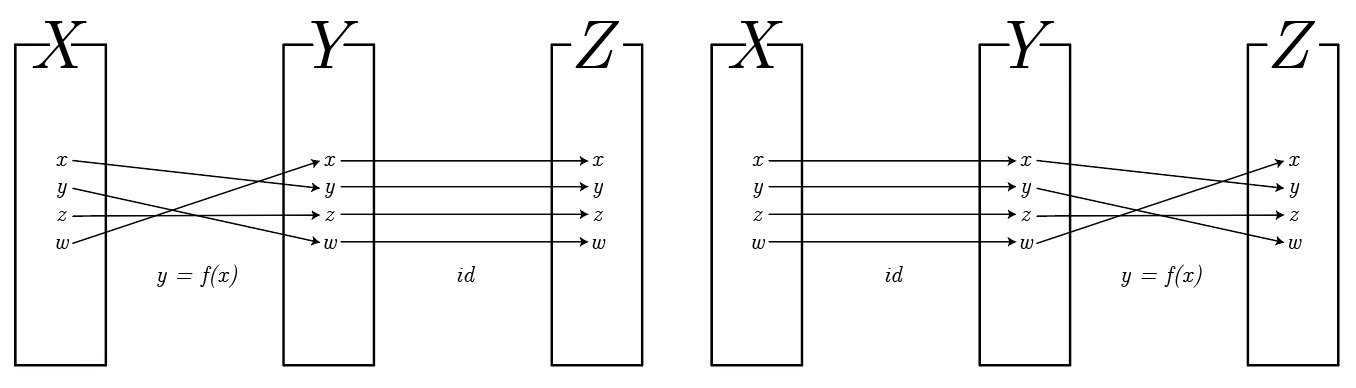
- 왼쪽 그림을 수식으로 나타내면 id · f = f이고 오른쪽을 수식으로 나타내면 f · id = f가 된다.
- 항등함수는 어느 위치에 있든지 합성의 결과는 원 함수와 동일한 대응 관계를 나타낸다.
- 역원 개념과 동일하게 합성함수의 대응 결과가 항등함수가 되는 경우
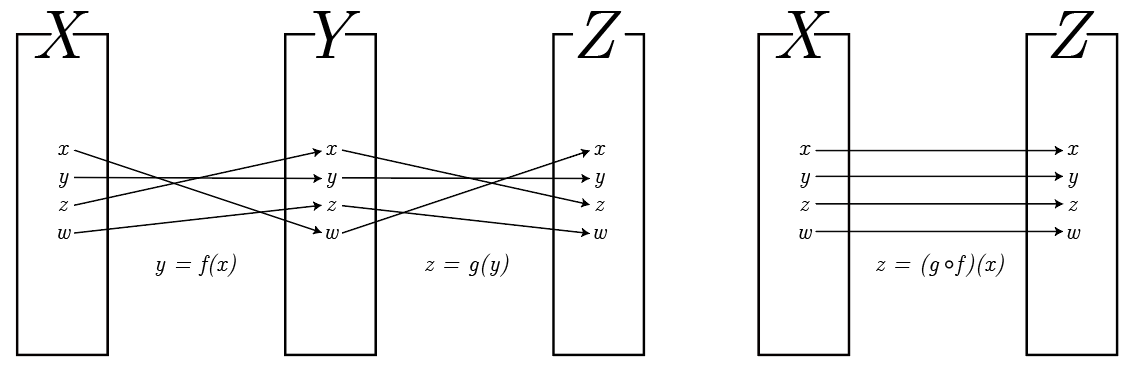
- 오른쪽 그림과 같은 대응 관계가 있다면, 이를 합성해 간추린 결과 오른쪽 그림과 같이 동일한 원소끼리 대응될 것
- 왼쪽 그림의 g(y)와 같은 함수를 역함수라고 한다.
- 역함수는 f^-1로 표기
- 어떤 함수와 역함수를 합성한 결과는 오른쪽 그림과 같이 언제나 항등함수가 된다.
- 항등함수는 다음의 수식을 만족한다.
f^-1 · f = id
f · f^-1 = id
(g · f)^-1 = f^-1 · g^-1곱집합
- 곱집합(Cartesian product)이란 두 집합의 원소를 순서쌍으로 묶은 원소의 집합을 의미
- 집합 A와 B의 곱집합은 A X B 라고 표현
- 곱집합의 요소는 각 집합의 원소 a와 b를 순서쌍으로 묶어 (a, b)와 같이 표현
- 두 실수집합의 곱집합 R X R을 구성하고 함수의 정의역으로 설정해 입력요소를 2개로 지정하였다면, 수의 이항연산을 함수로 표현할 수 있음
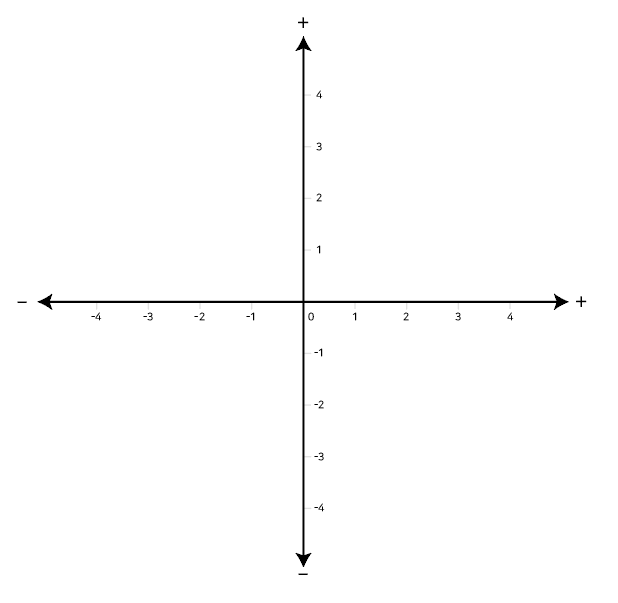
- 두 집합을 서로 수직으로 배치하는 곱집합의 성질을 응용하면
- 하나의 직선으로 표현한 실수집합 R을 확장해 두 실수의 집합의 곱집합 R X R을 좌표 평면으로 나타낼 수 있다.
- 다시 실수 집합을 곱집합으로 설정하면 3차원 공간이 된다.
출처
https://m.yes24.com/Goods/Detail/107025224
이득우의 게임 수학 - 예스24
39가지 실시간 렌더링 게임 프로그래밍 실습 예제를 하나씩 따라 해보며 독자가 직접 체득하는 흥미로운 게임 수학의 세계! 게임 개발자와 그래픽 아티스트들이 궁금해 했던 3D 가상 세계와 메타
m.yes24.com
https://wecandev.tistory.com/203
[이득우 게임수학] 2. 수 : 가상 세계를 구성하는 가장 작은 단위
수와 집합 의무 교육에서 배운 집합은 서로 구분이 되는 원소(Element)로 구성된 묶음을 의미한다. 소박한 집합론(Naive set theory)이라 한다. N (자연수) : 물건을 세거나 순서를 지정하기 위해 사용하
wecandev.tistory.com
https://velog.io/@thswl1230/%EA%B2%8C%EC%9E%84%EC%88%98%ED%95%99-%EC%88%98
[게임수학] - 수
2장. 수: 가상 세계를 구성하는 가장 작은 단위2.1 수와 집합게임을 구성하는 가상 세계를 이해하기 위한 첫걸음은 집합(set) 이라는 개념으로 수를 이해하는것이다.어릴때 배운 집합은 서로 구분
velog.io
https://walll4542developer.github.io/math/Numbers-and-Set/
게임 수학 입문 01 - 수와 집합(Numbers and Set)
게임을 구성하는 가상 세계를 이해하기 위한 첫 걸음은 집합(Set)이라는 개념으로 수를 이해하는 것입니다. 집합이란 서로 구분되는 원소(Element)로 구성된 묶음을 의미합니다. 이러한 집합론을
walll4542developer.github.io
https://walll4542developer.github.io/math/Function/
게임 수학 입문 02 - 함수(Function)
함수(Function)란 두 집합에서 첫 번째 집합의 모든 원소가 빠짐없이 두 번째 집합의 어떤 원소에 대응하는 관계를 의미합니다. 두 집합을 각각 X와 Y라는 기호로 지정하고, 집합 X의 원소를 x, 집합
walll4542developer.github.io