CS/Data Structure
[Data Structure] Queue
hanseongbugi
2024. 3. 31. 16:38
Queue(큐)?
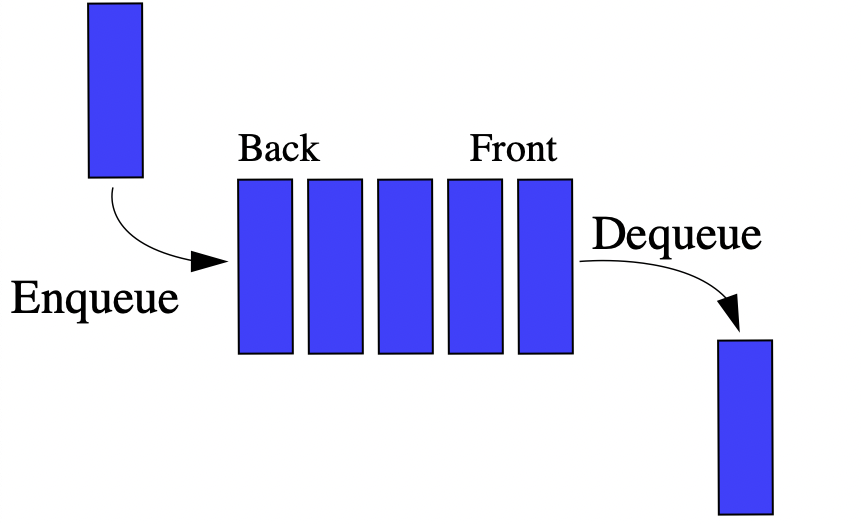
- 큐 자료구조는 스택과 다르게 선입선출(FIFO)의 구조를 가지고 있다.
- queue는 사전적으로 대기줄을 뜻한다.
- 입력과 출력을 한 쪽 끝(front, rear)으로 제한한다.
Queue의 활용
- 버퍼
- 마구 입력된 것을 처리하지 못하고 있는 상황
- BFS
- 데크(Deque), 우선순위 큐(Priority Queue) 등으로 변형
- 캐시 구현
- 어떠한 작업/데이터를 순서대로 실행/사용하기 위해 대기
Queue의 연산자
- 큐의 가장 첫 원소를 front, 끝 원소를 rear라고 부름
- 큐는 들어올 때 rear로 들어오지만, 나올 때는 front부터 빠지는 특성을 가짐
- 접근방법은 가장 첫 원소와 끝 원소로만 가능
| enQueue() | 데이터 넣음 |
| deQueue() | 데이터 뺌 |
| isEmpty() | 비어있는 지 확인 |
| isFull() | 꽉차있는 지 확인 |
- 데이터를 넣고 뺄 때 해당 값의 위치를 기억해야 함.
- 스택에서 스택 포인터와 같은 역할
- 이 위치를 기억하고 있는 게 front와 rear
- front
- deQueue 할 위치 기억
- rear
- enQueue 할 위치 기억
Queue 구현
기본 구조
template<typename T>
class Queue{
private:
int size = 0;
int rear = -1;
int front = -1;
T* queue;
public:
Queue(int size){
this->size = size;
queue = new T[size];
};
~Queue(){
delete[] queue;
}
void enQueue(const T& value);
T deQueue(const T& value);
bool isEmpty();
bool isFull();
};enQueue
template<typename T>
void Queue<T>::enQueue(const T& value){
if(isFull()){
return;
}
queue[++rear] = value;
}- enQueue 시, 가득 찼다면 꽉 차 있는 상태에서 enQueue를 했기 때문에 overflow
- 아니면 rear에 값 넣고 1 증가
deQueue
template<typename T>
T Queue<T>::deQueue(const T& value){
if(isEmpty()){
return NULL;
}
T data = queue[front];
queue[front++] = NULL;
return data;
}- deQueue를 할 때 공백이면 underflow
- front에 위치한 값에 있는 data를 꺼낸 후, 꺼낸 위치는 NULL로 채워줌
isEmpty
template<typename T>
bool Queue<T>::isEmpty(){
return front==rear;
}- front와 rear가 같아지면 비어진 것
isFull
template<typename T>
bool Queue<T>::isFull(){
return (rear == size-1);
}- rear가 사이즈-1과 같아지면 가득찬 것
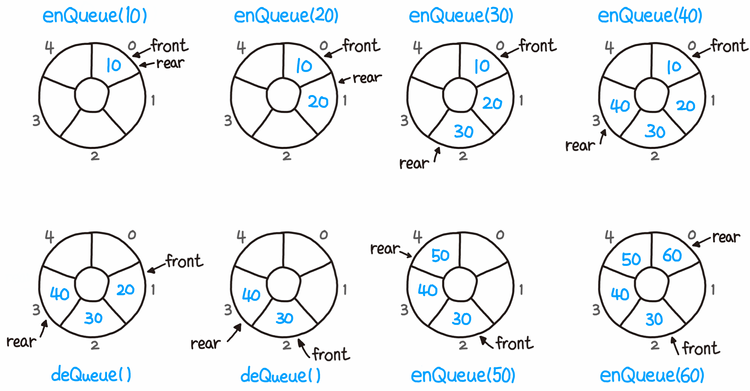
원형 큐
- 일반 큐의 단점
- 큐에 빈 메모리가 남아 있어도, 꽉 차있는것으로 판단할 수도 있음
- rear가 끝에 도달하였을 때
- 일반 큐의 단점을 개선한 것이 원형 큐
- 논리적으로 배열의 처음과 끝이 연결되어 있는 것으로 간주함
- 원형 큐는 초기 공백 상태일 때 front와 rear가 0
- 공백, 포화 상태를 쉽게 구분하기 위해 자리 하나를 항상 비워둠
(index + 1) % size로 순환시킨다기본 구조
template<typename T>
class Queue{
private:
int size = 0;
int rear = 0;
int front = 0;
T* queue;
public:
Queue(int size){
this->size = size;
queue = new T[size];
};
~Queue(){
delete[] queue;
}
void enQueue(const T& value);
T deQueue(const T& value);
bool isEmpty();
bool isFull();
};enQueue
template<typename T>
void Queue<T>::enQueue(const T& value){
if(isFull()){
return;
}
rear = (++rear) % size;
queue[rear] = value;
}- enQueue 시, 가득 찼다면 꽉 차 있는 상태에서 enQueue를 했기 때문에 overflow
deQueue
template<typename T>
T Queue<T>::deQueue(const T& value){
if(isEmpty()){
return NULL;
}
front = (++front) % size;
T data = queue[front];
return data;
}- deQueue를 할 때 공백이면 underflow
isEmpty
template<typename T>
bool Queue<T>::isEmpty(){
return front==rear;
}- front와 rear가 같아지면 비어진 것
isFull
template<typename T>
bool Queue<T>::isFull(){
return ((rear + 1) % size == front);
}- rear+1%size가 front와 같으면 가득찬 것
연결리스트로 구현한 Queue
- 원형 큐의 단점
- 메모리 공간은 잘 활용하지만, 배열로 구현되어 있기 때문에 큐의 크기가 제한
- 원형 큐의 단점을 개선한 것이 연결리스트 큐
- 연결리스트 큐는 크기가 제한이 없고 삽입, 삭제가 편리
- 삽입은 tail, 제거는 head로 하면서 삽입/삭제를 스택처럼 O(1)에 가능하도록 구현이 가능하다.
기본 구조
template <typename T>
class Node
{
public:
T data;
Node* next;
Node() :data(0), next(nullptr) {};
};
template <typename T>
class Queue
{
private:
Node<T>* head;
Node<T>* tail;
public:
Queue() :head(nullptr), tail(nullptr) {};
void enQueue(T item);
T deQueue();
bool isEmpty();
};enQueue
template<typename T>
void Queue<T>::enQueue(T item)
{
Node<T>* newNode = new Node<T>;
newNode->data = item;
if (head == nullptr)
{
head = newNode;
tail = newNode;
}
else
{
tail->next = newNode;
tail = tail->next;
}
}- 데이터 추가는 끝 부분인 tail에 한다.
- 큐가 비어있다면(head가 NULL을 가리키고 있다면) head와 tail을 새로 생성한 노드를 가리키게 한다.
- 큐가 비어있지 않다면 기존 tail의 next에 새로 생성한 node를 가리키게 하고 tail을 변경한다.
deQueue
template<typename T>
T Queue<T>::deQueue()
{
if (isEmpty())
return -1;
else
{
Node<T>* ptr = head;
T vaule = head->data;
if (head == tail)
{
head =nullptr;
tail= nullptr;
delete(head);
}
else
{
ptr = ptr->next;
delete(head);
head = ptr;
}
return vaule;
}
}- 데이터는 head를 통해 꺼낸다.
- 가장 먼저 들어온 것 부터 빼야하므로
- head의 데이터를 미리 저장해둔다.
- 기존의 head의 다음 노드를 head로 설정한다.
- 저장해둔 데이터를 반환한다.
전체 소스코드
#include <iostream>
using namespace std;
template <typename T>
class Node
{
public:
T data;
Node* next;
Node() :data(0), next(nullptr) {};
};
template <typename T>
class Queue
{
private:
Node<T>* head;
Node<T>* tail;
public:
Queue() :head(nullptr), tail(nullptr) {};
void enQueue(T item);
T deQueue();
bool isEmpty();
};
template<typename T>
void Queue<T>::enQueue(T item)
{
Node<T>* newNode = new Node<T>;
newNode->data = item;
if (head == nullptr)
{
head = newNode;
tail = newNode;
}
else
{
tail->next = newNode;
tail = tail->next;
}
}
template<typename T>
T Queue<T>::deQueue()
{
if (isEmpty())
return -1;
else
{
Node<T>* ptr = head;
T vaule = head->data;
if (head == tail)
{
head =nullptr;
tail= nullptr;
delete(head);
}
else
{
ptr = ptr->next;
delete(head);
head = ptr;
}
return vaule;
}
}
template<typename T>
bool Queue<T>::isEmpty()
{
if (tail == nullptr)
return true;
else
return false;
}
출처
C++ 링크드 리스트를 이용한 큐 구현 (Single Linked List Queue C++)
FILO(LILO)구조 구현한 함수(다형성을 위해 템플릿 사용) void Enqueue(T _value); T Dequeue(); 가장 먼져 들어간 값을 반환하고 큐에서 지움 bool empty(); 비어있는지 확인하는 함수 /* 싱글링크드 리스트를 이
xtar.tistory.com
https://github.com/gyoogle/tech-interview-for-developer
GitHub - gyoogle/tech-interview-for-developer: 👶🏻 신입 개발자 전공 지식 & 기술 면접 백과사전 📖
👶🏻 신입 개발자 전공 지식 & 기술 면접 백과사전 📖. Contribute to gyoogle/tech-interview-for-developer development by creating an account on GitHub.
github.com
https://velog.io/@hysong/%EC%9E%90%EB%A3%8C%EA%B5%AC%EC%A1%B0-%ED%81%90Queue
[자료구조] 큐(Queue)
큐(Queue)는 먼저 추가한 데이터를 먼저 반환/삭제하는 선입선출(FIFO - First In First Out) 형식의 선형 또는 원형 자료구조이다.
velog.io