너비 우선 탐색(BFS, Breadth-First Search)
- 시작 정점으로부터 가까운 정점을 먼저 방문하고 멀리 떨어져 있는 정점을 나중에 방문하는 순회 방법
- 큐를 사용하여 구현됨
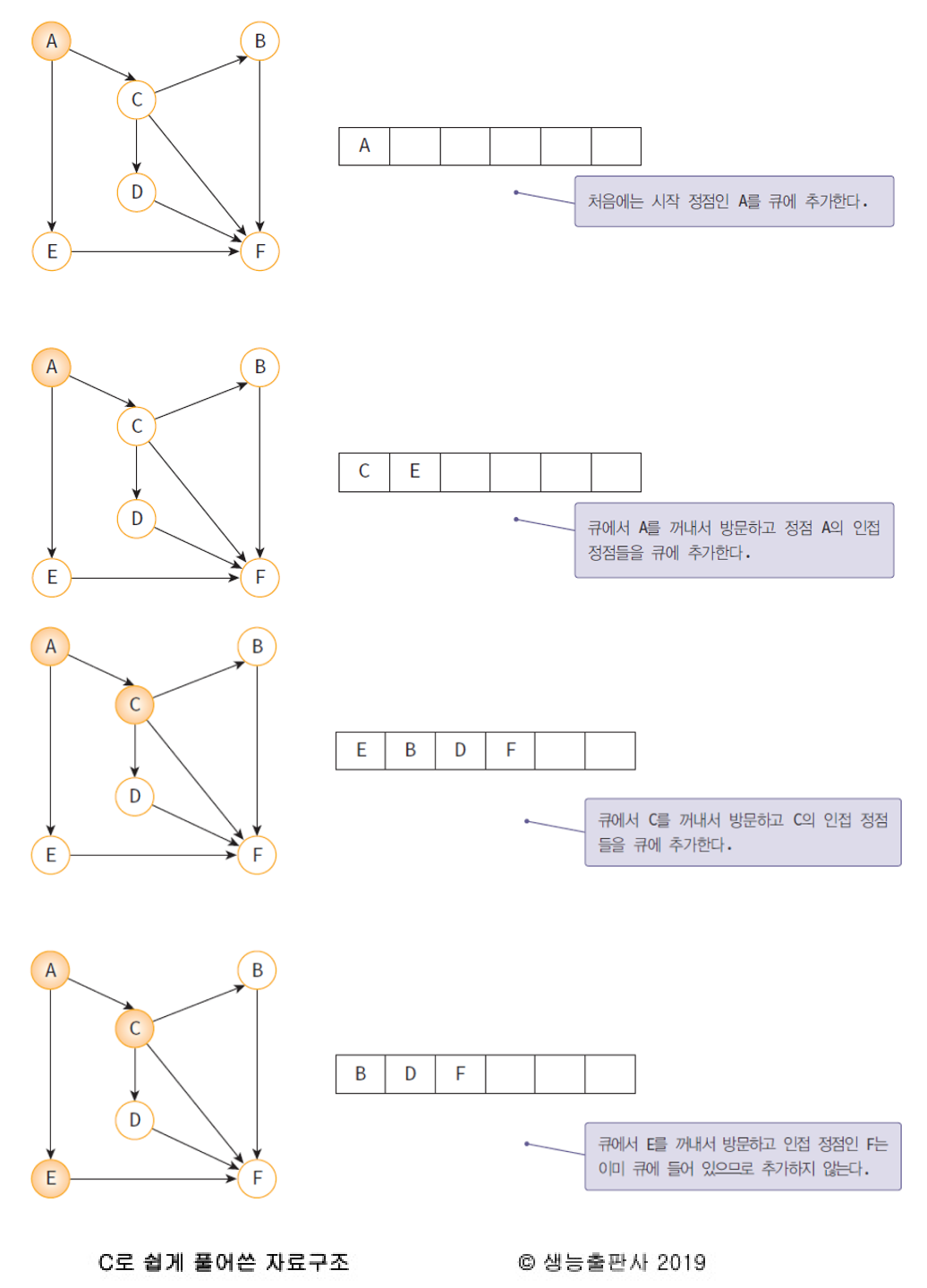
- A 노드(시작 노드)를 방문한다. (방문한 노드 체크)
- 큐에 방문된 노드를 삽입(enqueue)한다.
- 초기 상태의 큐에는 시작 노드만이 저장 (초기 큐에서는 시작 노드만 있음)
- 즉, A 노드의 이웃 노드를 모두 방문한 다음에 이웃의 이웃들을 방문한다. - 큐에서 꺼낸 노드과 인접한 노드들을 모두 차례로 방문한다.
- 큐에서 꺼낸 노드를 방문한다. (큐에서 값을 빼서 탐색 시작)
- 큐에서 커낸 노드과 인접한 노드들을 모두 방문한다.
- 인접한 노드가 없다면 큐의 앞에서 노드를 꺼낸다(dequeue).
- 큐에 방문된 노드를 삽입(enqueue)한다. - 큐가 소진될 때까지 계속한다.
breadth_first_search(v):
v를 방문되었다고 표시;
큐 Q에 정점 v를 삽입;
while (Q가 공백이 아니면) do
Q에서 정점 w를 삭제;
for all u ∈ (w에 인접한 정점) do
if (u가 아직 방문되지 않았으면)
then u를 큐에 삽입;
u를 방문되었다고 표시;
C++ 코드
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
bool visited[9];
vector<int> graph[9];
// BFS 함수 정의
void bfs(int start) {
queue<int> q;
q.push(start); // 첫 노드를 queue에 삽입
visited[start] = true; // 첫 노드를 방문 처리
// 큐가 빌 때까지 반복
while (!q.empty()) {
// 큐에서 하나의 원소를 뽑아 출력
int x = q.front();
q.pop();
cout << x << ' ';
// 해당 원소와 연결된, 아직 방문하지 않은 원소들을 큐에 삽입
for (int i = 0; i < graph[x].size(); i++) {
int y = graph[x][i];
if (!visited[y]) {
q.push(y);
visited[y] = true;
}
}
}
}
int main(void) {
// 노드 1에 연결된 노드 정보 저장
graph[1].push_back(2);
graph[1].push_back(3);
graph[1].push_back(8);
// 노드 2에 연결된 노드 정보 저장
graph[2].push_back(1);
graph[2].push_back(7);
// 노드 3에 연결된 노드 정보 저장
graph[3].push_back(1);
graph[3].push_back(4);
graph[3].push_back(5);
// 노드 4에 연결된 노드 정보 저장
graph[4].push_back(3);
graph[4].push_back(5);
// 노드 5에 연결된 노드 정보 저장
graph[5].push_back(3);
graph[5].push_back(4);
// 노드 6에 연결된 노드 정보 저장
graph[6].push_back(7);
// 노드 7에 연결된 노드 정보 저장
graph[7].push_back(2);
graph[7].push_back(6);
graph[7].push_back(8);
// 노드 8에 연결된 노드 정보 저장
graph[8].push_back(1);
graph[8].push_back(7);
bfs(1);
}출력
1 2 3 8 7 4 5 6
너비 우선 탐색(BFS)의 시간 복잡도
- 인접 리스트로 표현된 그래프: O(N+E)
- 인접 행렬로 표현된 그래프: O(N^2)
'Algorithm' 카테고리의 다른 글
| <algorithm> Red-Black Tree (RB Tree) (0) | 2024.01.26 |
|---|---|
| <algorithm> 그리디 알고리즘 (1) | 2023.11.22 |
| <algorithm> Dynamic Programming (1) | 2023.11.06 |
| <algorithm> 깊이 우선 탐색(DFS) (1) | 2023.10.24 |
| <algorithm> 이진 탐색 (1) | 2023.10.05 |
